Menge
Nicht-axiomatische Mengenlehre
![]()
Richard Dedekind schrieb 1887, dass es sehr häufig vorkommt, „daß verschiedene Dinge a, b, c ... aus irgendeiner Veranlassung unter einem gemeinsamen Gesichtspunkte aufgefaßt, im Geiste zusammengestellt werden, und man sagt dann, daß sie ein System S bilden; man nennt die Dinge a, b, c ... die Elemente des Systems, sie sind enthalten in S; umgekehrt besteht S aus diesen Elementen. Ein solches System S (oder ein Inbegriff, eine Mannigfaltigkeit, eine Gesamtheit) ist als Gegenstand unseres Denkens ebenfalls ein Ding; es ist vollständig bestimmt, wenn von jedem Ding bestimmt ist, ob es Element von S ist oder nicht.“ (Dedekind: Was sind und was sollen die Zahlen? §1 Systeme von Elementen, Ziffer 2).
1895 formulierte Georg Cantor: „Unter einer ‚Menge‛ verstehen wir jede Zusammenfassung M von bestimmten wohlunterschiedenen Objecten m unserer Anschauung oder unseres Denkens (welche die ‚Elemente‛ von M genannt werden) zu einem Ganzen.“ (Math. Annalen Bd. 46, S. 481). Oder mit den Worten von Felix Hausdorff (1868−1942): „Eine Menge entsteht durch Zusammenfassung von Einzeldingen zu einem Ganzen. Eine Menge ist eine Vielheit, als Einheit gedacht.“ (Hausdorff: Mengenlehre, Walter de Gruyter & Co. 19353, S. 11).
Während bei Dedekind grundsätzlich irgendwelche Dinge zu einem System zusammengefasst werden können, darf man laut Cantor nur bestimmte Objekte zu einer Menge zusammenfassen. Am 28. Juli 1899 schrieb Cantor demgemäß in einem Brief an Dedekind: „Eine Vielheit kann nämlich so beschaffen sein, daß die Annahme eines ‚Zusammenseins‛ aller ihrer Elemente auf einen Widerspruch führt, so daß es unmöglich ist, die Vielheit als eine Einheit, als ‚ein fertiges Ding‛ aufzufassen. ... Wie man sich leicht überzeugt, ist z.B. der ‚Inbegriff alles Denkbaren‛ eine solche Vielheit.“
Auch die Vielheit aller Mengen, heute „Allklasse“ genannt, ist keine Menge (vgl. den folgenden Abschnitt: Widersprüche!). Um diese Aussage zu verstehen, muss man garnicht wissen, was eine Menge „eigentlich“ ist. Man postuliert vielmehr die Existenz von Mengen und die Gültigkeit formaler Regeln, die im Mengenuniversum gelten sollen und kann dann beweisen, dass die Allklasse diesen Regeln nicht gehorcht (→ Zermelo-Fraenkel’sches Axiomensystem).
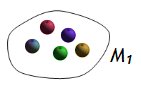
In naiver Weise können Mengen auf verschiedene Weise dargestellt werden: eine Menge verschiedenfarbiger Kugeln etwa durch ein Bild,
die Menge aller Primzahlen zwischen 0 und 20 in aufzählender Form,
M2 = { 2, 3, 5, 7, 11, 13, 17, 19 }
oder die Menge bestimmter Objekte durch deren Eigenschaft:
M3 = { x ∈∈ M2 | x < 10 }.
In der Menge M3 sind all diejenigen Elemente aus M2 enthalten, die kleiner als 10 sind.
Ist x ein Element einer Menge M, so schreibt man „x ∈∈ M“. Ist x nicht Element einer Menge M, so schreibt man „x ∉∉ M“. Die Menge { }, die keine Elemente hat, heißt leere Menge.
Seien nun M und N zwei nichtleere Mengen. Wenn x ∈∈ N
aus x ∈∈ M folgt, so
schreibt man „M ⊆ N“
(„M ist
Teilmenge von N“). Kurz formuliert:
(x ∈∈ M ⇒ x ∈∈ N) ⇔def M
⊆ N
Sei M ⊆ N.
Wenn es ein Objekt x gibt mit x ∈∈ N
und x ∉∉ M,
so ist M eine echte Teilmenge von N und
man kann in diesem Fall schreiben: „M ⊂ N“.
Bezüglich „⊆“ gelten die folgenden Gesetze:
(I) A ⊆ A
(Reflexivitätsgesetz)
(II) (A ⊆ B
und B ⊆ A) ⇒ A = B (Identitätsgesetz)
(III) (A ⊆ B
und B ⊆ C) ⇒ A ⊆ C (Transitivitätsgesetz)
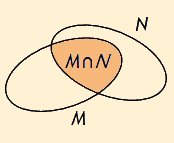
M ∩ N =def
{ x | x ∈∈ M und x ∈∈ N }
heißt Durchschnitt von M und N.
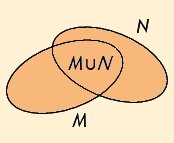
M ∪ N =def
{ x | x ∈∈ M
oder x ∈∈ N }
heißt Vereinigung von M und N.
Venn-Diagramme veranschaulichen diese Definitionen:
M und N heißen disjunkt genau dann, wenn M und N kein gemeinsames Element besitzen. Es gilt in diesem Fall also:
M ∩ N = { }.
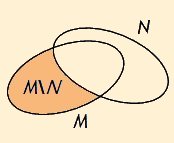
M\N =def
{ x | x ∈∈ M und x ∉∉ N } heißt Differenz von M und N.
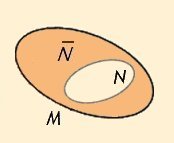
Ist N ⊆ M, so heißt
M\N Komplement von
N bezüglich M und wird mit „N“
bezeichnet.
Sämtliche Teilmengen einer Menge M bilden zusammen die Potenzmenge von M:
℘(M) =def
{ T | T ⊆ M }
Die Bedeutung der logischen Junktoren nicht, und, oder, wenn...so und genau dann,wenn, die in den vorstehenden Definitionen verwendet worden sind, muss noch erklärt werden. Am übersichtlichsten gelingt dies mit Hilfe der folgenden Verknüpfungstafeln. Hierbei sind "p" und "q" logische Aussagen; das Symbol „⊤“ steht für „wahr“, das Symbol „⊥“ steht für „falsch“. "p ˄ q" bedeutet "p und q"; "p ˅ q" bedeutet "p oder q"; "p → q" bedeutet "wenn p, so q"; "p ↔ q" bedeutet "p genau dann, wenn q" oder "p dann und nur dann, wenn q".
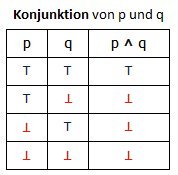
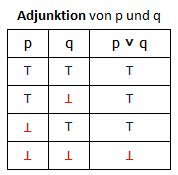
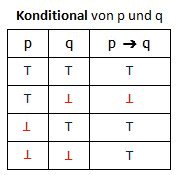
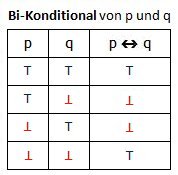
Das logische oder wird also nicht (wie in der Umgangssprache) im ausschließenden Sinne verwendet: "p oder q" ist dann und nur dann falsch, wenn sowohl "p" als auch "q" falsche Aussagen sind. Die Konditionalaussage "wenn p, so q" ist genau dann falsch, wenn "p" wahr, aber "q" falsch ist. Die Aussage "nicht p" ist falsch, wenn "p" wahr ist und wahr, wenn "p" falsch ist.
Folgt aus einer wahren mathematischen Aussage "a" eine andere wahre Aussage "b", dann schreibt man oft abkürzend „a ⇒ b“. Gilt "a ⇒ b und b ⇒ a", so sind die Aussagen "a" und "b" äquivalent und man schreibt „a ⇔ b“. Beispielsweise ist die Aussage
"(p ⇒ q) ⇔ (q ⇒ p)"
wahr, was man sich anhand folgender Verknüpfungstafel klarmacht. Hierbei bedeutet "p" die
Negation von "p", also "nicht p", ebenso ist "q" = "nicht q".

Sei nun M eine Menge und A, B und C beliebige Teilmengen von
M, das heißt A,B,C ∈∈ ℘(M). Dann sind A∩B,
A∪B und A ebenfalls Elemente von
℘(M) (man sagt:
℘(M) ist in Bezug auf die Mengenoperationen „∩“,
„∪“ und in Bezug auf die Komplementbildung abgeschlossen) und es gelten die folgenden Gesetze:
| (i) Idempotenzgesetze: |
A ∩ A = A
und A ∪ A = A |
| (ii) Kommutativgesetze: |
A ∩ B = B ∩ A
und A ∪ B = B ∪ A |
| (iii) Assoziativgesetze: |
A ∩ (B ∩ C) = (A ∩ B) ∩ C
A ∪ (B ∪ C) = (A ∪ B)
∪ C |
| (iv) Distributivgesetze: |
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) |
| (v) de Morgan’sche Gesetze: |
A ∩ B = A ∪ BA ∪ B = A ∩ B |
| (vi) Absorptionsgesetze: |
A ∩ (A ∪ B) = AA ∪ (A ∩ B) = A |
| (vii) Komplementgesetze: |
A ∩ A = { } und A
∪ A = M |
(viii) M = { } und { } = M |
(ix) B = A ⇒ B = A |
(x) { } ∈∈ ℘(M) |
Beweis:
Man überzeugt sich von der Gültigkeit dieser Gesetze auf rein logischem
Wege mit Hilfe von Verknüpfungstafeln. Sei mit „a“ die Aussage "x∈∈A"
bezeichnet, mit „ab“ die Aussage "x∈∈A und x∈∈B",
mit „avb“ die Aussage "x∈∈A oder x∈∈B",
und so fort. Die beispielsweise zum ersten Distributivgesetz gehörende Verknüpfungstafel sieht wie folgt aus
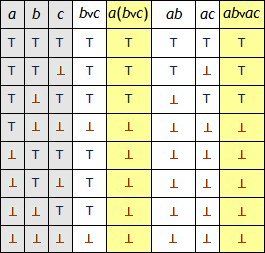
und man erkennt an den gelb unterlegten Spalten, dass
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
Die Aussage (x) sieht auf den ersten Blick merkwürdig aus. Sie besagt in Worten, dass die leere Menge Teilmenge von jeder Menge M ist, das
heißt: wenn x ∈∈ { },
so x ∈∈ M.
Die Aussage "x ∈∈ { }" ist jedoch
immer falsch, und deswegen ist die gesamte Konditionalaussage wahr (vgl. oben die entsprechende Verknüpfungstafel)!
Eine Veranschaulichung der Distributibutivgesetze durch Venn-Diagramme findet sich hier.
Wenn gewisse Objekte x eine gemeinsame Eigenschaft E haben,
liegt es nahe, diese Objekte zu einer Menge zusammenzufassen: ME =def { x | E trifft zu auf x }. Diesen Vorgang
der Mengenbildung nennt man Komprehension. Das sogenannte
Komprehensionsprinzip besagt, dass man diese Art der Mengenbildung
immer vornehmen kann, und zwar unabhängig sowohl von der Art der
betrachteten Objekte als auch von zumindest logisch formulierten
Eigenschaften. Der oben vorgestellten, meist „naiv“ genannten Mengenlehre
liegt insbesondere dieses Komprehensionsprinzip zugrunde.
Bertrand Russell hatte zu Beginn des vorigen Jahrhunderts die Idee zu der folgenden Komprehension: Man betrachte
alle Objekte, die die gemeinsame Eigenschaft besitzen, eine Menge zu sein. Diese Objekte bilden dann eine neue Menge, nämlich die
Menge aller Mengen: M = { m | m ist eine Menge }.
Aufgrund der Definition von M folgt sofort: M ∈∈ M, das heißt, es gibt
(mindestens) eine Menge, die sich selbst als Element enthält.
Sei nun die Russel’sche Menge M* definiert durch M* =def { m | m ist eine Menge und m ∉∉ m }.
Mit der Annahme, dass M* ∈∈ M*, folgt sofort aufgrund der
Definition von M*: M* ∉∉ M*,
ein Widerspruch zur Annahme! Nimmt man umgekehrt an, dass M* ∉∉ M*,
so ergibt sich aus der Definition von M*: M* ist keine Menge
oder M* ∈∈ M*.
Da aber M* als Menge vorausgesetzt war, folgt M* ∈∈ M*.
Wieder ein Widerspruch zur Annahme! Insgesamt hat man also das
Ergebnis, dass weder M* ∈∈ M*
noch M* ∉∉ M*
gilt oder aber - je nach Betrachtungsweise - M* ∈∈ M* ⇔ M* ∉∉ M*:
ein Resultat, aus dem zwingend folgt, dass M* keine Menge ist. Diese so genannte
Russell’sche Antinomie hat
zu der Erkenntnis geführt, dass es nicht gestattet sein darf, gemäß des
Komprehensionsprinzips in uneingeschränkter Weise Mengen zu bilden! Die Annahme, die der Russell’schen Antinomie
(, die - nebenbei bemerkt - unabhängig von Russell auch Zermelo entdeckt hat
und möglicherweise Cantor bereits bekannt war) zugrunde liegt, nämlich die
Existenz der Menge aller Mengen, ist offenbar falsch. Die Gesamtheit aller Mengen ist keine Menge!
Widersprüche ganz anderer Art ergeben sich bei unterschiedlicher Anordnung der Elemente unendlicher Mengen. Werden beispielsweise alle natürlichen
Zahlen (also die Elemente der Menge ℕ)
bezüglich „<“ angeordnet, 0 < 1 < 2 < 3 < ....,
dann sieht man anschaulich, dass man alle natürlichen Zahlen der Reihe nach
abzählen kann. Die Menge ℕ = { 0, 1, 2, ... } ist abzählbar unendlich.
Die Menge aller geraden natürlichen Zahlen ℕg = { 0, 2, 4, ... }
ist, genauso wie die Menge aller ungeraden natürlichen Zahlen
ℕu = { 1, 3, 5, ... },
ebenfalls abzählbar unendlich. Offensichtlich gilt
ℕ = ℕg ∪ ℕu = { 0, 2, 4, ..., 1, 3, 5, ... }.
Ist nun ℕ gleichzeitig abzählbar unendlich
und doppelt abzählbar unendlich? Es geht noch schlimmer: Sei mit
ℕp = { p, 2p, 3p, ...}
die Menge aller Vielfachen einer Primzahl p definiert, dann ist auch
ℕp abzählbar unendlich und die Menge
ℕ3 ∪ ℕ5 ∪ ℕ7 ∪ ....
= { 3, 6, 9, ..., 5, 10, 15, ... }
unendlich mal abzählbar unendlich, aber gleichzeitig weniger mächtig als ℕ, da unendlich viele Elemente, nämlich 0, 1, 2, 4, 8, 16, ... fehlen!?
In diesem Zusammenhang passt eine Diskussion über Quadratzahlen zwischen Salviati, Sagredo und Simplicio (Galileo Galilei: Unterredungen und mathematische Demonstrationen 1638, Erster Tag): Salviati erinnert daran, dass eine Quadratzahl aus der Multiplikation einer beliebigen Zahl mit sich selbst entsteht, diejenigen Zahlen, welche mit sich selbst multipliziert werden, Wurzeln genannt werden, und die anderen Zahlen, welche nicht aus zwei gleichen Faktoren bestehen, Nichtquadratzahlen heißen. (Mit „Zahlen“ sind hier die natürlichen Zahlen gemeint.) Das Gespräch verläuft dann so:
Salv. ...Wenn ich nun sage,
alle Zahlen, Quadrat- und Nichtquadratzahlen zusammen, sind mehr, als die Quadratzahlen allein, so ist das doch eine durchaus richtige Behauptung; nicht?
Simpl. Dem kann ich nicht widersprechen.
Salv. Frage ich nun, wieviel Quadratzahlen es giebt, so kann man in Wahrheit antworten, eben soviel als es Wurzeln giebt, denn
jedes Quadrat hat eine Wurzel, jede Wurzel hat ihr Quadrat, kein Quadrat hat mehr als eine Wurzel, keine Wurzel mehr als ein Quadrat.
Simpl. Vollkommen richtig.
Salv. Wenn ich nun aber frage, wieviel Wurzeln giebt es, so kann man nicht leugnen, dass sie eben so zahlreich seien, wie die
gesammte Zahlenreihe, denn es giebt keine Zahl, die nicht Wurzel eines Quadrates wäre. Steht dieses fest, so muss man sagen, dass es ebensoviele
Quadrate als Wurzeln gäbe, da sie an Zahl ebenso gross als ihre Wurzeln sind, und alle Zahlen sind Wurzeln; und doch sagten wir anfangs, alle Zahlen
seien mehr als alle Quadrate, da der grössere Theil derselben Nichtquadrate sind. Und wirklich nimmt die Zahl der Quadrate immer mehr ab, je grösser die
Zahlen werden; denn bis 100 giebt es 10 Quadrate, d.h. der 10. Theil ist quadratisch; bis 10000 ist der 100. Theil bloss quadratisch, bis 1000000 nur
der 1000. Theil; und bis zu einer unendlich grossen Zahl, wenn wir sie erfassen könnten, müssten wir sagen, giebt es soviel Quadrate, wie alle
Zahlen zusammen.
Sagr. Was ist denn zu thun, um einen Abschluss zu gewinnen?
Salv. Ich sehe keinen andern Ausweg als zu sagen, unendlich ist die Anzahl aller Zahlen, unendlich die der Quadrate, unendlich
die der Wurzeln; weder ist die Menge der Quadrate kleiner als die der Zahlen, noch ist die Menge der letzteren grösser; und schliesslich haben die
Attribute des Gleichen, des Grösseren und des Kleineren nicht statt bei Unendlichem, sondern sie gelten nur bei endlichen Grössen.
Zermelo-Fraenkel’sches Axiomensystem
![]()
Ernst Zermelo (1871−1953) hat 1907 mit seinen Untersuchungen über die Grundlagen der Mengenlehre eine axiomatisch begründete Theorie entwickelt, und zwar in der Weise, dass „man die Prinzipien einmal eng genug einschränkt, um alle Widersprüche auszuschließen, gleichzeitig aber auch weit genug ausdehnt, um alles Wertvolle dieser Lehre beizubehalten.“ (Math. Annalen Bd. 65, S. 261). Spätere Ergänzungen von Zermelos Prinzipien durch Abraham Halevi Fraenkel (1891−1965) und Albert Thoralf Skolem (1887−1963) führten schließlich zum Zermelo-Fraenkel’schen Axiomensystem mit Auswahlaxiom (Axiom of Choice), in der mathematischen Literatur abgekürzt mit ZFC.
Fraenkel schreibt zum axiomatischen Aufbau der Mengenlehre (Einleitung in die Mengenlehre, 3. Auflage, S.270):
Die Axiome sind Aussagen, die entweder gewisse Relationen zwischen
einer „Menge“ und den „in ihr enthaltenen Elementen“ ausdrücken oder die
Existenz bestimmter Mengen fordern oder endlich gestatten, aus der
Existenz gewisser Mengen allgemein auf die Existenz gewisser anderer
Mengen zu schließen. Danach dürfen der Grundrelation „m ist Element
der Menge M“ keine anderen Eigenschaften zugeschrieben werden als
die, die in den Axiomen ausgedrückt sind oder sich aus den Axiomen
deduktiv ergeben. Ebenso ist unter „Menge“ nicht etwa „jede
Zusammenfassung von Elementen“ zu verstehen, sondern es gibt nur Mengen,
die auf Grund der
Axiome existieren oder herleitbar sind. Schließlich
wird das Wort „Element“ überhaupt nicht zur Bezeichnung eines
selbständigen Begriffs (etwa der „Menge“ gegenüberstehend) gebraucht,
sondern nur als Bestandteil der Grundrelation „Element (einer
Menge) sein“; in der Axiomatik tritt also nur eine einzige Kategorie von
„Dingen“ oder „Objekten“ auf, nämlich die „Mengen“, womit von vornherein
keine bestimmtere Vorstellung als mit dem allgemeinen Ausdruck „Ding“
verbunden zu werden braucht.
In ZFC sind Elemente von Mengen immer ebenfalls Mengen. Das heißt mit anderen Worten: Es existieren in ZFC keine Urelemente (das sind Dinge, die keine Mengen sind, aber Elemente von Mengen sein können). Auf die Frage, was Mengen „eigentlich“ sind, liefert ZFC keine Antwort. Mit ZFC ist es lediglich möglich, Aussagen darüber zu formulieren, dass gewisse mathematische Objekte Mengen sind und welche mengentheoretische Eigenschaften sie haben. Das hört sich sehr schwach an, und dennoch stellt ZFC insbesondere die Basis dafür dar, sowohl die fundamentalen Begriffe der Mathematik mengentheoretisch zu definieren und zu verstehen als auch Grundlagenfragen der Mathematik im Rahmen der Mengenlehre zu diskutieren.
Skolem begann 1929, die Mengenlehre unter Benutzung der Prädikatenlogik zu formalisieren. Alle Aussagen in ZFC können demnach in einer Sprache formuliert werden, deren Zeichen das jeweils Folgende bedeuten soll:
| kleine Buchstaben | Variablen zur Bezeichnung von Mengen |
das Zeichen „=“ |
ist gleich |
| das Zeichen „∈∈“ | ist Element von |
| das Zeichen „˄“ | Junktor und |
| das Zeichen „˅“ | Junktor oder |
das Zeichen „⇀“ |
Junktor wenn, so |
das Zeichen „⇌“ |
Junktor genau dann, wenn |
| das Zeichen „¬“ | Junktor nicht |
das Zeichen „∃“ |
Quantor Es existiert |
das Zeichen „∀“ |
Quantor Für alle |
| das Zeichen „(“ | öffnende Klammer |
| das Zeichen „)“ | schließende Klammer |
| das Zeichen „,“ | Trennzeichen |
Sinnvolle, aus diesen Zeichen gebildete Ausdrücke heißen (zulässige) mengentheoretische Formeln (kurz: Formeln).
Ist eine Variable in einer Formel mindestens einmal weder durch den
Existenzquantor „∃“ noch durch den Allquantor
„∀“ gebunden, so heißt eine solche Variable
freie
Variable. Formeln, in denen keine Variable frei vorkommt, heißen mengentheoretische Aussagen (kurz: Aussagen).
Der Ausdruck "∀a∃b(¬c)"
ist offensichtlich nicht sinnvoll. In der Formel "∃a (a ∈∈ m)"
ist a gebunden und m frei. "∃a ∀m(a ∈∈ m)"
ist eine Aussage, die allerdings falsch ist: Es ist nicht so, dass es eine
Menge a gibt, die Element von jeder Menge ist.
"∀a,b,c (a = b
˄ b = c ⇀ a = c)"
ist eine wahre Aussage und beschreibt die Transitivität bezüglich der Mengengleichheit. Die Aussage lautet ausführlich geschrieben:
∀a∀b∀c (((a = b) ˄ (b = c)) ⇀ (a = c))
Auf die Klammern in Formeln kann man weitgehend verzichten, wenn
vereinbart wird, dass die Bindung der Zeichen „=“
und „∈∈“ am stärksten und die der Zeichen „⇀“
und „⇌“ am schwächsten sein soll. Außerdem soll statt "¬(a = b)"
in der Regel "a ǂ b", statt
"¬(a ∈∈ b)"
"a ∉∉ b"
und statt "¬(∃a)" "∄a"geschrieben werden.
"(x ∈∈ a) ˄ (y ∈∈ a)" wird
abgekürzt durch "x,y ∈∈ a".
Kann die Eigenschaft gewisser Mengen durch eine mengentheoretische Formel beschrieben werden, so heißt diese Eigenschaft
definit und die zugehörige Formel ist ein Prädikat.
Der Ausdruck "∃!m (φ(m))" beispielsweise bedeutet
"Es existiert genau eine Menge m, für die das Prädikat
φ(m)
zutrifft". Er ist logisch äquivalent mit "∃m (∀a (φ(a) ⇌ a = m))"
und nebenbei bemerkt ein Beispiel dafür, dass manchmal - wenn es zweckmäßig
scheint - in Formeln nicht ausschließlich nur die Zeichen verwendet werden,
die oben aufgelistet wurden. Dies ist immer dann erlaubt, solange eine
Formel in eine zulässige Formel überführt werden kann.
Der Ausdruck "∀a (a ∈∈ m ⇀ φ(a))"
bedeutet: "Für alle Mengen a, die Element von m sind, trifft das
Prädikat φ(a) zu". Statt einer Formel der Art "∀a (a ∈∈ m ⇀ φ(a))"
soll auch die folgende kürzere Schreibweise verwendet werden: "∀a∈∈m (φ(a))". Das Prädikat
φT(a,b) =def
∀e (e ∈∈ a ⇀ e ∈∈ b)
beschreibt die Teilmengeneigenschaft der Menge a, genauer:
φT(a,b) drückt aus, dass a eine Teilmenge von b bzw. b
eine Obermenge von a ist (abkürzend geschrieben: a ⊆ b). Mit
φP(a,b) =def
∀e (e ∈∈ b ⇌ φT(e,a))
wird die Potenzmengeneigenschaft der Menge b definiert. Genauer: Durch φP(a,b) wird ausgedrückt, dass b die Potenzmenge von a ist. φT und φP sind zweistellige Prädikate und beschreiben deswegen die Beziehung zwischen zwei Mengen. Im nächsten Beispiel handelt es sich um ein dreistelliges Prädikat:
∀e
((e ∈∈ b ⇀ e ∈∈ a)˄(e ∈∈ a ⇀ e ∈∈ c))
und mit
φN(a) =def
∀e
(e ∉∉ a)
hat man ein einstelliges Prädikat definiert, mit dem ausgedrückt wird, dass die Menge a keine Elemente hat.
Dadurch, dass etwa mit φT(a,b), φP(a,b) oder φN(a,b) bestimmte Mengen formelhaft beschrieben sind, ist nicht ausgesagt, dass derartige Mengen überhaupt existieren!
Mengen, die eine gewisse definite Eigenschaft besitzen, können in einer Klasse zusammengefasst werden. Um Klassen typographisch von Mengen zu unterscheiden, sollen als Klassennamen nur Großbuchstaben zugelassen und statt geschweifter Klammern eckige Klammern verwendet werden:
𝑲 = [ m | φ(m) ].
Der Ausdruck "m ∈∈ 𝑲"
soll "Die Menge m gehört zu 𝑲" bedeuten.
Für "∀x (x ∈∈ m ⇀ x ∈∈ 𝑲)"
soll kurz "m ⊆ 𝑲"
geschrieben werden.
Klassen sind im Allgemeinen keine Mengen. Es wurde im letzten Abschnitt
bereits auf logischem Wege gezeigt, dass beispielsweise die Russell-Zermelo-Klasse 𝑹 = [ m | m ∉∉ m ]
keine Menge ist; im Rahmen von ZFC wird dies später (→ Z3) bewiesen.
In diesem Kapitel werden außer der Allklasse 𝑩 = [ m | m = m ]
noch andere Klassen eine Rolle spielen: etwa die Klasse aller Funktionen 𝑭
oder die Klasse aller Ordinalzahlen 𝑶.
Es sollen nun die Axiome von ZFC nacheinander vorgestellt werden:
Existenzaxiom (EXZ),
Extensionalitätsaxiom (EXT),
Paarmengenaxion (PMG),
Aussonderungsaxiom (AUS),
Potenzmengenaxiom (POT),
Vereinigungsaxiom (VER),
Auswahlaxiom (AWL),
Unendlichkeitsaxiom (INF),
Ersetzungsaxiom (ERS),
Fundierungsaxiom (FND),
Zermelo hat ursprünglich statt EXT und PMG das Axiom der Elementarmengen angegeben, welches insbesondere die Existenz der leeren Menge (von Zermelo Nullmenge genannt) postuliert. In der folgenden Darstellung von ZFC wird stattdessen die Existenz der leeren Menge mit Hilfe von AUS bewiesen. Die Axiome ERS und FND sind dem ursprünglichen Axiomensystem von Zermelo erst später hinzugefügt worden.
Eine Mengenlehre ohne Mengen wäre sinnlos, deswegen lautet das erste Axiom:
Gilt ∀e
(e ∈∈ a ⇀ e ∈∈ b)
für zwei Mengen a und b, so ist a eine Teilmenge
von b, kurz geschrieben: „a ⊆ b“.
Die Aussage
"∀a,b (a = b ⇀ a ⊆ b ˄ b ⊆ a)"
ist demnach offensichtlich wahr. Die Umkehrung dieser Aussage ist nicht selbstverständlich und muss daher axiomatisch festgelegt werden:
![]() Extensionalitätsaxiom (EXT)
Extensionalitätsaxiom (EXT)
Ist a eine Teilmenge von b und b eine Teilmenge
von a, so sind a und b einander gleich.
∀a,b (∀e
(e ∈∈ a ⇌ e ∈∈ b) ⇀ a = b)
Zwei Mengen sind nach dieser Festlegung also immer genau dann gleich, wenn sie in der Gesamtheit aller ihrer Elemente (das heißt, ihrem Umfang nach) übereinstimmen; die Bedeutung oder eine eventuelle Interpretation der Elemente von a bzw. b spielen keine Rolle (extensionale Mengenauffassung).
Wegen ∀e
(e ∈∈ a ⇌ e ∈∈ b) ⇌ a = b
für alle Mengen a, b könnte man im Prinzip die
Gleichheitsbeziehung zwischen zwei Mengen auf die Elementbeziehung
zurückführen und so auf das Zeichen „=“ ganz verzichten.
Gemäß EXT ist jedes Element einer Menge m in m nur einmal enthalten.
![]() Paarmengenaxiom (PMG)
Paarmengenaxiom (PMG)
Seien a und b irgendwelche Mengen. Dann gibt es eine Menge, die genau a und b als Elemente enthält.
∀a,b ∃c ∀d (d ∈∈ c ⇌ (d = a
˅
d = b))
Aus EXT folgt, dass die nach PMG existierende Paarmenge { a, b } eindeutig bestimmt ist. Die Reihenfolge, in der die Elemente einer Paarmenge notiert werden, ist bedeutungslos.
Das Paarmengenaxiom gestattet es, den Begriff „geordnetes Paar“ mengentheoretisch zu definieren, und zwar so, wie es Kazimierz Kuratowski (1896−1980) 1921 vorgeschlagen hat:
Seien x und y zwei beliebige Mengen, dann heißt
(x; y) =def
{ { x }, { x, y } }
geordnetes Paar von x und y.
![]() Z1
Z1
(x; y) ist nach PMG eine Menge und es gilt
(x = u) ˄ (y = v) ⇌ (x; y) = (u; v).
Beweis:
„⇀“: unmittelbar klar.
„↽“: Sei (x; y) = (u; v),
dann gilt
{ { x }, { x, y } } = { { u }, { u, v } }.
Entweder es ist x = y oder es ist x ǂ y.
Im ersten Fall hat man wegen { { x }, { x, x } } = { { x } }
{ { x } } = { { u }, { u, v } }.
Hieraus folgt sowohl u = v als auch
u = x und
wegen x = y auch y = v.
Sei nun der zweite Fall, also x ǂ y, angenommen.
Dann ergibt sich wegen der Zweielementigkeit von { x, y }
{ x } = { u } und { x, y } = { u, v }.
Mit EXT folgt x = u und damit auch
y = v.
"(x; y) = (y; x)"
ist also dann und nur dann
gültig, wenn x = y.
![]() Aussonderungsaxiom (AUS)
Aussonderungsaxiom (AUS)
Sei m eine Menge und φ(e) ein Prädikat. Dann gibt es eine Menge, die genau diejenigen Elemente e von m
enthält, für die φ(e) wahr ist.
∀m ∃x ∀e (e ∈∈ x ⇌ (e ∈∈ m
˄ φ(e)))
φ(e) kann außer e noch weitere freie Variablen enthalten, die man Parameter nennt.
Da es unendlich viele Möglichkeiten gibt, ein Prädikat φ(e) zu formulieren, hat man mit AUS unendlich viele Axiome. AUS nennt man deshalb ein Axiomenschema. Aus EXT folgt, dass die nach AUS zum jeweiligen Prädikat φ(e) existierende Menge x eindeutig bestimmt ist. Man schreibt in der Regel
x = { e ∈∈ m | φ(e) }.
Hierbei ist wesentlich, dass für jedes Element e ∈∈ m nachprüfbar ist, ob φ(e) eine wahre Aussage darstellt oder nicht, wobei hierfür nur die Mengenaxiome, hieraus abgeleitete Aussagen oder allgemeingültige logische Gesetze verwendet werden dürfen.
Bildet man per Komprehension die Gesamtheit von Dingen, die alle eine gemeinsame Eigenschaft haben, so erhält man eine Klasse. Im vorangegangenen Abschnitt wurde bereits deutlich, dass die Klasse aller Mengen
𝑩 = [ m | m = m ],
die so genannte Allklasse, keine Menge ist. Die Allklasse ist also eine echte Klasse. Diese Aussage lässt sich mit Hilfe des Aussonderungsaxioms beweisen, und zwar unter Benutzung des folgenden Satzes:
![]() Z2
Z2
Jede Menge m besitzt mindestens eine Teilmenge, welche nicht
Element von m ist.
Beweis:
Sei m eine beliebige Menge, dann existiert gemäß AUS die eindeutig bestimmte Menge m* mit
m* =def { e ∈∈ m | e ∉∉ e }.
Dann gilt entweder m* ∈∈ m*
oder m* ∉∉ m*.
Unter der Annahme, dass m* ∈∈ m*
wahr ist, würde m* ein Element e mit e ∈∈ e
enthalten (nämlich sich selbst). Allerdings besteht m* nach
Definition aus all den Mengen, die sich nicht selbst enthalten.
Widerspruch zur Annahme! Also folgt m* ∉∉ m*.
Angenommen nun, es wäre m* ∈∈ m,
dann würde aufgrund der Definition von m* auch m* ∈∈ m*
gelten. Widerspruch! Es gilt also m* ∉∉ m.
![]() Z3
Z3
Die Allklasse ist keine Menge.
Beweis:
Wäre die Allklasse 𝑩 eine Menge, dann wäre 𝑩* ∉∉ 𝑩 gemäß des
Beweises von Z2.
Dies ergibt einen Widerspruch, denn 𝑩 umfasst ja nach Definition
alle Mengen, darunter also auch 𝑩*!
Mit dem Aussonderungsaxiom ist sichergestellt, dass neue Mengen nur im Rahmen einer bereits existierenden Menge gebildet werden können.
Erstes Beispiel. Sei m eine Menge und a ⊆ m. Dann heißt
a =def { e ∈∈ m | e ∉∉ a }
Komplementärmenge von a bezüglich m (oder kurz: Komplement von a).
Zweites Beispiel. Seien a und b beliebige Mengen, dann kann man durch
a ∩ b =def { e ∈∈ b
| e ∈∈ a }
den Durchschnitt von a und b definieren.
Sowohl Komplementärmengen als auch Durchschnittsmengen sind aufgrund von AUS Mengen. Eine weitere wichtige Folgerung des Aussonderungsaxioms ist der folgende Satz:
![]() Z4
Z4
Es gibt eine (eindeutig bestimmte) Menge ohne Elemente:
∃!x ∄e (e ∈∈ x).
Beweis:
Sei m eine beliebig gewählte Menge und φE(e,m) =def e ∉∉ m. Dann folgt mit AUS:
∃x ∀e (e ∈∈ x ⇌ (e ∈∈ m
˄
e ∉∉ m)).
Unabhängig von der Wahl von e bzw. m ist die
Aussage "e ∈∈ m
˄
e ∉∉ m" immer falsch.
Also hat man: ∃x ∀e (e ∉∉ x).
Mit EXT folgt: ∃!x ∀e (e ∉∉ x),
was äquivalent ist zur behaupteten Aussage.
Die hiernach eindeutig existierende Menge x heißt leere Menge und wird mit „Ø“ bezeichnet.
![]() Potenzmengenaxiom (POT)
Potenzmengenaxiom (POT)
Zu jeder Menge m gibt es eine Menge, die alle Teilmengen von m enthält.
∀m
∃pm
∀e (e ⊆ m ⇀ e ∈∈ pm)
Gemäß AUS lässt sich dann aus pm eine (nach EXT eindeutige) Menge bilden, die nur die Teilmengen von m enthält:
℘(m) =def
{ e ∈∈ pm | e
⊆
m }.
℘(m) heißt Potenzmenge von
m. Da Ø keine Elemente hat, gilt Ø ⊆ m
bzw. Ø ∈∈ ℘(m)
für jede Menge m.
Zu jeder Menge m gibt es genau eine
Potenzmenge ℘(m). Deshalb kann man
den Ausdruck „℘(m)“ auf zweierlei Art
interpretieren: einerseits kann „℘(m)“
als Bezeichnung der Menge
{ e ∈∈ pm | e ⊆ m }
gesehen werden, andererseits kann man „℘“
als Operator betrachten und „℘(m)“
als Bild unter der Potenzmengenoperation, die eine existierende Menge m
auf ihre Potenzmenge abbildet.
Sei φ(x,y) ein zweistelliges Prädikat und es gelte
∀x
∃!y (φ(x,y))
dann heißt φ(x,y)
rechtseindeutig oder auch funktional. Ein funktionales Prädikat
φ(x,y)
besagt, dass jeder Menge x die eindeutig bestimmte Menge y zugeordnet wird.
Man schreibt hierfür y = F(x). F heißt
(einstelliger) Operator.
Ein funktionales Prädikat φ(x,y) kann unter Umständen außer x und y noch weitere freie Variablen (sogenannte Parameter) enthalten.
Neben einstelligen Operatoren können natürlicherweise auch mehrstellige Operatoren definiert werden:
y = F(x1, x2, x3, ...)
Beispielsweise sieht das Potenzmengenprädikat φP(a,b) - ausführlich geschrieben - so aus:
∀e
(e ∈∈ b ⇌ (∀x
(x ∈∈ e ⇀ x ∈∈ a)))
![]() Z5
Z5
Seien a und b zwei beliebige Mengen, dann gilt
x ∈∈ a ˄ y ∈∈ b ⇀
(x; y) ∈∈ ℘(℘(a ∪ b)).
Beweis:
Aus x ∈∈ a ˄ y ∈∈ b folgt { x }, { x, y } ⊆ a ∪ b,
das heißt: { x }, { x, y } ∈∈ ℘(a ∪ b),
also:
{ { x }, { x, y } } ∈∈ ℘(℘(a ∪ b)),
was zu zeigen war.
Mit φL(g,u) =def
∃v
(g = (u; v)) und
φR(g,v) =def ∃u (g = (u; v)) werden zwei funktionale Prädikate definiert.
φL(g,u) trifft zu, wenn es sich bei g um ein geordnetes Paar und bei u um die linke
Komponente von g handelt; φR(g,v)
trifft zu, wenn es sich bei g um ein geordnetes Paar und bei v
um die rechte Komponente von g handelt. Mit φL
und φR lassen sich die Projektionsoperationen λ
und
ρ und danach das kartesische
Produkt zweier Mengen a und b definieren:
λ(g) =def u,
falls φL(g,u) zutrifft; Ø sonst
ρ(g) =def v,
falls φR(g,v) zutrifft; Ø sonst
Seien a und b zwei beliebige Mengen, sowie p = ℘(℘(a ∪ b)), dann heißt die nach AUS existierende Menge
a x b =def
{ g ∈∈ p | λ(g) ∈∈ a ˄ ρ(g) ∈∈ b }
das kartesische Produkt von a und b.
Wegen Z5 lässt sich a x b auf einfache (und gewohnte) Weise darstellen:
a x b = { (x; y) | x ∈∈ a ˄ y ∈∈ b }.
![]() Z6
Z6
Es gibt ein-elementige Mengen. Präziser: zu jeder
Menge m existiert die Einermenge { m }, das heißt diejenige Menge, die nur m als einziges Element enthält. Bei gegebenem m ist
{ m } eindeutig bestimmt.
Beweis:
Zu jeder Menge m gibt es gemäß POT und EXT die eindeutig bestimmte
Potenzmenge ℘(m). Wegen m ⊆ m
folgt mit AUS die Existenz der Menge
{ t ∈ ℘(m)
| t = { m } } = { m }.
![]() Vereinigungsaxiom (VER)
Vereinigungsaxiom (VER)
Zu jeder Menge m gibt es eine Menge, die alle Elemente der Elemente von m enthält.
∀m ∃vm ∀a,e (a∈∈m
˄ e∈∈a ⇀ e∈∈vm)
Gemäß AUS lässt sich dann aus vm eine (nach EXT eindeutige) Menge bilden, die alle Elemente der Elemente von m umfasst und nur diese:
⋃m =def { e ∈∈ vm
| ∃a (a
∈ m ˄ e ∈∈ a) }
⋃m heißt Vereinigungsmenge von m.
Sei nun t eine nichtleere Menge. Dann gibt es nach AUS zu jedem a ∈∈ ⋃t eine bestimmte Teilmenge ta ⊆ t, zu der all die Elemente von t gehören, die a als Element besitzen:
ta =def
{ e ∈∈ t | a ∈∈ ⋃t
˄ a ∈∈ e
}.
Für jedes a gilt entweder ta = t
oder ta ǂ t. Sei nun
e* ∈∈ t beliebig
gewählt. Dann ist d = { a ∈∈ e* | ta = t }
diejenige Teilmenge von e*, welche alle Objekte enthält, die
Element von jedem Element von t sind.
d heißt Durchschnittsmenge von t und wird mit
∩t bezeichnet.
Enthält t nur zwei Elemente, dann schreibt man
∩{ a, b } = a ∩ b
wie oben bereits definiert.
Seien a und b zwei beliebige Mengen. Dann gibt es gemäß PMG und EXT die eindeutig bestimmte Paarmenge { a, b } und nach VER und AUS die Menge, die alle Elemente von a und b enthält, und nur diese:
⋃{ a, b } = { e ∈∈ v{a,b}
| e ∈∈ a ˅ e ∈ b }.
⋃{ a, b } heißt
Vereinigung von a und b und man schreibt
⋃{ a, b } = a ∪ b.
Die Symbole „∩“ und „∪“
lassen sich als Mengenoperatoren auffassen, mit denen Mengen sinnvoll nur dann
verknüpft werden können, wenn sie Elemente der Potenzmenge einer
beliebig, aber fest gewählten Menge m sind. Die Rechenregeln
bezüglich „∩“ und „∪“
wurden oben bereits behandelt und zeigen, dass „∪“
eine additive und „∩“ eine multiplikative Verknüpfung ist.
Aus dem Vereinigungsaxiom folgt, dass 𝑩’,
die Klasse aller Einermengen, keine Menge ist, denn wäre 𝑩’
eine Menge, würde mit VER folgen, dass auch
𝑩 = ⋃𝑩’
eine Menge ist. Widerspruch, denn 𝑩
ist, wie oben gezeigt wurde, eine echte Klasse. Entsprechend folgt
auch, dass 𝑩’’,
die Klasse aller Zweiermengen, keine Menge ist, und so fort.
![]() Auswahlaxiom
(AWL)
Auswahlaxiom
(AWL)
Ist m eine Menge von paarweise disjunkten und nichtleeren Mengen, dann gibt es eine Menge, die genau ein Element aus jedem Element
von m enthält. Für jede Menge m mit
∀x,y∈∈m (x,y ǂ Ø ˄ (x = y ˅ x∩y = Ø))
folgt also
∃a ∀x∈∈m (∃z (a∩x = { z })).
Seien m und a Mengen wie in AWL beschrieben, dann besteht a*, definiert durch a* =def a ∩ ⋃m, nur aus den „ausgewählten“ Elementen z. a* heißt Auswahlmenge für m.
Das Auswahlaxiom postuliert zwar die Existenz von Auswahlmengen, bietet aber grundsätzlich keinerlei Möglichkeit, einen Weg anzugeben, wie man diese Mengen bilden könnte. Von daher ist es nicht verwunderlich, dass viele Mathematiker dem nicht-konstruktiven Auswahlaxiom kritisch bis ablehnend gegenüber standen. Andererseits wird das Auswahlaxiom für den Beweis wichtiger mathematischer Gesetzmäßigkeiten gebraucht; es wird zum Beispiel benötigt, um den Wohlordnungssatz zu beweisen.
Zermelo hat die Notwendigkeit des Auswahlaxioms damit
begründet, dass das Produkt mehrerer Mengen nur dann verschwinden
(das heißt, der leeren Menge gleich sein) soll, wenn einer der Faktoren
verschwindet (Math. Annalen Bd. 65, S. 266). Er geht bei der
Einführung des Produktes von einer Menge t aus, deren Elemente
paarweise disjunkt sind. Dann definiert er 𝔓t
als Menge, die all diejenigen Teilmengen der Vereinigungsmenge von t umfasst, welche mit jedem Element von t genau ein Element gemeinsam
haben und nennt diese Menge die zu t gehörende Verbindungsmenge (oder:
das Produkt der Elemente von t). 𝔓t ist nach VER, AUS
sowie Z6 eine wohldefinierte Menge:
𝔓t =def { u ⊆ ⋃t | ∀m∈∈t ∃z (u ∩ m = { z }) }.
Mit dem Auswahlaxiom folgt nunmehr wie gefordert:
𝔓t = Ø ⇌ Ø ∈∈ t.
Zermelo schreibt weiter: „Die vorstehenden Axiome genügen, wie wir sehen werden, um alle wesentlichen Theoreme der allgemeinen Mengenlehre abzuleiten. Um aber die Existenz ‚unendlicher Mengen‛ zu sichern, bedürfen wir noch des folgenden, seinem wesentlichen Inhalte von Herrn Dedekind herrührenden Axiomes.“ Das ursprüngliche Axiom der Unendlichkeit postuliert die Existenz einer Menge, die Ø als Element enthält und mit jedem Element e dieser Menge auch { e } als Element enthält. Dies führt dann zur von Zermelo so genannten Zahlenreihe Ø, { Ø }, { { Ø } }, ...
Das Unendlichkeitsaxiom in der hier angegebenen Fassung basiert auf einem Vorschlag von John von Neumann (1903−1957):
![]() Unendlichkeitsaxiom (INF)
Unendlichkeitsaxiom (INF)
Es existiert eine Menge, die Ø als Element enthält und mit jedem Element
e dieser Menge auch e ∪ { e } als Element enthält.
∃m (Ø∈∈m ˄ ∀e (e∈∈m ⇀ e ∪ { e } ∈∈ m))
Eine nach INF existierende Menge m nennt man eine induktive Menge.
Alle induktiven Mengen haben eine gemeinsame Teilmenge. (→ Beweis, gemäß der Argumentation von Zermelo 1907 und unter Benutzung seiner Symbole). Diese Teilmenge, ab jetzt mit ω bezeichnet, besteht aus dem Element Ø und aus denjenigen Elementen, die - ausgehend von Ø - induktiv erzeugt werden:
Ø
{ Ø }
{ Ø, { Ø } }
{ Ø, { Ø }, { Ø, { Ø } } }
...
Abraham Fraenkel wies 1922 in seinem Aufsatz Zu den Grundlagen der Cantor-Zermeloschen Mengenlehre (Mathematische Annalen 86, S. 230−237) darauf hin, dass die Axiome von Zermelo nicht zur Begründung der Mengenlehre ausreichen und gab als Nachweis dieser Aussage unter anderem ein einfaches Beispiel: Es sei Z0 die Zermelo’sche Zahlenreihe, Z1 die Potenzmenge von Z0, Z2 die Potenzmenge von Z1, und so fort. Dann lässt sich auf der Grundlage der bisherigen Axiomen nicht die Menge { Z0, Z1, ... } und daher auch nicht die Vereinigungsmenge dieser Menge bilden.
Fraenkel schlug damals vor, Zermelos Axiomensystem durch das von ihm so
genannte Ersetzungsaxiom zu ergänzen: „Ist M eine Menge und
wird jedes Element von M durch ein ‚Ding des Bereiches ℬ‛
... ersetzt, so geht M wiederum in eine Menge über.“ und er
kommentiert dies (auf S. 231) so:
Für das oben angeführte Beispiel hat man, um die
Existenz der Menge { Z0, Z1, ... }
zu zeigen, auf Grund des soeben formulierten Axioms nur das Element 0 von Z0
durch Z0, das Element { 0 } durch Z1 zu
ersetzen usw. Man kann weiter auf die Vereinigungsmenge der so entstehenden
Menge das Axiom in analoger Weise anwenden und erlangt, derart
weiterschreitend, ersichtlich die erforderliche Freiheit in der Bildung von
Mengen.
Für die speziellen Zwecke der Axiomatik der Mengenlehre ist es übrigens ...
wünschenswert und möglich, an Stelle des angeführten Axioms ein weniger
weitgehendes und schärferes aufzustellen; es gelingt dabei, den Begriff
„ersetzen“, der im wesentlichen auf den Funktionsbegriff hinausläuft und
einer besonderen Einführung bedürfte, überflüssig zu machen.
Heute wird das Ersetzungsaxiom etwa wie folgt formuliert:
![]() Ersetzungsaxiom (ERS)
Ersetzungsaxiom (ERS)
Sei φ(x,y) ein funktionales Prädikat. Ersetzt man jedes Element x einer Menge durch das durch
φ(x,y)
eindeutig gegebene y, erhält man wieder eine Menge.
Präziser: Mit φxy =def φ(x,y) gilt
∀φxy(∀x,y,z (φxy ˄ φxz ⇀ y = z) ⇀
∀v ∃w ∀x,y (x ∈∈ v ˄ φxy ⇀ y ∈∈ w))
ERS ist genauso wie AUS ein Axiomenschema für unendlich viele Axiome.
Ist v eine Menge, φxy funktional und F der zu φxy gehörende Operator, dann folgt wegen ERS und AUS, dass
F(v) =def { y | ∃x(x ∈∈ v ˄ φxy) }
eine Menge ist. F(v) ist nach EXT eindeutig bestimmt und heißt Bild von v unter dem Prädikat φxy.
Fraenkel bemerkt in seinem eben zitierten Aufsatz (auf S. 234), dass das Axiomensystem von Zermelo nebst seiner Ergänzung durch das Ersetzungsaxiom, „die Gesamtheit der Mengen nicht vollständig festlegt“. Im Übrigen beklagt er zwei weitere „Übelstände“: 1. Zwar sind Mengen „nichtmathematischer und überhaupt nichtbegrifflicher Herkunft“ mithilfe der Axiome nicht konstruierbar, allerdings wird die Existenz solcher Mengen durch die Axiome nicht ausgeschlossen. 2. Zermelos Axiome lassen es zu, dass es Mengen mit unerfreulichen Eigenschaften gibt, zum Beispiel zyklische Mengen m, deren Elemente alle die Eigenschaft haben, Element des „nächsten“ Elementes von m zu sein: e1 ∈∈ e2 ∈∈ e3 ... ∈∈ en ∈∈ e1.
Den angegebenen Übelständen kann nach Fraenkel durch ein „... ‚Beschränktheitsaxiom‛ abgeholfen
werden, das dem Mengenbegriff oder zweckmäßiger dem Bereich ℬ
den geringsten mit den übrigen Axiomen verträglichen Umfang
auferlegt“.
Diese Idee von Fraenkel wird realisiert durch das Fundierungsaxiom, welches tatsächlich die charakteristische Struktur des gesamten Mengenuniversums bestimmt (→ vonNeumann’sche Hierarchie) .
![]() Fundierungsaxiom (FND)
Fundierungsaxiom (FND)
Jede nichtleere Menge m enthält ein Element e, so dass
e und m disjunkt sind, mit anderen Worten: jede nichtleere
Menge ist fundiert.
∀m
(m ǂ Ø ⇀ ∃e (e ∈∈ m
˄ e ∩ m =
Ø))
In jeder nichtleeren Menge m gibt es also mindestens ein Element, das kein Element mit m gemeinsam hat; man nennt ein solches Element ∈∈-minimales Element.
Angenommen, es gäbe eine zyklische Menge m. Sei e** ∈∈ m beliebig gewählt, dann gibt es immer ein e* ∈∈ m mit e* ∈∈ e** und e* ∈∈ (e** ∩ m), das heißt (e** ∩ m) ǂ Ø. So kann man für alle e** ∈∈ m bzw. für alle e* ∈∈ m in beliebiger Reihenfolge argumentieren. Das bedeutet: Aufgrund von FND kann es keine zyklischen Mengen geben.
Es gibt auch keine Mengen, die Element von sich selbst sind: Angenommen, es gäbe eine solche Menge m mit m ∈∈ m. Mit m existiert auch { m } und es gilt m ∈∈ (m ∩ { m }). Widerspruch zu FND!
Die Existenz zweier Mengen a und b mit a ∈∈ b ˄ b ∈∈ a ist ebenfalls ausgeschlossen. Denn gäbe es solche Mengen, würde die gemäß PMG existierende Menge { a, b } zyklisch sein. Widerspruch zu FND!
Seien a und b zwei beliebige Mengen und φ(x,y) ein Prädikat. Dann ist die gemäß AUS existierende Menge
r = { (x; y) ∈∈ a x
b | φ(x,y) }
eine Relation zwischen a und b. Ist r ⊆ a x a, dann wird r eine Relation auf a
(manchmal auch Relation in oder über a) genannt.
Statt „(x; y) ∈∈ r“
wird üblicherweise auch „x r y“ geschrieben.
Ersetzt man gemäß ERS jedes Element (x; y) von r durch die linke Komponente von (x; y), erhält man die nach EXT eindeutig bestimmte Menge
dom(r) =def
{ λ(g) | g ∈∈ r } =
{ x | ∃y ((x; y) ∈∈ r) },
den so genannten Definitionsbereich von r (englisch: domain). Die Menge
rng(r) =def
{ ρ(g) | g ∈∈ r } =
{ y | ∃x ((x; y) ∈∈ r) }
heißt Wertebereich von r (englisch: range).
fld(r) =def ⋃⋃r
heißt Feld von r (englisch: field).
Mit der Definition eines geordneten Paares folgt unmittelbar
r ⊆ a x a mit a = fld(r).
Außerdem gilt fld(r) = dom(r) ∪ rng(r). Die Klasse aller Relationen auf einer Menge a, nämlich
℘(a x a), ist gemäß POT eine Menge.
Sei a eine Menge von paarweise disjunkten und nichtleeren Mengen, also eine Zerlegung von ⋃a. Diese Zerlegung induziert eine Äquivalenzrelation auf ⋃a und die Elemente von a sind die zugehörigen Äquivalenzklassen. Das Auswahlaxiom besagt, dass sich zu jeder dieser Äquivalenzklassen immer ein Repräsentant auswählen lässt, wobei keine Aussage darüber möglich ist, wie und auf welchem Weg diese Auswahl zu bewerkstelligen sein könnte.
Ist f eine Relation zwischen a und b und gilt für alle x ∈∈ a und für alle y, y* ∈∈ b
(x; y) ∈∈ f ˄ (x; y*) ∈∈ f ⇀
y = y*,
so nennt man f eine Funktion. Die Klasse aller
Funktionen sei mit „𝑭“ bezeichnet.
Anstatt „f ∈∈ 𝑭 ˄ dom(f) =
a ˄ rng(f) ⊆
b“ soll abkürzend „f: a → b“
geschrieben werden (man sagt: „f ist eine Funktion von a nach b“).
b heißt Zielbereich von f. Ist (x; y) ∈∈ f
bzw. x f y, dann schreibt man (wie gewohnt) „y = f(x)“
und nennt y das Bild von x unter f
und x Urbild von y unter f.
Sei f: a → b. Wenn x ǂ x* ⇒
f(x) ǂ f(x*)
für alle x, x* ∈∈ dom(f)
gilt, dann nennt man f eine Injektion: f: a inj→ b. Gilt f: a → b
und
rng(f) = b, dann nennt man f eine Surjektion und man sagt,
dass f „eine Funktion von a auf b“ ist: f: a sur→ b. Ist f eine Injektion und eine Surjektion, dann heißt f Bijektion: f: a bij→ b.
Aus mengentheoretischer Sicht ist also jede Funktion eine Menge,
präziser: eine Teilmenge des kartesischen Produktes zweier Mengen im
Gegensatz zur Definition einer Funktion als Tripel, bestehend aus
Definitionsbereich, Zielbereich und Zuordnungsvorschrift. Da Ø Teilmenge
von jeder Menge ist, ist auch Ø eine Funktion (die leere Funktion). Es ist
dom(Ø) = Ø, rng(Ø) = Ø und f: Ø → b mit beliebiger Menge b.
Aus f: a → b folgt f ∈∈ ℘(a x
b). Demzufolge ist die Klasse ab aller
Funktionen von a nach b wegen AUS eine Menge:
ab =def
{ f ∈∈ ℘(a x
b) | f: a → b }
Ist f eine Funktion und g ⊆
f, dann ist g auch eine Funktion; anders ausgedrückt: 𝑭, die Klasse
aller Funktionen, ist bezüglich „⊆“ abgeschlossen.
Sei f: a inj→ b. Dann
existiert gemäß ERS die Menge
f−1 =def
{ (y; x) | (x; y) ∈∈ f }.
Wegen der Injektivität von f ist f−1
ebenfalls eine Funktion. dom(f−1) = rng(f). f−1
heißt Umkehrfunktion von f (oder Inverse von f). Die Umkehrfunktion einer Bijektion von a auf b ist eine Bijektion
von b auf a. Gilt f: a bij→ a, so nennt man f eine
Permutation von a. Die Bijektion ida mit ida(x) = x
für alle x ∈∈ a heißt identische Funktion
auf a.
Bijektionen sind insbesondere deswegen wichtig, weil sie es gestatten, Mengen ihrem Umfang nach miteinander zu vergleichen:
Zwei Mengen a und b heißen gleichmächtig (oder äquivalent) genau dann, wenn eine Funktion f existiert, so dass f: a bij→ b. Man schreibt in diesem Fall: „a ∼ b“ und „f: a ∼ b“ (→ Mächtigkeiten).
Sind f und g Funktionen mit rng(f) ⊆ dom(g), dann existiert gemäß AUS die Menge
{ x ∈∈ dom(f) x rng(g) | ρ(x) = g(f(πl(x))) },
einfacher formuliert: { (u; g(f(u))) | u ∈∈ dom(f) }.
Also ist die folgende Definition statthaft:
Seien f und g zwei Funktionen mit rng(f) ⊆ dom(g), dann heißt
g∘=def
{ (u; g(f(u))) | u ∈∈ dom(f) }
Hintereinanderschaltung (oder: Komposition) von f und g.
Sind f und g Funktionen mit dom(g) ⊆ dom(f) und f(x) = g(x)
für alle x ∈∈ dom(g),
dann heißt f eine Fortsetzung von g; umgekehrt ist g eine Restriktion von f.
Sei f eine Funktion und a eine Teilmenge von dom(f). Dann wird die Restriktion von f auf a wie folgt definiert:
f|a =def f
∩ (a x rng(f))
Sei f ∈∈ 𝑭 und a ⊆
dom(f), dann gilt f|a ⊆ f ˄ f|a ∈∈ 𝑭,
dom(f|a) = a
und f|a(x) = f(x)
für alle x ∈∈ a.
Sei m eine nichtleere Menge und f eine Funktion mit dom(f) = m und es gelte
∀x (x
∈∈ m ˄ x ǂ Ø ⇀
f(x) ∈∈ x).
Dann heißt f Auswahlfunktion auf m.
![]() R1
R1
Sei m eine nichtleere Menge. Dann gibt es auf ℘(m)
eine Auswahlfunktion.
Beweis:
Sei m nicht leer und ansonsten beliebig gewählt. Dann existiert
gemäß AUS die Menge
p =def { { u } x u | u ∈∈ ℘(m) },
denn für jede Menge u ist wegen Z6 auch { u } eine Menge und das kartesische Produkt aus u und { u } ist ebenfalls eine Menge.
p besteht nach Definition aus nichtleeren und zueinander disjunkten Mengen. Es existiert also aufgrund des Auswahlaxioms eine Auswahlmenge für p. Nennt man diese Auswahlmenge a, so gilt für jedes Element e von a
e = (u; v)
mit v ∈∈ u
und es gibt nach Definition von p für jedes u ∈∈ ℘(m)
ein derartiges e ∈∈ a. Demnach ist a ∪ { (Ø; Ø) }
eine Auswahlfunktion auf ℘(m), was
zu zeigen war.
![]() R2
R2
Sei m eine nichtleere Menge. Dann gibt es auf m eine Auswahlfunktion.
Beweis:
Sei m nicht leer, aber ansonsten beliebig gewählt.
Dann gibt es nach R1 eine
Auswahlfunktion auf ℘(⋃m),
etwa a.
Wegen m ⊆ ℘(⋃m)
ist a|m eine Auswahlfunktion auf m.
![]() R3
R3
Wenn k eine Funktionenkette ist, so ist ⋃k
eine Funktion und es gilt
dom(⋃k) = ⋃{ dom(f) | f ∈∈ k }.
Beweis:
(i) zu zeigen: ⋃k ∈∈ 𝑭.
⋃k
=∃f (f ∈∈ k ˄ g ∈∈ f) }
= { (x; y) |
∃f (f ∈∈ k
˄ (x ∈∈ dom(f) ˄ y = f(x))) }
= { (x; y) |
∃f ((f ∈∈ k
˄ x ∈∈ dom(f)) ˄ y = f(x)) }
Angenommen, (x; y),(x; y*) ∈∈ k
mit y ǂ y*.
Dann existieren zwei Funktionen f,g
∈ k mit
(x; y) ∈∈ f ˄ (x; y*) ∈∈ g ˄ f ǂ g.
k ist eine Funktionenkette. Also ist entweder f ⊂ g
oder g ⊂ f.
f ⊂ g ⇒ (x; y),(x; y*) ∈∈ g
Widerspruch, weil g ∈∈ 𝑭.
g ⊂ f ⇒ (x; y),(x; y*) ∈∈ f
Widerspruch, weil f ∈∈ 𝑭.
Aus (x; y),(x; y*) ∈∈ k
folgt demnach stets y = y*, also ist
⋃k eine Funktion.
(ii)
dom(⋃k) = { x |
∃f (f ∈∈ k ˄
(x; y) ∈∈ f) }.
Sei df =def dom(f)
und vf =def {dom(f) | f ∈∈ k },
dann ist ⋃v = { x |
∃df (df ∈∈ vf ˄ x ∈∈ df) };
zu zeigen: dom(⋃k) = ⋃v.
Sei x ∈∈ dom(⋃k).
Dann existieren f ∈∈ k
und y ∈∈ ω mit
(x; y) ∈∈ f.
Wegen f ∈∈ k ist
df ∈∈ vf
˄ x ∈∈ df,
also folgt x ∈∈ ⋃v.
Sei umgekehrt x ∈∈ ⋃v.
Dann existiert ein df mit df ∈∈ vf ˄ x ∈∈ df.
Wegen df ∈∈ vf ist (1) f ∈∈ k.
Wegen x ∈∈ df
gibt es ein y mit (2) (x; y) ∈∈ f.
Aus (1) ˄ (2) folgt x ∈∈ dom(⋃k).
Mit EXT folgt dom(⋃k) = ⋃v.
Die eben bewiesene Aussage R3 spielt später im Beweis vom Rekursionssatz für ω eine wichtige Rolle.
Ist m eine nichtleere Menge und f: m → m oder f: m x m → m, so nennt man f eine (einstellige bzw. zweistellige) Verknüpfung (auf m bzw. auf m x m) und (m, f) eine algebraische Struktur. Existiert auch eine Relation r auf m, die für die Struktur von m wichtig ist, so erweitert sich das Tupel (m,f) zu (m,f,r). Gibt es darüberhinaus noch ein Element c von m, dem bezüglich f oder r eine besondere Bedeutung zukommt, erhält man das Quadrupel (m,f,r,c).
Man könnte den Begriff „algebraische Struktur“ allgemeiner fassen; dies wäre aber für dieses Kapitel ohne Belang.
Seien A = (a,f,r,c) und
B = (b,g,s,d) algebraische
Strukturen. Dann ist ψ genau dann ein Isomorphismus von
A auf B (in Zeichen: „ψ: A ≅ B“),
wenn Folgendes gilt:
ψ: a bij→ b
∀x∈∈a (ψ(f(x)) = g(ψ(x))),
falls f,g einstellig
∀x,y∈∈a (ψ(f(x; y)) = g(ψ(x); ψ(y))),
falls f,g zweistellig
∀x,y∈∈a (x r y ⇌ ψ(x) s ψ(y))
ψ(c) = d
Wenn ein Isomorphismus von A auf B
existiert, dann sagt man „A und B sind isomorph“ (in
Zeichen: „A ≅ B“).
![]() R4
R4
Seien A = (a,f,r,c)
und
B = (b,g,s,d)
algebraische Strukturen und ψ: A ≅ B.
Wegen der Injektivität von ψ existiert ψ−1
und es gilt
ψ−1: b bij→ a. Darüberhinaus gilt
ψ−1: B ≅ A.
Beweis:
Seien x*,y* ∈∈ b beliebig gewählt.
Dann gibt es x,y ∈∈ a
mit ψ(x) = x* ˄ ψ(y) = y*.
Falls f und g zweistellige Verknüpfungen sind, gilt ψ(f(x; y)) = g(x*; y*)
wegen ψ: A ≅ B
und damit hat man
ψ−1(x*; y*) = f(x; y) = f(ψ−1(x*); ψ−1(y*)).
Sind f und g einstellige Verknüpfungen, so folgt ψ−1(x*) = f(x) = f(ψ−1(x*))
aus ψ(f(x)) = g(x*).
Seien x*,y* ∈∈ b
nun so gewählt, dass x* s y*.
x* s y*
ψ(x) s ψ(y)
⇌
x r y
⇌
ψ−1(x*) r ψ−1(y*).
⇌
Schließlich gilt noch ψ(c) = d ⇌ ψ−1(d) = c.
Sind zwei Strukturen A und B isomorph, so haben diese also völlig gleiche strukturelle Eigenschaften. Man sagt dann: „A und B sind bis auf Isomorphie gleich“. Gilt ein Satz für Elemente aus a bezüglich f bzw. r, so ist der gleiche Satz für Elemente aus b bezüglich g bzw. s ebenfalls gültig. Das Umgekehrte ist natürlich auch richtig.
Auf Grundlage des Unendlichkeitsaxioms können die natürlichen Zahlen als
Mengen repräsentiert werden; es sind dies Ø, { Ø }, { Ø, { Ø } }, { Ø, { Ø }, { Ø, { Ø } } }, ...,
also die Elemente der Menge ω (vonNeumann’sche Zahlen). Definiert
man 0 =def Ø, 1 =def { Ø },
2 =def { Ø, { Ø } },...,
n, s(n) =def n ∪ { n },
...
unter Benutzung der „gewöhnlichen“ natürlichen Zahlen 0, 1, 2, ..., n, n+1, ... so gilt
für beliebiges n und die Nachfolgermenge n+1
n+1 = { 0, 1, ..., n }.
Diese mengentheoretische Definition und Beschreibung der natürlichen Zahlen ist nur dann sinnvoll, wenn der Nachweis gelingt, dass ω dem Axiomensystem von Peano genügt, wenn man zeigen kann, dass die Elemente von ω linear angeordnet werden können und dass ℕ und ω strukturgleich sind.
Die Peano’schen Axiome lauten unter Benutzung der im vorigen Abschnitt definierten Begriffe und Schreibweisen
(I)* w ǂ Ø
(II)* ∃σ (σ: w inj→ w)
(III)* ∃! o ∈∈ w (o ∉∉ rng(σ))
(IV)* ∀t⊆w (o∈∈t ˄ ∀x∈∈t (σ(x) ∈∈ t) ⇀ t = w)
o heißt Nullmenge, σ wird Nachfolgerfunktion genannt. Sind die Axiome (I)* bis (IV)* gültig, dann sagt man kurz: „(w,σ,o) ist eine Peano-Struktur“.
Es werden nun nacheinander die folgenden Sätze bewiesen:
(ω,s,Ø) ist eine Peano-Struktur
mit s(x) = x ∪ { x }
für alle x ∈∈ ω.
Die Elemente von ω sind transitive Mengen.
Die Elemente von ω lassen sich linear ordnen.
Für alle n ∈∈ ω
ist s(n) das nach n nächstgrößere Element.
Zu jedem n von ω gehören alle Elemente von
ω, die kleiner sind als n.
ω ist wohlgeordnet.
Auf ω können Funktionen rekursiv definiert werden.
Es gilt der spezielle Rekursionssatz für
ω.
Je zwei Peano-Strukturen sind isomorph zueinander.
![]() N1
N1
(ω,s,Ø) ist eine Peano-Struktur
mit s(x) = x ∪ { x }
für alle x ∈∈ ω.
Der Beweis dieses Satzes wird in zwei Teilen geführt:
Beweis (erster Teil):
(i)
(I)* gilt, denn Ø ∈∈ ω.
Sei s =def { e ∈∈ ω x
ω
| πr(e) = πl(e) ∪ { πl(e) } }.
s ist gemäß AUS wohldefiniert und
es gilt
s:ω → ω
mit s(x) = x ∪ { x },
wegen x ∈∈ ω ⇀ x ∪ { x } ∈∈ ω
für alle x ∈∈ ω
(ω eine induktive Menge!),
und s ist rechtseindeutig.
Aus x = y folgt mit EXT { x } = { y }
und somit gilt auch s(x) = s(y).
(iii)
Nach Definition von s gilt für alle y ∈∈ rng(s):
∃x (x ∈∈ ω
˄ y = x ∪ { x }),
woraus folgt, dass y ǂ Ø für alle y ∈∈ rng(s).
Also gilt Ø ∉∉ rng(s),
womit (III)* erfüllt ist mit o = Ø.
(iv)
ω ist die „kleinste“ induktive Menge, präziser:
jede Teilmenge t von ω ist keine induktive Menge,
das heißt für alle t ⊆ ω:
Ø ∈∈ t ˄ ∀x∈∈t (s(x) ∈∈ t) ⇀ t = ω.
Dies ist genau die Aussage von (IV)*,
wenn w = ω.
Im Folgenden soll mit „φn=m“ die Aussage „φn
trifft zu für m“ gemeint sein. „φn∈∈ω“
bedeutet demzufolge „φn
trifft zu für alle n ∈∈ ω“.
Sei nun φn =def φ(n)
ein Prädikat mit der Eigenschaft
φn=Ø ˄ ∀m∈∈ω (m ∈∈ ω ˄ φn=m ⇀ φn=s(m)).
Dann folgt mit t =def { n ∈∈ ω | φn } und (iv)
die Gleichheit von t und ω, und dies
bedeutet, dass φn für alle n ∈∈ ω zutrifft.
Damit ist (unter wesentlicher Verwendung von INF) der Satz von der vollständigen Induktion über ω (kurz: Induktionssatz für ω) bewiesen:
φn=Ø ˄ ∀m∈∈ω (φn=m ⇀ φn=s(m)) ⇀ φn∈∈ω.
φn=Ø heißt Induktionsanfang,
(m ∈∈ ω ˄ φn=m)
Induktionsvoraussetzung und
(m ∈∈ ω ˄ φn=m ⇀ φn=s(m))
Induktionsschluss.
Bevor der oben mit (i), (iii) und (iv) begonnene Beweis fortgeführt wird, soll zuvor erst noch die folgende wichtige Aussage bewiesen werden:
![]() N2
N2
Alle Elemente von ω sind transitive Mengen, das heißt:
TM ∀n,x (n ∈∈ ω ˄ x ∈∈ n
⇀ x ⊆ n)
Beweis:
Sei φn =def ∀x (x ∈∈ n ⇀ x
⊆ n).
zu zeigen: φn∈∈ω,
mit anderen Worten: φn trifft für alle n ∈∈ ω zu.
Induktionsanfang:
Es gilt φn=Ø, denn Ø besitzt kein Element und deshalb gibt es nichts nachzuweisen.
Induktionsvoraussetzung:
Es gelte φn=m für ein beliebig gewähltes m ∈∈ ω.
Induktionsschluss:
Wegen φn=m gilt x
⊆ m
für alle x ∈∈ m.
s(m) = m ∪ { m }.
Sei nun x ∈∈ s(m).
Dann gilt (1) x ∈∈ m
oder (2) x ∈∈ { m }.
(1)
⇒ x ⊆ m nach Induktionsvoraussetzung
⇒ x ⊆ s(m) wegen m
⊆ s(m).
(2)
⇒ x = m
⇒ x ⊆ s(m) wegen EXT
Es gilt also auch φn=s(m) und damit die behauptete Aussage.
Im Beweis von N1 fehlt noch der Nachweis, dass s:ω → ω
mit s(x) = x ∪ { x } eine Injektion ist:
Beweis (zweiter Teil):
(ii)
Sei s(x) = s(y) für
x,y ∈∈ ω angenommen,
dann ist zu zeigen, dass x = y gilt.
Aus s(x) = s(y) folgt zunächst nach Definition von
s
x ∪ { x } = y ∪ { y }.
Damit gilt entweder x = y oder x ∈∈ y ˄ y ∈∈ x.
Aus x ∈∈ y ˄ y ∈∈ x
folgt wegen TM x ⊆ y ˄ y ⊆ x.
Mit EXT folgt x = y und damit (II)*.
Hiermit ist bewiesen, dass (ω,s,Ø) eine Peano-Struktur ist: die Trägermenge ω genügt den Axiomen (I)* bis (IV)*, s ist die Nachfolgerfunktion auf ω und Ø repräsentiert die Nullmenge.
Als Nächstes soll (mit N3 und N4) gezeigt werden, dass die Elemente von ω angeordnet werden können, und zwar mit der ∈∈-Relation auf ω, definiert durch
∈∈ω =def { g ∈∈ ω x ω |
λ(g) ∈∈ ρ(g) }.
"(x; y) ∈∈ ∈∈ω" ist gleichbedeutend mit "x ∈∈ω y"; für "x ∈∈ω y" soll im Folgenden der Einfachheit halber nur "x ∈∈ y" geschrieben werden.
![]() N3
N3
Es gilt für alle x,m ∈∈ ω
m ∈∈ x ⇀ s(m) ∈∈ x ˅ s(m) = x.
Beweis durch vollständige Induktion über x:
Für x = Ø gibt es nichts zu zeigen, denn "m ∈∈ Ø" ist für alle m falsch.
Es gelte m ∈∈ k ⇀ s(m) ∈∈ k ˅ s(m) = k
für ein beliebiges, aber fest gewähltes k ∈∈ ω.
Sei nun m ∈∈
s(k).
⇒ m ∈∈ k ˅ m = k,
⇒ (s(m) ∈∈ k
˅ s(m) =
k) ˅ m = k
(nach Induktionsvoraussetzung)
⇒ (s(m) ∈∈ k ˅ s(m) =
k) ˅ s(m) = s(k) (s ist rechtseindeutig!)
⇒ (s(m) ∈∈ s(k)) ˅ s(m) = s(k) (nach Definition von
s).
![]() N4
N4
ω ist mit „∈∈“ linear geordnet: ∈∈ω
ist irreflexiv, transitiv und konnex:
∄x (x ∈∈ x) (Irreflexivität)
∀x,y,z (x ∈∈ y ˄ y ∈∈ z ⇀ x ∈∈ z) (Transitivität)
∀x,y (x ∈∈ y
˅ x = y ˅ y ∈∈ x) (Konnexität)
Beweis:
Seien im Folgenden x, y und z Elemente von ω.
(i) Als Folgerung aus FND wurde oben bereits notiert, dass es keine
Menge gibt, die sich selbst als Element besitzt. Damit ist die Irreflexivität von ∈∈ω bereits bewiesen.
(ii) Aus x ∈∈ y ˄ y ∈∈ z folgt mit TM x ∈∈ y ˄ y ⊆ z,
also gilt auch x ∈∈ z.
(iii) Sei φn = φ(n) =def
∀x (n ∈∈ x ˅ n = x ˅ x ∈∈ n).
zu zeigen:
φn∈∈ω,
mit anderen Worten: φ(n) trifft für alle n ∈∈ ω zu.
Induktionsanfang:
zu zeigen: φn=Ø, das heißt:
∀x (Ø ∈∈ x ˅ Ø = x ˅ x ∈∈ Ø).
Es genügt zu zeigen, dass ∀x (Ø ∈∈ x ˅ Ø = x),
denn "x ∈∈ Ø" ist für alle x eine falsche Aussage.
"∀x (Ø ∈∈ x
˅ Ø = x)"
wird bewiesen durch vollständige Induktion über x:
"Ø ∈∈ Ø ˅ Ø = Ø" ist eine wahre
Aussage, denn "Ø = Ø" ist wahr.
Es gelte nun Ø ∈∈ m ˅ Ø = m für ein beliebig
gewähltes m ∈∈ ω.
Es folgt sofort Ø ∈∈ s(m) wegen
s(m) = m ∪ { m }.
Induktionsvoraussetzung:
Es gelte φn=m für ein beliebig gewähltes m ∈∈ ω, also:
∀x (m ∈∈ x ˅ m = x ˅ x ∈∈ m).
Induktionsschluss:
zu zeigen: φn=s(m), das bedeutet:
∀x (s(m) ∈∈ x ˅ s(m) = x
˅ x ∈∈ s(m)).
Falls x ∈∈ m, so gilt wegen
s(m) = m ∪ { m }
auch x ∈∈ s(m).
Falls m = x, so gilt x ∈∈ { m } und somit ebenso x ∈∈
s(m).
Im Fall "m ∈∈ x"
folgt nach N3 s(m) ∈∈ x ˅ s(m) = x.
Man macht sich schnell klar, dass von den Aussagen "x ∈∈ y",
"x = y" und
"y ∈∈ x" für zwei beliebig
ausgewählte x, y ∈∈ ω
stets nur genau eine Aussage richtig sein kann: Sowohl "x ∈∈ y ˄ x = y" als
auch "y ∈∈ x ˄ x = y" können
nie gelten, da ∈∈ω irreflexiv ist. Aus
demselben Grund ist auch "x ∈∈ y ˄ y ∈∈ x"
immer eine falsche Aussage, denn mit x ∈∈ y ˄ y ∈∈ x
würde wegen der Transitivität von ∈∈ω die
falsche Aussage "x ∈∈ x" folgen.
Für x, y ∈∈ ω
schreibt man üblicherweise "x < y"
statt "x ∈∈ y".
Es ist also entweder x < y
oder y < x oder x = y, das heißt: je zwei Elemente von
ω sind vergleichbar. Da alle Elemente von ω transitive Mengen sind, folgt aus x < y
stets x ⊂ y.
Definiert man die Identitätsrelation auf einer Menge m durch
idm =def { g ∈∈ m x m | λ(g) = ρ(g) }
und die Teilmengenrelation auf einer Menge m durch
⊆m =def { g ∈∈ m x m | λ(g) ⊆ ρ(g) },
dann gilt
∈∈ω ∪ idω =
⊆ω.
Beweis:
Gemäß EXT hat man ∈∈ω ∪ idω ⊆ ⊆ω
und ⊆ω ⊆ ∈∈ω ∪ idω nachzuweisen.
(i) zu zeigen: ∈∈ω ∪ idω ⊆ ⊆ω.
Aus (x; y) ∈∈ ∈∈ω ∪ idω folgt
x ∈∈ y ˅ x = y.
Mit TM ergibt sich x ⊆ y,
das heißt: (x; y) ∈∈ ⊆ω.
(ii) zu zeigen:
⊆ω ⊆ ∈∈ω ∪ idω
Die Aussage "(x; y) ∈∈ ⊆ω ⇀ (x; y) ∈∈ ∈∈ω ∪ idω"
ist äquivalent zu "(x; y) ∉∉ ∈∈ω ∪ idω ⇀ (x; y) ∉∉ ⊆ω".
Sei (x; y) ∉∉ ∈∈ω ∪ idω
⇒ x ∉∉ y ˄ x ǂ y
⇒ y ∈∈ x
(wegen der Konnexität von ∈∈ω)
⇒ y ⊆ x (wegen TM)
Angenommen, es gilt (x; y) ∈∈ ⊆ω.
⇒ x ⊆ y ˄ y ⊆ x
⇒ x = y. Widerspruch!
Es gilt also (x; y) ∉∉ ⊆ω,
was zu zeigen war.
Wegen ∈∈ω ∪ idω =
⊆ω wird statt „x ⊆ y“ für x,y ∈∈ ω
meist „x ≤ y“
geschrieben.
![]() N5
N5
Sei x ∈∈ ω
beliebig gewählt. Dann gilt x < s(x)
und es existiert kein e ∈∈ ω
mit x < e < s(x).
Beweis:
Es gilt x ∈∈ { x }
und damit auch x ∈∈ x ∪ { x },
was x < s(x)
bedeutet.
Es gibt kein e ∈∈ ω
mit e ∈∈ Ø, also ist Ø bezüglich
„<“ das kleinste Element von ω.
Wegen s(Ø) = { Ø } gilt Ø <
s(Ø). Ø ist das einzige Element von s(Ø)
und damit das einzige Element, was kleiner ist als s(Ø).
Sei nun m ∈∈ ω
mit m ǂ Ø, aber ansonsten beliebig gewählt.
Angenommen, es gibt ein e ∈∈ ω
mit m < e < s(m).
m < e
ist gleichbedeutend mit m ∈∈ e.
Wegen e ∈∈ ω
existiert ein x ∈∈ ω mit
e = x ∪ { x }
und x < e.
Dann ist entweder m ∈∈ x
oder m = x.
Im Fall "m = x" hat man e = m ∪ { m } = s(m).
Widerspruch zur Annahme!
Im Fall "m ∈∈ x"
folgt mit N3 s(m) ∈∈ x ˅ s(m) = x.
Mit s(m) ∈∈ x ergibt sich
s(m) < e <
s(m).
Hieraus folgt s(m) <
s(m)
(wegen der Transitivität von ∈∈ω)
und dies ist eine falsche Aussage wegen der Irreflexivität von ∈∈ω.
Aus s(m) = x folgt die falsche Aussage "x < e < x".
Die obige Annahme kann demnach nicht richtig sein, woraus die Behauptung folgt.
Die Nachfolgerfunktion trägt also ihren Namen zu Recht: Ist x ∈∈ ω,
so folgt s(x) auf x bezüglich „<“
unmittelbar. s(x)
heißt Nachfolgermenge (oder kurz: Nachfolger) von x. xp heißt Vorgängermenge (oder kurz:
Vorgänger) von x, wenn s(xp) = x.
![]() N6
N6
Jedes Element n von ω umfasst alle diejenigen Elemente von
ω, die kleiner sind als n:
n = { x ∈∈ ω | x <
n } für alle n ∈∈ ω.
Beweis:
Sei n ∈∈ ω. Wegen x ∈∈ n ⇌
x <
n folgt n = { x ∈∈ ω | x < n }
unmittelbar.
![]() N7
N7
Mit ∈∈ω ∪ idω
ist ω wohlgeordnet.
Beweis:
Seien x, y, z ∈ ω beliebig gewählt.
(i) zu zeigen: x ≤ y ˄ y ≤ z ⇀ x ≤ z (Transitivität).
∈∈ω und idω
sind transitiv, also auch ∈∈ω ∪ idω.
(ii) zu zeigen: x ≤ y ˄ y ≤ x ⇀ x = y (Identitivität).
Da die Aussagen "x < y"
und "y < x" sich
gegenseitig ausschließen,
folgt aus x ≤ y ˄ y ≤ x,
dass x und y gleich sein müssen.
(iii) zu zeigen: x ≤ x (Reflexivität).
Die Aussage "x ≤ x"
ist wahr, weil x = x immer gilt.
(iv) zu zeigen: x ≤ y ˅ y ≤ x (Konnexität).
(v) zu zeigen: Jede nichtleere Teilmenge von ω hat bezüglich
„≤“ ein kleinstes Element.
Sei t ⊆ ω mit t ǂ Ø.
Im Fall t = ω ist Ø das kleinste Element.
Alle t ⊆ ω
mit Ø ∈∈ t haben demnach auch Ø als kleinstes Element.
Für alle t ⊂ ω
mit Ø ∉∉ t gilt
∩t ǂ Ø,
denn die Durchschnittsmenge
∩t umfasst alle Objekte, die Element von jedem Element von t
sind und wegen Ø ∉∉ t ist
Ø ∈∈ n für alle n ∈∈ t.
∩t enthält
also mindestens Ø als Element. Somit gibt es ein n* ∈∈ ∩t
mit s(n*) ∉∉ ∩t
(wäre es nicht so, würde die offensichtlich falsche Aussage
∩t = ω
folgen). Also hat man ∩t = s(n*) = { x ∈∈ ω | x ≤ n* }. Hieraus ergibt
sich s(n*) ≤ e für alle e ∈∈ t.
Nun ist aber s(n*) ∉∉ ∩t,
also muss s(n*) ∈∈ t
gelten, womit s(n*) als kleinstes Element von t gefunden ist.
Der nächste Satz besagt, dass Funktionen auf ω rekursiv definiert werden können:
![]() N8 (Rekursionssatz für ω)
N8 (Rekursionssatz für ω)
Sei F ein Operator. Dann gibt es genau eine auf ω
definierte Funktion f mit
RK ∀n∈∈ω (f(n) = F(f|n)).
Beweis:
RK kann man unter Verwendung von ERS umformulieren zu folgender Aussage:
RK* f(Ø) = Ø ˄ f(s(n)) = F({ (x; f(x) | x ≤ n })
für alle n ∈∈ ω.
Hierbei beachte man, dass f|Ø = Ø, weil Ø keine Elemente besitzt.
(i) zu zeigen: Es gibt höchstens eine Funktion, die RK erfüllt.
Seien f und g zwei Funktionen, die RK* erfüllen.
zu zeigen: f = g,
das heißt: f(n) = g(n) für alle n ∈∈ ω.
Zunächst gilt f(Ø) = g(Ø) und hieraus folgt
f({ Ø })
=
F({ (Ø; g(Ø)) })
=
g({ Ø })
=
und für beliebiges n ∈∈ ω:
f(s(n))
=
F({ (x; g(x) | x ≤ n })
=
g(s(n)).
=
(ii) zu zeigen: Es gibt eine Funktion f mit den geforderten Eigenschaften.
Hierzu wird definiert: a ist genau dann ein echtes Anfangsstück von
ω (kurz: „a:EAS“), wenn
a ⊂ ω
mit ∀n,m∈∈a (m < n ˄ n ∈∈ a ⇀ m ∈∈ a).
Sei 𝑭a die
Klasse aller Funktionen f mit dom(f):EAS und f(n) = F(f|n)
für alle n ∈∈ dom(f).
Auf jeden Fall ist 𝑭a
nicht leer, denn wegen f(Ø) = F(Ø) ist (Ø; F(Ø)) ∈∈ 𝑭a.
Mit beliebig gewählten f1,f2 ∈∈ 𝑭a
ist dann entweder dom(f1) ⊆ dom(f2)
oder dom(f2) ⊆ dom(f1).
Ohne Beschränkung der Allgemeinheit sei dom(f1) ⊆ dom(f2).
Wegen Ø ∈∈ dom(f1)
folgt analog zur Argumentation unter (i)
f1(Ø) = f2(Ø)
und darüberhinaus f1(n) = f2(n)
für alle n ∈∈ dom(f1).
Damit hat man f1 ⊆ f2,
also ist 𝑭a eine Funktionenkette.
Wegen R1 ist auch v =def
⋃𝑭a
eine Funktion und es gilt dom(v) = ⋃{ dom(f) | f ∈∈ 𝑭a }.
dom(v) ist als Vereinigung echter Anfangsstücke ebenso ein echtes Anfangsstück.
zu zeigen: v(n) = F(v|n)
für alle n ∈∈ dom(v).
Wenn n ∈∈ dom(v),
so existiert f ∈∈ 𝑭a
mit n ∈∈ dom(f).
Sowohl dom(f) als auch dom(v) sind echte
Anfangsstücke und es ist f ⊆ v,
also gilt f|n = v|n
und damit v(n) = f(n) = F(f|n) = F(v|n).
Somit ist v ∈∈ 𝑭a und zwar mit der Eigenschaft, dass
(*) f ⊆ v für alle f ∈∈ 𝑭a.
Angenommen, dom(v) ǂ ω.
Dann hat ω\dom(v), die Differenz von ω und
dom(v), als Teilmenge der
wohlgeordneten Menge ω ein kleinstes Element, das mit n* bezeichnet werden soll. Mit
dom(v) ∪ { n* }
erhält man gemäß ERS v* = v ∪ { (n*; F(v)) } als Fortsetzung von v.
Daraus folgt v* ∈∈ 𝑭a
und v ⊆ v*. Widerspruch zu (*)!
Es folgt also dom(v) = ω, was noch zu beweisen war.
![]() N9 (Einfacher Rekursionssatz für ω)
N9 (Einfacher Rekursionssatz für ω)
Sei F ein Operator und c eine beliebige Menge.
Dann gibt es genau eine auf ω definierte Funktion f
mit
f(Ø) = c
∀n∈∈ω (f(s(n)) = F(f(n))).
Beweis:
Sei F ein Operator, c eine beliebige Menge und n ∈∈ ω.
Dann ist G, definiert durch
G(x) =def F(x(n)),
falls x ∈∈ 𝑭 ˄ dom(x) = s(n);
c sonst
ebenfalls ein Operator und es existiert nach dem Rekursionssatz für ω genau eine Funktion f auf ω, so dass
f(n) = G(f|n) für alle n ∈∈ ω.
Hieraus folgt mit Ø ∈∈ 𝑭 ˄ dom(Ø) = Ø ˄ ∄n (Ø = s(n))
f(Ø) = G(Ø) = c.
Wegen f ∈∈ 𝑭 ˄ s(n)
⊆
ω hat man f|s(n) ∈∈ 𝑭 ˄ dom(f|s(n)) = s(n).
Damit ergibt sich
f(s(n)) = G(f|s(n)) = F(f(n))
für alle n ∈∈ ω.
Aus N9 folgt der Spezielle Rekursionssatz für ω, dessen Aussage dem Satz der Definition durch Induktion von Richard Dedekind entspricht (Nummer 126 in: Was sind und was sollen die Zahlen?):
![]() N10 (Spezieller Rekursionssatz für ω)
N10 (Spezieller Rekursionssatz für ω)
Sei m eine nichtleere Menge,
c ∈∈ m
und h: m → m. Dann gibt
es genau eine Funktion f mit
f: ω → m
f(Ø) = c
∀n∈∈ω (f(s(n)) =
h(f(n)).
Beweis:
Sei m eine beliebige nichtleere Menge, c ∈∈ m, h: m → m und F speziell gewählt:
F(x) =def h(x),
falls x ∈∈ m; Ø sonst.
Dann gilt F(x) = h(x) für alle x ∈∈ m
und es gibt gemäß N9 genau eine Funktion f mit
f(Ø) = c ˄ f(s(n)) = F(f(n))
für alle n ∈∈ ω.
Es ist f(Ø) ∈∈
m und mit f(n) ∈∈
m ist wegen F(f(n)) = h(f(n)) = f(s(n))
auch f(s(n)) ∈∈ m.
Damit hat man rng(f) ⊆ m und so auch
f(s(n)) = F(f(n)) = h(f(n))
für alle n ∈∈ ω.
![]() N11
N11
Je zwei Peano-Strukturen sind isomorph zueinander.
Beweis:
Nach N1 ist
(ω,s,Ø) eine Peano-Struktur. Sei (w,σ,o) eine
weitere Peano-Struktur. Dann ist w gemäß Axiom (I)* nicht leer und es gibt
aufgrund des eben bewiesenen speziellen Rekursionssatzes eine eindeutig bestimmte Funktion f, so dass das Folgende gilt:
f: ω → w
f(Ø) = o
∀n∈∈ω (f(s(n)) =
σ(f(n)).
f ist dann ein Isomorphismus, wenn
gezeigt werden kann, dass f eine Bijektion ist.
zu zeigen: (i)
f: ω sur→ w. und (ii) f: ω inj→ w.
(i) (w,σ,o) erfüllt als Peano-Struktur das Axiom (IV)*:
∀t⊆w (o ∈∈ t ˄ ∀x∈∈t (σ(x) ∈∈ t) ⇀ t = w).
Es gilt rng(f) ⊆ w
und es ist o ∈∈ rng(f).
Für jedes x ∈∈ rng(f)
existiert ein n ∈∈ ω
mit x = f(n).
Es folgt also σ(x) = σ(f(n)) = f(s(n)) ∈∈ rng(f)
und damit hat man mit (IV)*: rng(f) = w, was zu zeigen war.
(ii)
zu zeigen:
∀n∈∈ω (∀x∈∈ω (x ǂ n ⇀ f(x) ǂ f(n))).
Induktionsanfang:
Sei n = Ø. f(Ø) = o
und o ∉∉ rng(σ)
gemäß Axiom (III)*.
Wenn x ǂ Ø, so
hat x eine Vorgängermenge xp, das heißt: x = s(xp).
f(x) = σ(f(xp)),
also f(x) ∈∈ rng(σ).
Insgesamt folgt demnach f(x) ǂ f(Ø).
Induktionsvoraussetzung:
Es gelte ∀x∈∈ω (x ǂ m ⇀ f(x) ǂ f(m))
für ein beliebig gewähltes m ∈∈ ω.
Induktionsschluss:
Sei x ǂ s(m).
Falls x = Ø folgt analog zum Induktionsanfang f(Ø) ǂ f(s(m)).
Sei also x ǂ Ø,
mit anderen Worten: x = s(xp).
Wegen s(xp) ǂ s(m)
hat man xp ǂ m,
weil s ∈∈ 𝑭.
Mit der Induktionsvoraussetzung folgt f(xp) ǂ f(m) und damit σ(f(m)) ǂ σ(f(xp))
wegen σ: w inj→ w gemäß (II)*.
f(s(m) = σ(f(m)).
f(x) = f(s(xp)) =
σ(f(xp)).
Mit σ(f(xp)) ǂ σ(f(m))
folgt f(x) ǂ f(s(m), was zu zeigen war.
Es ist bemerkenswert, dass für den vorstehenden Beweis alle Peano’schen Axiome benötigt werden. Außerdem ist hervorzuheben, dass die Tatsache, dass (ω,≤) eine Wohlordnung ist, bewiesen werden kann, ohne zuvor eine innere Verknüpfung auf ω definiert zu haben! Plakativ ausgedrückt: Man kann mit den Elementen von ω zählen ohne rechnen zu müssen. Das ist in ℕ anders.
N11 besagt, dass die den Peano’schen Axiomen genügende Struktur bis auf Isomorphie eindeutig bestimmt ist. Das Peano’sche Axiomensystem ist also monomorph (oder kategorisch).
Wegen (ω,s,Ø) ≅ (ℕ,succ,0)
ist es nunmehr sinnvoll, die vonNeumann’schen Zahlen
mit Hilfe der gewöhnlichen natürlichen Zahlen zu bezeichnen: 0 =def Ø, 1 =def { Ø },
2 =def { Ø, { Ø } }, ...,
s(n) =def n ∪ { n }
und es
gilt für beliebiges n ∈∈ ω und die Nachfolgermenge
s(n) :
s(n) = { 0, 1, ..., n
}.
Unter Benutzung dieser Bezeichnungen lässt sich auf ω eine Addition und eine Multiplikation definieren. Diese beiden zweistelligen Verknüpfungen haben die folgenden Eigenschaften:
(i) s(n) = n
+ 1
(ii) n + 0 = n
(iii) m + (n + 1) = (m
+ n) + 1
(iv) n · 0 = 0
(v) m · (n + 1) = m
+ (m
· n)
Beweis:
Sei n ∈∈ ω
beliebig, aber fest gewählt. Dann gibt es nach dem speziellen Rekursionssatz für
ω genau eine
Funktion addn mit
addn: ω → ω
addn(0) = n
∀m∈∈ω (addn(s(m)) =
s(addn(m))).
Sei r+ =def { x ∈∈ (ω x
ω) x ω
| ρ(x) = addλ(λ(x))(ρ(λ(x))) },
einfacher geschrieben: r+ = { ((n; m); k) | k = addn(m) }.
r+ ∈∈ 𝑭, denn r+|{n}xω ∈∈ 𝑭 für
alle n ∈∈ ω
wegen r+|{n}xω(n; m) = addn(m)
für alle n,m ∈∈ ω.
(i) n
+ 1 = addn(s(0)) =
s(addn(0)) =
s(n).
(ii) n
+ 0 = addn(0) = n.
(iii) m + (n + 1) = addm(s(n)) =
s(addm(n)) =
s(m
+ n) = (m
+ n) + 1.
Zu jedem n ∈∈ ω gibt es neben addn auch genau eine Funktion muln mit
muln: ω → ω
muln(0) = 0
∀m∈∈ω (muln(s(m)) = addn(muln(m))).
Sei r· =def { x ∈∈ (ω x
ω) x ω
| ρ(x) = mulλ(λ(x))(ρ(λ(x))) },
einfacher geschrieben: r· = { ((n; m); k) | k = muln(m) }.
Analog zu oben gilt r· ∈∈ 𝑭.
(iv) n · 0 = muln(0) = 0.
(v) m · (n + 1) =
mulm(s(n)) = addm(mulm(n)) = m + (m · n).
Die bekannten Rechengesetze bezüglich „+“ und „·“, wie Kommutativ-, Assoziativ- und Dissoziativgesetze erschließt man sich durch Induktionsbeweise: vgl. Addieren und Multiplizieren natürlicher Zahlen.
Üblicherweise nennt man eine Menge genau dann endlich, wenn man die Elemente dieser Menge mit Hilfe der natürlichen Zahlen abzählen kann. Es ist jedoch durchaus möglich, den Begriff „endliche Menge“ ohne Verwendung der natürlichen Zahlen zu definieren:
Sei a eine Menge, ℘(a)
die Potenzmenge von a und u ⊆ ℘(a)
eine Teilmenge von ℘(a).
u ist ein induktives System in ℘(a)
(kurz formuliert: „u:IND(a)“) genau dann, wenn
Ø ∈∈ u ˄ ∀t∈∈u ∀x∈∈a\t
(t ∪ { x } ∈∈ u).
Es folgt unmittelbar, dass ℘(a):IND(a)
für alle a gilt. Das heißt, es existiert immer mindestens ein induktives System in
℘(a),
nämlich ℘(a) selbst.
Eine Menge a ist genau dann endlich,
falls ℘(a)
das einzige induktive System in ℘(a) ist.
𝑬 sei die Klasse aller endlichen Mengen.
Diese auf den ersten Blick möglicherweise irritierende Definition versteht man besser, wenn man sich deren anschauliche Bedeutung klarmacht. Man stelle sich einen Haufen mit
beliebig vielen Objekten vor, wobei man zunächst nicht weiß, ob es sich hierbei um endlich viele Objekte handelt oder nicht. Nun nehme man sukzessiv Objekte
aus dem Haufen heraus, in jedem Schritt jeweils ein Objekt. Endet dieser Wegnehme-Prozess irgendwann damit, dass der Haufen einmal gänzlich
weg ist, weiß man: der Haufen bestand aus endlich vielen Objekten. Sei nun beispielsweise a = { u, v }
(eine augenscheinlich endliche Menge :). Dann sind { Ø, { u }, { u, v } } und
{ Ø, { v }, { u, v } }
Teilmengen von ℘(a) und repräsentieren die zwei kompletten und möglichen Wegnehme-Prozesse bei
einem gegebenen Haufen mit zwei Objekten. Jedes Element von
℘(a)
schließlich repräsentiert einen Zustand des (endlichen) Haufens während eines der möglichen Wegnehme-Prozesse. Und: für jeden dieser möglichen
Zustände gibt es ein entsprechendes Element in ℘(a).
Aus der obigen Definition folgt sofort ein zwar trivialer, aber nichtsdestoweniger wichtiger Satz:
![]() E1
E1
Die leere Menge ist endlich.
Der nächste Satz ist grundlegend für viele Beweise von Aussagen über endliche Mengen.
![]() E2
E2
Sei a eine endliche Menge und b ∉∉ a.
Dann ist auch
a ∪ { b } endlich.
Beweis:
Sei a eine endliche Menge, b ∉∉ a
und u* ein induktives System in ℘(a ∪ { b }).
Mit u =def { t ∈∈ u* | t ⊂ a }
folgt u:IND(a).
Weil a endlich ist, gilt u = ℘(a).
Da u nach Definition eine echte Teilmenge von u* ist, folgt
(1) ℘(a) ⊂ u*.
Wegen u*:IND(a ∪ { b })
gilt ∀t∈∈u* ∀x∈∈a∪{ b }\t
(t ∪ { x } ∈∈ u*).
Insbesondere gilt also (2) ∀t∈∈℘(a) (t ∪ {
b } ∈∈ u*).
Aus (1)˄(2) folgt
℘∪ { b })
=
℘(a) ∪ { t ∪ { b } | t ∈∈ ℘(a) }
⊆
und weil andererseits u* ⊆ ℘(a ∪ { b })
gilt u* = ℘(a ∪ { b }).
Daraus folgt, dass a ∪ { b } endlich ist.
![]() E3
E3
a ist genau dann endlich, wenn jedes induktive System in ℘(a) a
enthält.
Beweis:
„⇀“:
Sei a eine endliche Menge. Dann ist ℘(a)
das einzige induktive System in ℘(a)
und es gilt a ∈∈ ℘(a).
„↽“:
Angenommen, a ∈∈ u, falls
u:IND(a).
Sei u* =def {
t ∈∈ ℘(a) | t ∈∈ 𝑬 }.
Dann ist Ø ∈∈ u* wegen E1.
Falls t ∈∈ u* und x ∈∈ a\t,
so folgt t ∪ { x } ∈∈ u*
wegen E2.
Damit ist aber u*:IND(a).
Wegen a ∈∈ u* (aufgrund der getroffenen Annahme) folgt a ∈∈ 𝑬.
![]() E4
E4
Sei a eine endliche Menge und t ⊂ a
eine echte Teilmenge von a. Dann ist auch t endlich.
Beweis:
Sei a ∈∈ 𝑬 und
u =def { t ∈∈ ℘(a) | t ∈∈ 𝑬 }.
∀t∈∈u ∀x∈∈a\t (t ∪ {
x } ∈∈ u) wegen E2 und es ist Ø ∈∈ u
wegen E1.
Dies ist gleichbedeutend mit u:IND(a), also u = ℘(a),
mit anderen Worten: ∀t⊂a (t ∈∈ 𝑬).
Sei φ ein Prädikat und m eine endliche Menge. Dann soll im Folgenden mit „φm“ die Aussage „φ(m) trifft zu“ gemeint sein. „φE“ bedeutet „φ trifft zu für alle Mengen, die endlich sind“.
![]() E5
E5
Sei φ ein Prädikat, das eine gewisse Eigenschaft endlicher
Mengen beschreibt. Wenn die leere Menge diese Eigenschaft besitzt und ferner für eine beliebige endliche Menge
m neben φm auch φm∪{b}
für alle b ∉∉ m gilt, so besitzt jede endliche Menge diese Eigenschaft:
φØ ˄ ∀m∈∈𝑬 ∀b∉∉m (φm ⇀ φm∪{b}) ⇀ φE
Beweis:
Sei φ ein Prädikat mit φØ, m eine
endliche Menge und b ∉∉ m.
Es gelte unter diesen Bedingungen φm ⇀ φm∪{b},
das heißt, wenn φ für m zutrifft, so auch für
m∪{b}.
Sei nun a eine beliebig gewählte endliche Menge.
Mit u =def {
t ∈∈ ℘(a) | φt }
hat man dann zunächst Ø ∈∈ u.
Wegen E4 gilt t ∈∈ 𝑬 für jedes t ∈∈ u.
Nach Voraussetzung gilt demnach auch φt∪{b} falls
t ∈∈ u und b ∈∈ a\t.
Dann gilt mit t ∈∈ u auch t∪{b} ∈∈ u.
Also folgt u:IND(a).
Wegen a ∈∈ 𝑬 hat man
u = ℘(a).
Hieraus folgt a ∈∈ u
weil a ∈∈ ℘(a).
Also gilt φa.
Demnach trifft φ für alle endlichen Mengen zu, denn a war beliebig gewählt.
![]() E6
E6
Alle vonNeumann’schen Zahlen sind endlich:
n ∈∈ ω ⇀ n ∈∈ 𝑬
Beweis:
Induktionsanfang:
Ø ∈∈ 𝑬.
Induktionsvoraussetzung:
Es gelte m ∈∈ 𝑬 für ein gewisses m ∈∈ ω.
Induktionsschluss:
s(m) = m ∪ { m }.
m ∉∉ m. Also folgt
mit E2 s(m) ∈∈ 𝑬 und damit die Behauptung.
![]() E7
E7
Eine Menge a ist genau dann endlich, wenn ein n ∈∈ ω
existiert, so dass n und a gleichmächtig sind.
Kurz geschrieben:
a ∈∈ 𝑬 ⇌ ∃n (n ∈∈ ω ˄ a ∼ n).
Beweis:
„⇀“:
Es gilt Ø: 0 bij→ Ø, in Worten: die leere Funktion bildet 0 bijektiv auf die leere Menge ab.
Sei nun a eine beliebig gewählte endliche Menge,
für die es ein n ∈∈ ω
gibt mit a ∼ n.
Dann existiert f mit f: n bij→ a.
Mit N6 folgt f = { (x; f(x)) | x = 0
.. np }.
Sei nun b eine beliebige Menge mit b ∉∉ a.
Mit VER hat man f* =def f ∪ { (n; b) }
und damit f*: a∪{b} bij→ s(n).
Wegen E5 folgt: Für alle endlichen Mengen a gibt es
ein n ∈∈ ω mit a ∼ n.
„↽“:
Sei n ∈∈ ω und a eine Menge mit a ∼ n.
Also gibt es ein f mit f: n bij→ a, das heißt:
a = { ai | i = 0 .. np } mit ai =def f(i) für
i ∈∈ n.
Sei u ⊆ ℘(a) mit
u:IND(a) und sei t ∈∈ u.
Dann ist a\t = { aj | j < n ˄ aj ∉∉ t }.
Umnummerierung liefert a\t = { aj | j = 0 .. k } mit einem gewissen k < n.
Sei t0 =def t
und tj+1 =def tj ∪ {
aj } für j = 0 .. k.
Dann gilt { tj | j = 0
.. k } ∈∈ u wegen
u:IND(a).
Da a = { tj | j = 0
.. k } folgt a ∈∈ 𝑬 wegen E3.
Sei a endlich. Dann existiert also eine Bijektion f: n bij→ a mit n ∈∈ ω. Eine solche Bijektion heißt Abzählung von a der Länge n.
![]() E8
E8
Sei a eine endliche Menge. Dann haben alle Abzählungen von a dieselbe Länge.
Beweis:
Wegen x ∼ y ˄ y ∼ z ⇀ x ∼ z ist
die zu beweisende Aussage äquivalent zu:
ZS ∀n,k∈∈ω (n ∼ k ⇀
n = k).
ZS lässt sich durch Induktion über n beweisen.
Induktionsanfang:
Aus n = Ø ˄ n ∼ k folgt
n = Ø = k.
Induktionsvoraussetzung:
Es gelte m ∼ k ⇀ m = k
für ein beliebig gewähltes m ∈∈ ω.
Induktionsschluss:
Sei f: s(m) ∼ k. Dann ist k ǂ Ø
und k = s(kp).
Falls f(m) ǂ kp,
sei π diejenige Permutation von k, die f(m) und kp
miteinander vertauscht;
falls f(m) = kp,
sei π = idk.
Dann folgt π∘f: s(m) ∼ k ˄ (π∘f)(m) = kp
und damit hat man π∘f \ { (m; kp) }: m ∼ kp.
Mit der Induktionsvoraussetzung folgt m = kp, also gilt s(m) = s(kp) = k,
was zu zeigen war.
Der eben bewiesene Satz ermöglicht die folgende Definiton:
Sei a eine endliche Menge und n ∈∈ ω mit
a ∼ n.
Dann ist n die Mächtigkeit von a (in Zeichen: „|a| = n“).
Demnach sind endliche Mengen genau dann äquivalent, wenn sie die gleiche Mächtigkeit haben.
Für n ∈∈ ω gilt |n| = n.
![]() E9
E9
Sei a eine endliche Menge und t ⊂ a
eine echte Teilmenge von a. Dann
gilt |t| < |a|.
Beweis:
(i) zunächst zu zeigen: ∀n∈∈ω ∀t (t ⊂ n ⇀ |t| < n).
Induktionsanfang:
Ø besitzt keine echte Teilmenge.
Also ist für n = Ø nichts nachzuweisen.
Induktionsvoraussetzung:
Es gelte ∀t (t ⊂ m ⇀ |t| < m)
für ein gewisses m ∈∈ ω.
Induktionsschluss:
Sei t eine beliebige echte Teilmenge von s(m).
Dann ist entweder m ∈∈ t
oder m ∉∉ t.
Aus m ∈∈ t folgt
s(m) ⊆ t
im Widerspruch zu t ⊂ s(m).
Es gilt also m ∉∉ t.
Hieraus folgt mit N6 t ≤ m,
was t ⊆ m bedeutet.
Wenn t = m, so folgt
|t| = m < s(m).
t ⊂ m
liefert
|t| < m < s(m)
nach Induktionsvoraussetzung.
(ii) Sei nun a ∈∈ 𝑬 ˄ t ⊂ a.
Wegen a ∈∈ 𝑬 gibt es ein n ∈∈ ω
mit |a| = n,
das heißt, es existiert eine Funktion f, so dass f: n bij→ a.
Somit existiert auch f−1, so dass f−1: a bij→ n.
Ausserdem gilt f−1|t: t bij→ x
mit x ⊂ n wegen t ⊂ a.
Mit der unter (i) bewiesenen Aussage folgt |x| < n
und hiermit |t| < |a|
wegen t ∼ x und a ∼ n.
![]() E10
E10
Seien a und b endlich und disjunkt, also a ∩ b = Ø.
Dann ist auch a ∪ b
endlich und es gilt |a ∪ b| = |a| + |b|.
Beweis:
Wenn a = Ø ˅ b = Ø,
so ist die behauptete Aussage offensichtlich wahr.
Seien also beide Mengen a und b endlich und nicht leer und a ∩ b = Ø.
Dann existieren zwei Funktionen f und g, so dass
f: n bij→ a und g: m bij→ b
mit 0 < n und 0 < m.
Gemäss VER hat man die Menge h = f ∪ g,
deren Elemente nach ERS unter
Verwendung des folgenden Operators ersetzt werden können:
F((i; x)) =def (i; x),
falls x ∈∈ a;
(i+n; x), falls x ∈∈ b;
0 sonst.
Es ist F(h): n+m bij→ a ∪ b.
Damit folgt die behauptete Aussage.
![]() E11
E11
Für zwei endliche Mengen a und b
gilt |a| + |b| = |a ∪ b| + |a ∩ b|.
Beweis:
Sei a,b ∈∈ 𝑬 und x =def a ∩ b
und y =def a\x = a\b.
Wegen x ⊆ a und
y ⊆ a folgt x,y ∈∈ 𝑬 und es gilt
(1) a ∪ b = y ∪ b,
wobei y ∩ b = Ø und
(2) a = x ∪ y,
wobei x ∩ y = Ø.
Aus (1) folgt: (y ∪ b) ∈∈ 𝑬
und |a ∪ b| = |y| + |b|
und aus (2): |a| = |x| + |y| = |a ∩ b| + |y|.
Hieraus folgt die Behauptung.
![]() E12
E12
Für zwei endliche Mengen a
und b gilt a x b ∈∈ 𝑬
und |a x b| = |a|·|b|.
Beweis:
Wenn a = Ø ˅ b = Ø,
so ist die behauptete Aussage offensichtlich wahr.
Seien also beide Mengen a und b endlich und nicht leer.
Dann existieren zwei Funktionen f und g, so dass
f: n bij→ a und g: m bij→ b
mit 0 < n und 0 < m.
Sei fi =def { (v; x) ∈∈ f | v = i } für
i = 0, 1, ..., np.
Die fi sind gemäß AUS (einelementige) Mengen:
fi = { (i; f(i)) }.
Mit ERS gelangt man zu den Mengen { f(i) };
i = 0, 1, ..., np.
Mit bi =def { f(i) } x b
gilt |bi| = m für
i = 0, 1, ..., np.
Alle diese bi sind paarweise disjunkt, also folgt
|a x b| = |b0 ∪ b1 ... ∪ bnp| = n·m,
was zu beweisen war.
![]() E13
E13
ω ist keine endliche Menge.
Beweis:
Angenommen, ω ist endlich.
Dann existiert nach E7 ein n ∈∈ ω
mit ω ∼ n.
n ist gemäß E8 eindeutig
bestimmt und es gilt |ω| = n.
Nach N6 umfasst n alle
x ∈∈ ω
mit x < n.
Demnach ist n ⊂ ω
und es gilt |n| = n = |ω|.
Dies ist ein Widerspruch zu E9,
also ist ω unendlich.
Fundierte Strukturen und Wohlordnungen
![]()
Sei m eine nichtleere Menge und r eine Relation auf m. Dann
nennt man die Struktur (m,r)
fundiert (und m eine fundierte Menge)
genau dann, wenn jede nichtleere Teilmenge von m ein r-minimales Element
besitzt, das heißt, wenn für jede nichtleere Teilmenge a ⊆ m
das Folgende gilt:
∃b (b ∈∈ a ˄ a ∩ r[b] = Ø).
Hierbei ist r[b] die Menge aller r-Vorgänger von b:
r[b] =def {
v ∈∈ dom(r) | v r
b }.
Es gilt der Induktionssatz für fundierte Strukturen:
![]() W1 (Induktionssatz für fundierte Strukturen)
W1 (Induktionssatz für fundierte Strukturen)
Wenn (m,r) eine fundierte Struktur ist, so gilt
∀a (∀x∈∈m (r[x]⊆a ⇀ x∈∈a) ⇀ m ⊆ a).
Beweis:
Sei
(m,r) eine fundierte Struktur und
es gelte (*) ∀x∈∈m
(r[x] ⊆ a ⇀ x ∈∈ a).
Angenommen, a ist hierbei eine Menge mit m\a ǂ Ø.
m\a hat als Teilmenge von m ein r-minimales Element
v.
Hieraus folgt gemäß Annahme r[v] ⊆ a
und damit
v ∈∈ a nach Voraussetzung (*).
Widerspruch!
Also gilt (*) für alle a, was zu zeigen war.
Sei (m,r) eine fundierte Struktur und φ ein
einstelliges Prädikat. Dann folgt mit a = { x ∈∈ m | φ(x) } aus W1,
dass
∀b∈∈m (∀x (x r b ⇀ φ(x)) ⇀ φ(b)) ⇀ ∀b∈∈m (φ(b)).
Mit dem Fundierungsaxiom (FND) folgt, dass (m,∈∈m) eine fundierte Struktur ist. FND garantiert also, gegebenenfalls induktiv über ∈∈m beweisen zu können, dass alle Elemente einer gegebenen Menge eine gewisse Eigenschaft haben.
Ist (m,r) eine fundierte Struktur und m bezüglich r
linear geordnet, dann
nennt man (m,r) eine Wohlordnung. m heißt Trägermenge (oder kurz:
Träger) von (m,r) und man sagt: „m ist mit r
wohlgeordnet“. 𝑾 sei die
Klasse aller Wohlordnungen.
Sei (m,r) eine Wohlordnung. Dann heißt eine Teilmenge
a ⊆ m
Anfangsstück von m bezüglich r genau dann, wenn
b ∈∈ a
⇀
r[b] ⊆ a.
Ist a ein
Anfangsstück von m bezüglich r und b = r ∩ axa, so
heißt (a,b) Anfangsabschnitt von (m,r).
Ist a ein Anfangsstück von m bezüglich r und a ǂ m, so nennt man a ein echtes Anfangsstück und der zugehörige Anfangsabschnitt heißt echter Anfangsabschnitt.
Ein Anfangsabschnitt einer Wohlordnung ist immer wohlgeordnet.
![]() W2
W2
(m,r) und (m*,r*) seien Wohlordnungen. Sind f
und g Isomorphismen von
(m,r) auf Anfangsabschnitte von (m*,r*), so gilt f = g.
Beweis:
Seien (m,r) und (m*,r*) Wohlordnungen und u ∈∈ m.
Ist f ein Isomorphismus von (m,r) auf einen Anfangsabschnitt von (m*,r*),
so ist f(u) das r*-minimale Element von m*\rng(f|r[u]),
denn u ist das r-minimale Element von m\r[u].
Sei nun g ebenfalls ein Isomorphismus von (m,r) auf einen Anfangsabschnitt von (m*,r*) mit der Eigenschaft, dass
f|r[u] = g|r[u].
Dann ist g(u) das r*-minimale Element von m*\rng(g|r[u]) und es folgt
f(u) = g(u),
denn das minimale Element einer Menge ist natürlich eindeutig bestimmt.
Da u ∈∈ m beliebig gewählt war, folgt mit W1 die Behauptung.
Es folgt sofort, dass, wenn es zwischen zwei Wohlordnungen einen Isomorphismus geben sollte, dieser eindeutig bestimmt ist. Ferner folgt aus W2
![]() W3
W3
Es gibt keinen Isomorphismus von einer Wohlordnung auf einen ihrer echten Anfangsabschnitte.
![]() W4 (Vergleichbarkeitssatz für Wohlordnungen)
W4 (Vergleichbarkeitssatz für Wohlordnungen)
(m,r) und (m*,r*) seien Wohlordnungen. Dann ist
(m,r) isomorph zu einem Anfangsabschnitt von (m*,r*)
oder es ist (m*,r*) isomorph zu einem Anfangsabschnitt von (m,r).
Beweis:
Seien (m,r) und (m*,r*) Wohlordnungen.
Ist f ein Isomorphismus von irgendeinem Anfangsabschnitt von
(m,r) auf einen der Anfangsabschnitte von (m*,r*), so soll hierfür
f:ISM(m,r;m*,r*)
geschrieben werden. Gemäß POT und AUS existiert die Menge
p = { f∈∈℘(m x m*) | f:ISM(m,r;m*,r*) }.
Sind nun f,g ∈∈ p
mit dom(f) ⊆ dom(g),
so folgt mit W2, dass g|dom(f) = f.
Hiermit hat man f ⊆ g.
Umgekehrt folgt aus dom(g) ⊆ dom(f)
auf entsprechende Weise g ⊆ f.
In jedem Fall gilt also für alle f,g ∈∈ p
f|dom(f) ∩ dom(g) = g|dom(f) ∩ dom(g).
Hieraus folgt, dass h, definiert durch h =def ⋃p, eine Funktion ist; darüberhinaus gilt h ∈∈ p.
Im Falle dass dom(h) = m
(oder rng(h) = m*),
ist mit h (oder mit h−1)
ein Isomorphismus gemäß der Behauptung gefunden worden.
Angenommen, dass
(*) dom(h) ǂ m
und rng(h) ǂ m*.
Sei dann a das r-minimale Element von m\dom(h) und b das r*-minimale Element von m*\rng(h). Dann gilt für herw, definiert durch
herw =def h ∪ { (a; b) },
herw ∈∈ p
und damit auch herw ⊆ h.
Nach Definition gilt aber h ⊂ herw.
Widerspruch!
Der Fall (*) kann also nicht eintreten.
Sei F ein zweistelliger Operator und (m,r) eine fundierte Struktur. Dann nennt man a einen Anfang von (m,r) (oder kurz: einen Anfang) genau dann, wenn
(i) a eine Funktion ist,
(ii) dom(a) ein Anfangsstück von
m bezüglich r ist und
(iii) das Folgende gilt:
∀x (x ∈∈ dom(a) ⇀ a(x) = F(x, a|r[x])).
Ist a ein Anfang einer fundierten Struktur (m,r), so soll hierfür abkürzend „a:ANF(m,r)“ geschrieben werden.
Falls r ǂ ∈∈m,
kann es durchaus vorkommen, dass r[x] = r[y]
für x,y ∈∈ m
mit x ǂ y.
![]() W5
W5
Zwei Anfänge einer fundierten Struktur stimmen auf dem Durchschnitt ihrer Definitionsbereiche überein.
Beweis:
Seien sowohl a als auch b Anfänge einer fundierten Struktur (m,r).
Sei u = { x ∈∈ dom(a) ∩ dom(b) | a(x) ǂ b(x) }.
Angenommen, die Menge u ist nicht leer.
Dann besitzt u ein r-minimales Element, das mit
x* bezeichnet sei. Hiermit gilt a|r[x*] = b|r[x*].
Also folgt
a(x*) = F(x*, a|r[x*]) = F(x*, b|r[x*]) = b(x*).
Widerspruch zu x* ∈∈ u!
Demnach ist u = Ø, was zu beweisen
war.
Es soll nun das Rekursionstheorem für fundierte Strukturen bewiesen werden:
![]() W6 (Rekursionstheorem für fundierte Strukturen)
W6 (Rekursionstheorem für fundierte Strukturen)
Sei F ein zweistelliger Operator und (m,r) eine
fundierte Struktur. Dann existiert genau eine auf m definierte
Funktion f, für die Folgendes gilt:
∀x (x ∈∈ m ⇀ f(x) = F(x, f|r[x]) ).
Beweis:
Sei F ein zweistelliger Operator und (m,r) eine
fundierte Struktur.
d =def { x∈∈m | ∃a (a:ANF(m,r) ˄ x ∈∈ dom(a)) }.
Aus c ∈∈ d folgt, dass es eine Menge a gibt mit
a:ANF(m,r) ˄ c ∈∈ dom(a).
Wegen a:ANF(m,r) ist dom(a)
Anfangsstück von m bezüglich r, also folgt r[c] ⊆ dom(a)
und damit r[c] ⊆ d.
Demnach ist auch d ein Anfangsstück von m bezüglich r.
Sei x ∈∈ d und
a ein Anfang von (m,r) mit
x ∈∈ dom(a).
Dann ist ad(x) =def a(x)
wegen W5 unabhängig von der Wahl von
a und damit bei vorgegebenem x eindeutig bestimmt.
Sei nun der Operator G wie folgt definiert:
G(x) =def ad(x),
falls x ∈∈ d;
Ø, falls x ∉∉ d,
dann ist mit
f =def G|d
eine wie im Satz geforderte Funktion gefunden und wegen W5
eindeutig bestimmt.
Bleibt zu zeigen:
(i) f ist ein Anfang von (m,r).
(ii) m = dom(f).
zu (i):
dom(f) = d. Demzufolge
ist nach dem oben Gesagten f eine Funktion und dom(f)
ein Anfangsstück von m bezüglich r.
Sei x ∈∈ dom(f),
dann gilt
f(x) = ad(x) = F(x, a|r[x]) = F(x, f|r[x]),
wobei
a irgendein Anfang von (m,r) ist mit
x ∈∈ dom(a).
Demnach gilt f(x) = F(x, f|r[x])
für alle x ∈∈ dom(f).
zu (ii):
Angenommen, m\d sei nicht leer.
Dann gibt es ein r-minimales Element m* ∈∈ m\d
und
f ∪ { (m*, F(m*, f|r[m*]) }
ist ein Anfang von (m,r).
Hieraus folgt m* ∈∈ d.
Widerspruch!
Im vorletzten Abschnitt wurde gezeigt, dass man die Elemente jeder endlichen Menge mit Hilfe der natürlichen Zahlen bzw. der vonNeumann’schen Zahlen abzählen kann, anders ausgedrückt: man kann die Elemente einer endlichen Menge m nummerieren: erstes, zweites, drittes Element von m, und so fort. In diesem Abschnitt wird gezeigt, dass es auch möglich ist, die Elemente unendlicher Mengen zu nummerieren, und zwar mit Hilfe der sogenannten Ordinalzahlen.
Gemäß des Vorschlags von Wolfgang Rautenberg (1936−2011) kann eine Ordinalzahl wie folgt definiert werden:
Eine Menge a heißt genau dann Ordinalzahl, wenn a erblich transitiv ist, das heißt, wenn a und jedes Element von a transitiv ist.
Ordinalzahlen sollen im Folgenden - wie allgemein üblich - mit griechischen
Buchstaben und die Klasse aller Ordinalzahlen mit „𝑶“
bezeichnet werden.
Zur Erinnerung:
Eine Menge a heißt transitiv genau dann, wenn das Folgende gilt:
∀x∈∈a (x ⊆ a).
Da alle Elemente von ω transitive Mengen sind (N2) und jedes Element von ω nur Elemente von ω umfasst (N6), folgt sofort, dass alle n ∈∈ ω und ω selbst Ordinalzahlen sind. Die vonNeumann’schen Zahlen sind die einzigen endlichen Ordinalzahlen; ω ist die erste transfinite Ordinalzahl.
![]() O1
O1
Jedes Element einer Ordinalzahl ist ebenfalls eine Ordinalzahl.
Beweis:
Sei α ∈∈ 𝑶 und x ∈∈ α.
Dann ist x auf jeden Fall transitiv.
Außerdem folgt x ⊆ α,
weil α transitiv ist.
Damit hat man mit y ∈∈ x
auch y ∈∈ α, also ist y transitiv.
Demnach sind alle Elemente von x transitiv.
![]() O2
O2
𝑶 ist eine echte Klasse.
Beweis:
Alle Elemente von 𝑶 sind nach Definition transitiv.
Angenommen, 𝑶 ist eine Menge.
Mit ξ ∈∈ 𝑶 gilt nach O1 auch ξ ⊆ 𝑶,
denn 𝑶 umfasst alle Ordinalzahlen.
Also ist auch 𝑶 transitiv und damit eine Ordinalzahl.
Es folgt 𝑶 ∈∈ 𝑶 im Widerspruch zu FND!
Also ist 𝑶 keine Menge.
![]() O3
O3
Sei
α eine Ordinalzahl. Dann ist
s(α), definiert durch s(α) =def α ∪ {
α }, auch eine Ordinalzahl.
Beweis:
Sei α ∈∈ 𝑶 und x ∈∈ s(α).
Dann ist x ∈∈ α ˅
x ∈∈ { α }.
Aus x ∈∈ α
folgt x ⊆ α
wegen α ∈∈ 𝑶. Damit hat man x ⊆ α ∪ {
α }.
Falls x ∈∈ { α },
so folgt x = α
und damit ist ebenso x ⊆ α ∪ {
α }.
Also ist s(α) transitiv.
Ferner sind wegen α ∈∈ 𝑶 auch α
und alle x ∈∈ α transitiv.
Damit sind alle Elemente von s(α) transitiv.
Wegen O3 lässt sich die Zählreihe 0, 1, 2, ..., ω
über ω hinaus fortsetzen. Die Nachfolgermenge von ω ist nach Definition s(ω) = ω ∪ { ω };
danach folgt ω ∪ { ω } ∪ { ω ∪ { ω } },
u.s.w.
Diese hier banal klingende Aussage war zu Cantors Lebzeiten
sensationell und geradezu ungeheuerlich. Er schreibt 1883 in seinen Grundlagen
einer allgemeinen Mannigfaltigkeitslehre im §1:
Die Abhängigkeit, in welche ich mich von dieser Ausdehnung des Zahlbegriffs versetzt sehe, ist eine so große, daß es mir ohne letztere kaum möglich sein würde, zwanglos den kleinsten Schritt weiter vorwärts in der Mengenlehre auszuführen; möge in diesem Umstande eine Rechtfertigung oder, wenn nötig, eine Entschuldigung dafür gefunden werden, daß ich scheinbar fremdartige Ideen in meine Betrachtungen einführe. Denn es handelt sich um eine Erweiterung resp. Fortsetzung der realen ganzen Zahlenreihe über das Unendliche hinaus; so gewagt dies auch scheinen möchte, kann ich dennoch nicht nur die Hoffnung, sondern die feste Überzeugung aussprechen, daß diese Erweiterung mit der Zeit als eine durchaus einfache, angemessene, natürliche wird angesehen werden müssen. Dabei verhehle ich mir keineswegs, daß ich mit diesem Unternehmen in einen gewissen Gegensatz zu weitverbreiteten Anschauungen über das mathematische Unendliche und zu häufig vertretenen Ansichten über das Wesen der Zahlgröße mich stelle.
Man bezeichnet die auf ω folgenden Ordinalzahlen mit ω+1, ω+2, u.s.w., indem rekursiv die folgende Schreibweise vereinbart wird:
α+0 =def α; α+s(n) =def
s(α+n)
für alle α mit α ∈∈ 𝑶.
Also können wir bis jetzt wie folgt zählen:
0, 1, 2, ..., ω, ω+1, ω+2, ...
![]() O4
O4
𝑶 ist mit „∈∈“ partiell geordnet.
Beweis:
Seien α, β und
γ beliebige Ordinalzahlen.
(i) Irreflexivität:
Es gilt stets α ∉∉ α
wegen FND.
(ii) Transitivität:
Jede Ordinalzahl ist eine transitive Menge.
Aus α ∈∈ β ˄ β ∈∈ γ folgt demnach α ∈∈ β ˄ β ⊆ γ,
also gilt auch α ∈∈ γ.
Man schreibt gewöhnlich „β < α“ statt „β ∈∈ α“.
Für "β < α ˅ β = α" schreibt man „β ≤ α“.
![]() O5
O5
Sei m eine nichtleere Menge von Ordinalzahlen. Dann sind ∩m
und ⋃m auch
Ordinalzahlen.
Beweis:
Weil m eine Menge ist, sind auch ∩m
und ⋃m Mengen (siehe oben).
Falls x ∈∈ ∩m,
so gilt x ∈∈ α
für ein beliebiges α ∈∈ m.
Aus α ∈∈ 𝑶 folgt, dass x transitiv ist.
Damit sind alle Elemente von ∩m transitiv.
Aus x ∈∈ ∩m
folgt darüberhinaus x ⊆ α
für alle α ∈∈ m.
Also gilt x ⊆ ∩m,
womit auch ∩m selbst transitiv ist.
Falls x ∈∈ ⋃m,
so gibt es ein αx ∈∈ m
mit x ∈∈ αx.
Wegen αx ∈∈ 𝑶 ist x und
damit jedes Element von ⋃m transitiv.
Für jedes x ∈∈ ⋃m
gilt x ⊆ αx ∈∈ m
und damit auch x ⊆ ⋃m.
Sei φ ein einstelliges Prädikat. Es soll nun bewiesen werden, dass φ auf alle Ordinalzahlen zutrifft, wenn man zeigen kann, dass φ auf eine beliebige Ordinalzahl α zutrifft unter der Voraussetzung, dass φ auf all diejenigen Ordinalzahlen zutrifft, die kleiner als α sind:
![]() O6 (Satz von der transfiniten Induktion für
O6 (Satz von der transfiniten Induktion für 𝑶)
Sei φ ein einstelliges Prädikat und α ∈∈ 𝑶, dann gilt:
∀α (∀β<α
(φ(β) ⇀
φ(α)) ⇀ ∀α (φ(α)).
Beweis:
Voraussetzung: ∀β (β <
α ⇀
φ(β)) ⇀
φ(α) für alle α.
Annahme: Es existiert eine Ordinalzahl δ mit ¬φ(δ).
Man definiere nun die Menge μ derjenigen Elemente von δ+1,
für die φ nicht zutrifft:
μ =def { γ ∈∈ δ+1 | ¬φ(γ) }.
Dann ist μ nicht leer, denn wegen δ ∈∈ δ+1 folgt
δ ∈∈ μ.
Alle Elemente von μ sind wegen O3 und O1
Ordinalzahlen.
Gemäß FND besitzt μ
mindestens ein ∈∈-minimales Element, das heißt:
es gibt ein Element γ* ∈∈ μ, das
kein Element mit μ gemeinsam hat.
Jedes Element von γ* ist wegen O4
auch Element von δ+1.
Also gilt φ(β) für
alle β <
γ*.
Nach Voraussetzung folgt damit φ(γ*). Widerspruch, denn
γ* ∈∈ μ.
Also war die Annahme falsch und es gilt φ(δ) für alle δ, was zu zeigen war.
Aus dem Induktionssatz für 𝑶 folgt der
Satz von der
kleinsten Ordinalzahl:
![]() O7 (Satz von der kleinsten Ordinalzahl)
O7 (Satz von der kleinsten Ordinalzahl)
Jede nichtleere Menge m von Ordinalzahlen besitzt ein kleinstes Element.
Formal geschrieben:
∃α∈∈m (∀β (β <
α ⇀
β ∉∉ m)).
Beweis:
Sei m eine nichtleere Menge von Ordinalzahlen.
Angenommen, m besitzt kein kleinstes Element α, dann folgt
∀α (∀β (β <
α ⇀
β ∉∉ m)) ⇀
α ∉∉ m).
Mit O6 ergibt sich
∀α
(α ∉∉ m).
Daraus folgt m = Ø, ein Widerspruch zur Annahme!
![]() O8
O8
𝑶 ist mit „<“
linear geordnet.
Beweis:
Seien α und β
Ordinalzahlen.
zu zeigen: α ≤ β ˅ β ≤ α (Konnexität).
Angenommen, es gibt eine nichtleere Menge
m = { β | ∄α∈∈𝑶 (α ≤ β ˅ β ≤ α) }
Dann hat wegen O7 m ein kleinstes Element β* und gemäß dieser Annahme ist auch die Menge
m* = { α | ¬(α ≤ β*) ˄ ¬(β* ≤ α) }
nicht leer. Nach O7 hat ebenso m* ein kleinstes Element α*, das heißt:
(*) δ ≤ β* ˅ β* ≤ δ für alle δ < α*.
Sowohl β* ≤ δ ˄ δ < α*
als auch β* = δ
liefert einen Widerspruch zu β* ∈∈ m.
Aus (*) folgt also
(**) δ < α* ⇀ δ < β*,
was gleichbedeutend ist mit δ ∈∈ α* ⇀ δ ∈∈ β*.
Hieraus folgt α* ⊆ β*.
Wegen α* ∈∈ m*
ist α* = β*
ausgeschlossen, also ergibt sich
α* ⊂ β*.
β* ist das kleinste Element von
m, also folgt α* ≤ δ* ˅ δ < α
wegen δ ∈∈ β*
respektive δ < β*.
Mit δ ∈∈ β*\α*
(so ein δ gibt es, denn α* ist
eine
echte Teilmenge von β*)
ergibt sich α* ≤ δ.
Aus α* ≤ δ
und δ < β*
ergibt sich α* < β*
und hieraus mit β* ∈∈ m ein Widerspruch zur Annahme!
Zusammen mit O4 folgt die Behauptung.
Von den Aussagen "α < β",
"β < α" und
"α = β" für zwei beliebig
ausgewählte Ordinalzahlen kann stets nur genau eine Aussage richtig sein: Sowohl "α < β ˄ α = β" als
auch "β < α ˄ α = β" können
nie gelten wegen der Irreflexivität bezüglich „<“. Aus
demselben Grund ist auch "α < β ˄ β < α
immer eine falsche Aussage, denn mit α < β ˄ β < α
würde wegen der Transitivität von „<“ die
falsche Aussage "α ∈∈ α" folgen.
![]() O9
O9
𝑶 ist wohlgeordnet.
Mit 𝑶 ist auch jede nichtleere Menge von Ordinalzahlen wohlgeordnet.
![]() O10
O10
Sei α eine
beliebig gewählte Ordinalzahl. Dann gilt α < s(α)
und es existiert keine Ordinalzahl ξ
mit α < ξ < s(α).
Beweis:
s(α) = α ∪ { α }.
Also folgt aus β ∈∈ s(α),
dass β ∈∈ α ˅ β = α.
Anders ausgedrückt: β < s(α) ⇀ β ≤ α.
Dies ist äquivalent mit α <
β ⇀ s(α) ≤ β.
Hieraus folgt die Behauptung.
s(α) = α ∪ {
α } mit α ∈∈ 𝑶
heißt Nachfolgerzahl (ein Name, der nach O10 gerechtfertigt ist).
Ist eine von 0 verschiedene Ordinalzahl λ keine
Nachfolgerzahl, so ist λ eine Limeszahl.
Die Klasse aller Limeszahlen soll mit „𝑳“ bezeichnet werden.
ω ist die kleinste Limeszahl.
![]() O11
O11
Jede Ordinalzahl α umfasst alle diejenigen Elemente von α, die kleiner sind als α:
α ∈∈ 𝑶 ⇀ α = { ξ ∈∈ s(α) | ξ <
α }.
Beweis:
entspricht dem Beweis von N6.
Die Formulierung "{ ξ ∈∈ s(α) | ξ <
α }" statt "{ ξ | ξ <
α }" ist zwingend im
Hinblick auf AUS und sinnvoll unter
Beachtung von O3, O8 und O10.
O11 besagt insbesondere, dass jede Ordinalzahl α ǂ Ø als nichtleere Menge von Ordinalzahlen wohlgeordnet ist.
![]() O12
O12
Sind zwei Wohlordnungen (α,∈∈α)
und (β,∈∈β)
isomorph zueinander, so gilt α = β.
Beweis:
Sei (α,∈∈α) ≅ (β,∈∈β)
und ohne Beschränkung der Allgemeinheit α ⊆ β.
Dann ist (α,∈∈α)
ein Anfangsabschnitt von (β,∈∈β).
Mit W3 folgt (α,∈∈α) = (β,∈∈β)
und damit α = β.
Aus dem Rekursionstheorem für fundierte Strukturen folgt
der Rekursionssatz für 𝑶, eine
Verallgemeinerung vom Rekursionssatz für ω:
![]() O13 (Rekursionssatz für
O13 (Rekursionssatz für 𝑶)
Sei F ein einstelliger Operator. Dann existiert für jede
Ordinalzahl
μ genau eine auf μ
definierte
Funktion f, für die Folgendes gilt:
∀ξ (ξ < μ ⇀ f(ξ) = F(f|ξ) ).
Beweis:
(μ,r)
mit r = ∈∈μ ist eine Wohlordnung und damit eine
fundierte Struktur.
Sei F* ein zweistelliger Operator. Dann existiert
gemäß W6 genau eine auf μ definierte
Funktion f, für die Folgendes gilt:
(*) ∀ξ (ξ ∈∈ μ ⇀ f(ξ) = F*(ξ, f|r[ξ]) ).
Für alle ξ ∈∈ μ
gilt wegen O11 r[ξ] = ξ.
Damit wird aus (*)
∀ξ (ξ < μ ⇀ f(ξ) = F*(ξ, f|ξ) ).
Der erste Parameter von F* erweist sich hier als überflüssig; es folgt die Behauptung.
![]() O14
O14
Für alle Ordinalzahlen gilt
α <
β ⇌
α ⊂ β.
Beweis:
„⇀“:
Da β als Ordinalzahl gemäß Definition eine transitive Menge ist, folgt aus
α <
β zunächst
α ⊆ β.
Wegen α <
β ist
α ǂ β, also folgt
α ⊂ β.
„↽“:
Sei α ⊂ β.
Angenommen, ¬(α <
β).
Weil 𝑶 linear geordnet ist, folgt β ≤ α
und damit β ⊆ α
wegen der Transitivität von α.
Widerspruch zur Annahme!
Aus O14 folgt sofort, dass auch
α ≤ β ⇌
α ⊆ β
gilt.
![]() O15
O15
Sei m eine nichtleere Menge von Ordinalzahlen. Dann ist ∩m
das kleinste Element von m.
Beweis:
Für alle
α ∈∈ m
gilt ∩m ⊆ α
und demzufolge auch ∩m ≤ α.
Angenommen, ∩m < α für alle
α ∈∈ m,
dann folgt ∩m ∈∈ ∩m.
Widerspruch zu O4(i)!
Es gibt also ein μ ∈∈ m mit ∩m = μ
und damit gilt ∩m ∈∈ m.
Gemäß O9 besitzt m ein kleinstes Element.
Angenommen, es gibt ein κ ∈∈ m mit κ < ∩m.
Dann hat man κ < ∩m < κ
und damit die falsche Aussage κ < κ.
Es folgt die Behauptung.
Sei a mit „<“ partiell geordnet
und b eine nichtleere Teilmenge b ⊆ a.
Dann heißt b nach oben beschränkt, wenn es ein k ∈∈ a gibt mit x ≤ k für alle x ∈∈ b. Ein solches k heißt obere Schranke von b. Existiert für eine nach oben beschränkte Menge b eine obere Schranke k* mit k* ≤ k für alle oberen Schranken k von b, so heißt k* Supremum (oder obere Grenze) von b in a. In Zeichen:
k* = sup b.
b heißt nach unten beschränkt, wenn es ein k ∈∈ a gibt mit x ≥ k für alle x ∈∈ b. Ein solches k heißt untere Schranke von b. Existiert für eine nach unten beschränkte Menge b eine untere Schranke k* mit k* ≥ k für alle unteren Schranken k von b, so heißt k* Infimum (oder untere Grenze) von b in a. In Zeichen:
k* = inf b.
Ist b nach unten und oben beschränkt, so heißt b beschränkt.
![]() O16
O16
Sei m eine nichtleere Menge von Ordinalzahlen. Dann ist m nach
oben beschränkt und ⋃m das
Supremum von m in 𝑶.
Beweis:
Zur Erinnerung: ⋃m = { ξ | ∃α (α ∈∈ m ˄ ξ ∈∈ α) }
und es ist ⋃m ∈∈ 𝑶 wegen O5.
Aus α ∈∈ m
folgt α ⊂ m,
das heißt, ξ ∈∈ ⋃m
für alle ξ ∈∈ α.
Demnach gilt α ⊆ ⋃m und
damit α ≤ ⋃m
für alle α ∈∈ m.
Also ist ⋃m eine obere
Schranke von m.
Sei σ eine weitere obere Schranke von m.
Dann gilt α ≤ σ
bzw. α ⊆ σ
für alle α ∈∈ m.
Es folgt ⋃m ⊆ σ
und demzufolge auch ⋃m ≤ σ,
was zu beweisen war.
Mit O16 und O3 ist bewiesen, dass es zu jeder Menge α von Ordinalzahlen stets eine noch größere gibt: s(sup α) ist größer als jedes Element von α und größer als α.
Man mag sich an dieser Stelle erinnern, wie Cantor 1883 eine wohlgeordnete Menge charakterisiert hat. Er schreibt in seinen Grundlagen einer allgemeinen Mannigfaltigkeitslehre im §2:
Unter einer wohlgeordneten Menge ist jede wohldefinierte Menge zu verstehen, bei welcher die Elemente durch eine bestimmt vorgegebene Sukzession mit einander verbunden sind, welcher gemäß es ein erstes Element der Menge gibt und sowohl auf jedes einzelne Element (falls es nicht das letzte in der Sukzession ist) ein bestimmtes anderes folgt, wie auch zu jeder beliebigen endlichen oder unendlichen Menge von Elementen ein bestimmtes Element gehört, welches das ihnen allen nächst folgende Element in der Sukzession ist (es sei denn, dass es ein ihnen allen in der Sukzession folgendes überhaupt nicht gibt).
Ein echter Anfang μ von 𝑶,
also eine Menge mit β < α ˄ α ∈∈ μ ⇀ β ∈∈ μ
für alle α,β ∈∈ μ,
ist als Teil von 𝑶 auch
wohlgeordnet und lässt sich stets fortsetzen, das heißt: es gibt bei gegebenem μ
immer eine nächste
Ordinalzahl ν. Hat μ
ein Maximum τ, dann gilt ν = s(τ)
(ν ist dann eine Nachfolgerzahl),
andernfalls setzt man ν = sup μ
(dann ist ν eine Limeszahl).
![]() O17
O17
Sei φ ein einstelliges Prädikat. Gilt (i) φ(0),
(ii) φ(α) ⇀ φ(s(α))
für alle Ordinalzahlen α und
(iii) ∀β (β < λ ⇀ φ(β)) ⇀ φ(λ)
für alle Limeszahlen λ,
so gilt φ(α)
für alle Ordinalzahlen α.
Beweis:
Angenommen, es gibt ein α*, für
das φ(α*) nicht
gilt. Wegen O7 darf angenommen
werden, dass α* die kleinste
Ordinalzahl ist mit ¬φ(α*).
Wegen (i) ist α* ǂ 0; wegen (ii) ist α* keine Nachfolgerzahl und wegen (iii) keine Limeszahl. Widerspruch zur Annahme!
Mal angenommen, man hätte für irgendeine Menge ein geeignetes Verfahren gefunden, um die Elemente dieser Menge unter Verwendung der Ordinalzahlen wiederholungsfrei abzuzählen: m0, m1, m2, m3, ... Dann ist aufgrund des eben Gesagten nicht zu erwarten, dass diese Abzählung irgendwann einmal abbrechen könnte, etwa weil zum Weiterzählen nicht genügend viele Ordinalzahlen zur Verfügung stehen. Dieser Erwartung entsprechend gilt der nach Friedrich Moritz Hartogs (1874−1943) benannte Satz von Hartogs:
![]() O18 (Satz von Hartogs)
O18 (Satz von Hartogs)
Für alle Mengen m gibt es eine Ordinalzahl ξ,
für die keine Injektion von ξ
nach m existiert; als Formel geschrieben:
∀m ∃ξ (∄f ( f: ξ inj→ m )).
Beweis:
Angenommen, die behauptete Formel ist keine wahre Aussage, dann gilt
(*)
∃m ∀ξ (∃f ( f: ξ inj→ m )).
Sei m eine Menge, für die die Aussage (*) zutrifft
und sei ξ beliebig, aber fest gewählt.
Das kartesische Produkt zweier Mengen ist stets eine Menge; die Potenzmenge
einer Menge ist ebenfalls eine Menge, also existiert gemäß AUS
w = { (m; r) ∈∈ ℘(m)x℘(mxm) | (m,r) ∈∈ 𝑾 }.
Die Menge w repräsentiert alle Wohlordnungen, deren Trägermenge eine Teilmenge von m ist.
Sei nun f die zu m und ξ
gemäß (*) existierende Funktion mit f: ξ inj→ m.
Dann ist (ξ,∈∈ξ) ≅ (rng(f),t)
mit
t =def { (f(α); f(β)) ∈∈ mxm | α,β ∈∈ ξ ˄ α < β }.
und es gilt (rng(f),t) ∈∈ w. Somit hat man
(**) Für jedes ξ
gibt es ein xξ ∈∈ w mit
xξ ≅ (ξ,∈∈ξ).
Falls zu einem x ∈∈ w
eine Ordinalzahl ζ mit x ≅ (ζ,∈∈ζ) existieren sollte, so ist dieses ζ
gemäß O12 eindeutig bestimmt und soll mit ζx bezeichnet
werden. Sei nun der Operator F definiert durch
F(x) =def ζx,
falls x∈∈w ˄ ∃ζ (x ≅ (ζ,∈∈ζ)); Ø sonst.
Mit ERS folgt, dass F|w
eine Menge ist; wegen (**) ist F|w
die Menge aller Ordinalzahlen. Dies ist ein Widerspruch zu O2.
Demnach ist die anfangs angenommene Formel (*) falsch, was zu zeigen war.
![]() O19
O19
Sei w eine Wohlordnung. Dann gibt es genau eine Ordinalzahl ξ
mit (ξ,∈∈ξ) ≅ w.
Beweis:
Sei w = (m,r) eine
Wohlordnung. Dann sei ξ gemäß O18
so gewählt, dass es keine Injektion von ξ
nach m gibt. Wegen W4 ist (i) (m,r)
isomorph zu einem Anfangsabschnitt von (ξ,∈∈ξ)
oder (ii) (ξ,∈∈ξ)
ist isomorph zu einem Anfangsabschnitt von (m,r). Da eine
Injektion von ξ nach m nicht existiert, folgt (i). Demnach gibt es ein μ
mit μ ≤ ξ und der Eigenschaft, dass
(μ,∈∈μ) ≅ (m,r).
Dieses μ ist wegen O12 eindeutig bestimmt.
![]() O20
O20
Eine Menge m ist genau dann zu einer Ordinalzahl gleichmächtig,
wenn es eine Relation r gibt,
so dass (m,r)
eine Wohlordnung ist.
Beweis:
„⇀“:
Sei f: μ ∼ m.
Dann gilt mit
r =def { (f(α); f(β)) ∈∈ mxm | α,β ∈∈ μ ˄ α < β }
f: (μ,∈∈μ) ≅ (m,r)
und - da (μ,∈∈μ) ∈∈ 𝑾
- gilt auch (m,r) ∈∈ 𝑾.
„↽“:
Sei (m,r) ∈∈ 𝑾. Dann folgt aus O19 (m,r) ≅ (μ,∈∈μ)
und somit m ∼ μ mit
einer eindeutig bestimmten Ordinalzahl μ.
O20 ist der letzte der Bausteine, die nötig sind, um den von Cantor 1883 formulierten und von Zermelo 1904 erstmalig bewiesenen Wohlordnungssatz zu beweisen:
![]() O21 (Wohlordnungssatz)
O21 (Wohlordnungssatz)
Für jede Menge m gibt es eine Relation r auf m,
so dass m mit r wohlgeordnet ist.
Beweis:
Sei m eine nichtleere, aber ansonsten beliebig gewählte Menge.
Wegen O20 genügt es zu zeigen, dass
eine Ordinalzahl existiert, die zu m gleichmächtig ist.
Gemäß R3 gibt es eine
Auswahlfunktion f auf ℘(m).
Es gilt f(u) ∈∈ m
für alle u ∈∈ ℘(m)
mit u ǂ Ø.
f(Ø) soll kein Element von m sein.
Nach dem Satz von Hartogs gibt es eine
Ordinalzahl μ, für die keine
Injektion von μ nach m
existiert. Aus dem Rekursionssatz für 𝑶
folgt, dass es genau eine auf μ
definierte rekursive Funktion g gibt mit
(*) g(ξ) =def f(m\rng(g|ξ))
für alle ξ ∈∈ μ.
rng(g|0) = Ø,
also ist g(0) = f(m); g(1) = f(m\{ g(0) }); g(2) = f(m\{ g(0), g(1) });
und so weiter. Mit anderen Worten: Im ersten Schritt wird ein Element
aus m ausgewählt, welches nach Definition als Bild von 0
unter g genommen wird; im zweiten Schritt wird ein Element aus der
Restmenge m\{ g(0) } ausgewählt und als Bild
von 1 unter g genommen; und so weiter. Die Menge m\rng(g|ξ)
umfasst also - sofern sie nicht leer ist - nach jedem Schritt die jeweils
noch nicht ausgewählten Elemente von m. Im Falle, dass schließlich m\rng(g|ξ) = Ø,
gilt g(ξ) = f(Ø).
Aufgrund der Eigenschaften von f gilt für den Wertebereich von g
(**) rng(g) ⊆ m ∪ {
f(Ø) }.
Man kann nun das Folgende zeigen:
(***) ∀ξ≤μ (f(Ø) ∉∉ rng(g|ξ) ⇀ g|ξ : ξ inj→ m):
Sei f(Ø) ∉∉ rng(g|ξ)
und α,β ∈∈ ξ
mit α ǂ β.
Sei ohne Beschränkung der Allgemeinheit α < β.
Es folgt mit (**), dass rng(g|β) ⊂ m.
Wegen (*) hat man g(β) ∉∉ rng(g|β)
und damit g(β) ǂ g(α),
was zu zeigen war.
Es gibt ein ξ < μ
mit g(ξ) = f(Ø),
denn gäbe es ein solches ξ nicht,
so wäre f(Ø) ∉∉ rng(g)
und gemäß (***)
g: μ inj→ m,
ein Widerspruch, denn μ wurde anfangs so gewählt, dass keine Injektion von μ nach m existiert.
Da es ein ξ < μ
mit g(ξ) = f(Ø)
gibt, ist die Menge
p =def { ξ < μ | g(ξ) = f(Ø) }
nicht leer. Nach O7 besitzt p
ein kleinstes Element, etwa γ.
Daraus folgt g|γ: γ inj→ m
wegen (***). Weil g(γ) = f(Ø)
hat man wegen (**) rng(g|γ) = m,
das heißt: g|γ: γ sur→ m
und somit ergibt sich
γ ∼ m.
Es folgt die möglicherweise sehr irritierende Tatsache, dass zum Beispiel auch ℝ, die Menge der reellen Zahlen, wohlgeordnet werden kann! Der Beweis des Wohlordnungssatzes liefert allerdings keinerlei Informationen darüber, mit welcher Relation ℝ wohlgeordnet werden bzw. auf welche Weise man eine solche Relation konstruieren könnte.
Die vonNeumann’sche Hierarchie
![]()
In Übereinstimmung mit der Definition eines Anfangs einer fundierten Struktur wird Folgendes festgelegt:
Sei F ein einstelliger Operator, μ
eine Ordinalzahl und a eine Funktion auf μ. Dann nennt man a einen Anfang
von
𝑶 (oder kurz: einen Anfang) genau
dann, wenn
∀ξ (ξ ∈∈ μ ⇀ a(ξ) = F(a|ξ)).
Ist a ein Anfang von
𝑶, so soll hierfür abkürzend „a:ANF“ geschrieben werden.
![]() H1
H1
Sei F ein einstelliger Operator. Dann gibt es einen Operator G mit
(*)
G(m) = F(G|m),
falls m ∈∈ 𝑶; Ø sonst
und dieser ist mit (*) eindeutig festgelegt.
Beweis:
Sei F ein einstelliger Operator.
(i) zu zeigen: Es gibt nur ein G mit (*).
Angenommen, es gibt zwei Operatoren G und G*, die der
Bedingung (*)
genügen.
Falls m keine Ordinalzahl ist, folgt G(m) = G*(m) = Ø.
Sei nun α eine beliebige
Ordinalzahl.
Vorausgesetzt, dass G(β) = G*(β)
für alle β < α,
so folgt G|α = G*|α
und hieraus ergibt sich
G(α) = F(G|α) = F(G*|α) = G*(α).
Wegen O6 folgt G(α) = G*(α)
für alle α.
(ii) zu zeigen: G, definiert durch
G(x) =def a(x), falls a:ANF ˄ x∈∈𝑶 ˄ x∈∈dom(a);
Ø sonst
erfüllt die Bedingung (*).
Sei ξ eine Ordinalzahl, a ein
Anfang und ξ ∈∈ dom(a).
Dann gilt
G(ξ) = a(ξ) = F(a|ξ) = F(G|ξ),
was zu zeigen war.
(iii) zu zeigen: G ist
wohldefiniert.
Der Rekursionssatz für 𝑶 garantiert, dass
es für jede Ordinalzahl ξ einen
Anfang a gibt mit dom(a) = ξ.
Darüberhinaus stimmen nach W5
jeweils zwei Anfänge auf dem Durchschnitt ihrer Definitionsbereiche
überein, was bedeutet, dass a(ξ)
gemäß obiger Definition in jedem Fall eindeutig bestimmt ist.
Sei der Operator FV definiert durch
FV(x) =def
|

|
℘(x(α)),falls x ∈∈ 𝑭 ˄ dom(x) = s(α)
mit α∈∈𝑶 |
⋃{ x(β) | β < λ }falls x ∈∈ 𝑭 ˄ dom(x) = λ
mit λ∈∈𝑳 |
||
| Ø sonst, |
dann hat man mit H1 den eindeutig bestimmten Operator V mit
V(m) =
|

|
℘(V(mp))
mit m =
s(mp),falls m eine Nachfolgerzahl ist |
⋃{ (V(β) | β < m }falls m eine Limeszahl ist |
||
| Ø sonst, |
unter Beachtung der Tatsache, dass eine Ordinalzahl entweder gleich 0 oder eine Nachfolgerzahl oder eine Limeszahl ist.
Üblicherweise werden die Argumente von V als Indizes geschrieben, und zwar wie folgt:
V0 =
|
Ø |
Vs(α) =
|
℘(Vα) |
Vλ =
|
⋃{ Vβ | β < λ } |
Vm =
|
𝑶) |
Auf genau die gleiche Art wird weiter unten der Aleph-Operator ℵ definiert.
![]() H2
H2
Vμ ist eine transitive
Menge für jede Ordinalzahl μ.
Beweis:
zu zeigen: ∀x∈∈Vμ (x ⊆ Vμ).
(i) Für μ = 0
ist dies trivialerweise wahr.
(ii) Angenommen, Vμ
ist für irgendein μ transitiv.
Sei nun m ∈∈ Vs(μ).
Dann folgt m ⊆ Vμ
nach Definition von Vs(μ).
Mit x ∈∈ m
gilt demnach x ∈∈ Vμ,
also auch x ⊆ Vμ
nach Annahme.
Damit hat man x ∈∈ Vs(μ),
und zwar für alle x ∈∈ m.
Hieraus folgt m ⊆ Vs(μ)
und damit ist auch Vs(μ)
transitiv.
(iii) Die Vereinigung transitiver Mengen ist wieder transitiv, also ist Vμ
nach Definition auch dann transitiv, wenn μ
eine Limeszahl ist.
Mit O17 folgt die Behauptung.
![]() H3
H3
Für beliebige Ordinalzahlen α
und β
gilt
(*) β < α ⇀ Vβ ∈∈ Vα
(**) β ≤ α ⇀ Vβ ⊆ Vα
Beweis:
Sei die Ordinalzahl β beliebig,
aber fest gewählt.
(i) Für α = 0
gilt
(*) trivialerweise.
(ii) Angenommen,
(*) gilt für irgendein α.
Dann folgt aus β < s(α),
dass β ≤ α,
also Vβ ∈∈ Vα
oder Vβ = Vα.
Mit H2 hat man somit Vβ ⊆ Vα.
Es ist also Vβ ∈∈ ℘(Vα) = Vs(α)
und damit gilt (*) auch für s(α).
(iii) Sei nun λ eine beliebige
Limeszahl
und es gelte (*) für alle α < λ.
Mit α < λ
ist
auch s(α) < λ,
also gilt β < s(α) ⇀ Vβ ∈∈ Vs(α) ⊆ Vλ.
Wegen O17 gilt (*)
also für alle α.
(**) folgt mit H2
aus (*).
Sei nun
𝑽 =def [
x | ∃α∈∈𝑶 (
x ∈∈ Vα)
]
die Klasse all derjenigen Mengen, die Element einer vonNeumann’schen Stufe Vα sind und m eine zu 𝑽
gehörende Menge. Dann gibt es eine Ordinalzahl μ
mit m ∈∈ Vμ
und gemäß AUS die Menge vm =def { β < s(μ) | m ∈∈ Vβ }. vm
ist wegen μ ∈∈ vm
nicht leer, also besitzt nach O7 vm
ein kleinstes Element, etwa σm.
Aufgrund der Definition des Operators V muss σm
zwangsläufig eine Nachfolgerzahl sein, das heißt, es gilt σm = s(ρm)
mit ρm als Vorgänger
von σm.
Somit ist ρm
eindeutig bestimmt. Da für m lediglich die Zugehörigkeit zu 𝑽
vorausgesetzt wurde, gibt es ein derartiges ρm
für alle m ∈∈ 𝑽,
so dass die folgende Definition sinnvoll ist:
![]() H4
H4
Für alle Ordinalzahlen α gilt α ∈∈ 𝑽
und
rg(α) = α.
Beweis:
Sei α ∈∈ 𝑶.
Dann folgt α ⊆ Vα mit O17 und H2.
Es ist also α ∈∈ Vs(α)
und damit auch α ∈∈ 𝑽.
Aus α ∈∈ Vs(α)
folgt außerdem rg(α) ≤ α.
zu zeigen: α ∉∉ Vβ
für alle β ≤ α.
Wegen H3(**)
genügt es, α ∉∉ Vα
zu zeigen:
(i) α ∉∉ V0,
denn V0 = Ø.
(ii) Es gelte α ∉∉ Vα
für ein beliebiges α.
Angenommen, s(α) ∈∈ Vs(α),
dann folgt
α ∪ { α } ⊆ Vα, also
α ∈∈ Vα.
Widerspruch!
Es ist also s(α) ∉∉ Vs(α).
(iii) Sei nun λ ∈∈ 𝑳
und β ∉∉ Vβ
für alle β < λ.
Angenommen, λ ∈∈ Vλ,
dann gibt es
mindestens ein β < λ
mit λ ∈∈ Vβ.
Also gilt λ ⊆ Vβ
wegen H2 und damit β ∈∈ Vβ.
Widerspruch! Es gilt also λ ∉∉ Vλ.
![]() H5
H5
Für alle x,y ∈∈ 𝑽
gilt
x ∈∈ y ⇀ rg(x) < rg(y).
Beweis:
y ∈∈ 𝑽
bedeutet, dass y ∈∈ Vs(rg(y))
bzw. y ⊆ Vrg(y)).
Mit x ∈∈ y
hat man auch x ∈∈ Vrg(y)).
Hieraus folgt die Behauptung.
![]() H6
H6
Es gilt
x ∈∈ 𝑽 ⇌ x ⊆ 𝑽.
Beweis:
„⇀“:
Aus x ∈∈ 𝑽
folgt x ∈∈ Vs(rg(x))
und mit H2 hat man x ⊆ Vs(rg(x)),
also auch x ⊆ 𝑽
gemäß Definition von 𝑽.
„↽“:
Sei x ⊆ 𝑽
vorausgesetzt. Mit
β =def ⋃{ μ ≤ rg(x) | μ = s(rg(y))
mit y ∈∈ x }
hat man x ⊆ Vβ.
Hieraus folgt x ∈∈ Vs(β)
und somit x ∈∈ 𝑽.
Die Klasse 𝑽
ist nach den vorstehenden Ergebnissen kumulativ-hierarchisch aufgebaut. Es beginnt mit der
leeren Menge und gemäß H3 umfasst
dann jedes Vs(μ) alle
vorherigen Vβ:
V0 = Ø
V1 = { Ø }
V2 = { Ø, { Ø } }
V3 = { Ø, { Ø }, { { Ø } }, { Ø, { Ø } } }
u.s.f.
Jede zu 𝑽
gehörende nichtleere Menge m erscheint hierbei erstmalig als Teilmenge
der rg(m)-ten Stufe, um dann den jeweils darauffolgenden
Stufen als Element anzugehören. Umgekehrt umfasst jede Stufe Vs(μ)
alle Mengen m mit rg(m) ≤ μ;
insbesondere ist μ ∈∈ Vs(μ)
für alle μ ∈∈ 𝑶. So
gilt zum Beispiel für die Elemente von
V3:
rg({ Ø, { Ø } }) = rg(2)
= 2,
rg({ { Ø } }) = 2,
rg({ Ø }) = rg(1)
= 1,
rg(Ø) = rg(0)
= 0.
Die Anzahl N(μ) der Elemente in den vonNeumann’schen Stufen Vμ wächst mit zunehmendem μ stark an und wird sehr schnell unvorstellbar groß:
| μ | N(μ) |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 16 |
| 5 | 65536 |
| 6 | 265536 |
| ... | ... |
![]() H7
H7
Zu jeder Menge m gibt es eine transitive Obermenge und
darüberhinaus eine kleinste transitive Obermenge. (Die somit
eindeutig bestimmte kleinste transitive Obermenge von m heißt
transitive Hülle von m.)
Beweis:
Die Menge m sei beliebig gewählt.
(i) zu zeigen: ∃v (m ⊆ v).
Sei hierzu gemäß N9 f
rekursiv auf ω definiert durch
f(0) =
m
f(s(n)) = ⋃f(n)
für alle n ∈∈ ω.
Dann ist mit v =def ⋃rng(f)
eine Obermenge von m gefunden.
(ii) zu zeigen: v ist eine transitive Menge.
Sei x ∈∈ v,
dann gibt es ein n* ∈∈ ω,
so dass x ∈∈ f(n*).
Nach Definition von f folgt x ⊆ f(s(n*))
und damit x ⊆ v, was zu
zeigen war.
(iii) Sei nun w eine transitive Obermenge von m.
Dann lässt sich mit dem Induktionssatz für ω
nachweisen, dass v ⊆ w.
zu zeigen: f(n) ⊆ w
für alle n ∈∈ ω.
f(0) ⊆ w gilt nach Voraussetzung.
Angenommen, es gilt f(n) ⊆ w
für irgendein n ∈∈ ω.
Dann gilt für jedes x ∈∈ f(n)
auch x ∈∈ w
und damit x ⊆ w.
Für alle e ∈∈ x
folgt demnach e ∈∈ w.
Dies bedeutet ⋃f(n) ⊆ w
und somit
f(s(n)) ⊆ w.
Somit ist ⋃rng(f)
die transitive Hülle von m.
![]() H8
H8
Sei φ(m) ein einstelliges Prädikat. Wenn es eine Menge m gibt, auf die dieses Prädikat zutrifft, dann gilt
∃m (φ(m) ˄ ∀x (x ∈∈ m ⇀
¬φ(x)))
Beweis:
Sei erstens m eine Menge, für die
φ(m) zutrifft.
Sei zweitens die Funktion f auf ω
wie folgt definiert:
f(0) = {
m }
f(s(n)) = ⋃f(n)
für alle n ∈∈ ω.
f ist nach Z6 und VER
wohldefiniert. v, definiert durch v =def ⋃rng(f),
ist nach H7
eine transitive Obermenge von m.
Sei nun
w =def {
u ∈∈ v
|
φ(u) }.
Nach Definition von f ist m ∈∈ v,
also ist w nicht leer. Das Fundierungsaxiom garantiert, dass
w ein ∈∈-minimales Element
besitzt, etwa u*. Es gilt
φ(u*). Wenn x ∈∈ u*,
so
folgt x ∈∈ v,
denn mit u* ∈∈ v
hat man auch u* ⊆ v,
weil v transitiv ist. Aus x ∈∈ v ˄ x ∈∈ u*
folgt x ∉∉ w
und damit
¬φ(x).
![]() H9
H9
Zu jeder Menge m gibt es ein μ,
so dass m ∈∈ Vμ,
mit anderen Worten:
𝑩 = 𝑽.
Beweis:
Angenommen, es gibt eine Menge, die nicht zu 𝑽
gehört. Dann gibt es nach H8 eine
Menge m mit m ∉∉ 𝑽
so dass x ∈∈ 𝑽
für alle x ∈∈ m.
Hieraus folgt aber m ⊆ 𝑽
und damit gilt nach H6 auch m ∈∈ 𝑽.
Widerspruch!
Cantor beginnt seinen Beitrag zur Mannigfaltigkeitslehre 1878 mit den Worten „Wenn zwei wohldefinirte Mannigfaltigkeiten M und N sich eindeutig und vollständig, Element für Element, einander zuordnen lassen (was, wenn es auf eine Art möglich ist, immer auch noch auf viele andere Weisen geschehen kann), so möge für das folgende die Ausdrucksweise gestattet sein, dass diese Mannigfaltigkeiten gleiche Mächtigkeit haben, oder auch, dass sie äquivalent sind.“ In heutiger Sprache bedeutet das: Für zwei Mengen a und b gilt a ∼ b genau dann, wenn eine Funktion f existiert, so dass f: a bij→ b (a und b heißen dann äquivalent oder gleichmächtig).
Gemäß dieser Definition ist das Prädikat ∼ offensichtlich reflexiv, symmetrisch und transitiv. ∼ hat also formal die gleichen Eigenschaften wie eine Äquivalenzrelation.
Seien a und b Mengen. Dann heißt a höchstens so mächtig wie b (kurz formuliert: „a ≼ b“) genau dann, wenn
∃f (f: a inj→ b).
Gilt a ≼ b und ¬(a ∼ b), so soll „a ≺ b“ geschrieben werden (gesprochen: „b ist mächtiger als a“).
Aus der Definition von ≼ folgt wegen ida: a inj→ b sofort, dass
a ⊆ b ⇀ a ≼ b.
Aufgrund von O14 bedeutet dies für Ordinalzahlen α und β:
α ≤ β ⇀
α ≼ β.
Die Implikationen a ⊂ b ⇀ a ≺ b
bzw. α < β ⇀ α ≺ β sind
im Allgemeinen nicht gültig! Man betrachte zum Beispiel eine Ordinalzahl α
mit
ω ≤ α.
Dann gilt
α < s(α) wegen O11,
aber es ist α ∼ s(α),
denn s ∪ id|α\ω ∪ { (α; 0) } ist
eine Bijektion von s(α) auf
α.
Seien α und β voneinander verschiedene Ordinalzahlen. Gibt es dann eine Injektion von α nach β, so folgt, dass α eine Teilmenge von β sein muss, das heißt:
α ≺ β ⇀ α < β.
Hieraus folgt zusammen mit E9
∀m,n∈∈ω
(m ≺ n ⇌ m < n).
![]() M1
M1
Wenn a ∼ a*
und b ∼ b*
gilt, so folgt
(i)
a ≼ b ⇌ a* ≼ b*
(ii) a ≺ b ⇌ a* ≺ b*.
Beweis:
Sei f: a bij→ a*
und g: b bij→ b*.
Wenn h: a inj→ b,
so ist die Komposition g∘h∘f−1
eine Injektion von a* nach b*.
Aus h*: a* inj→ b*
folgt, dass g−1∘h∘f eine
Injektion von a nach b ist.
Damit gilt (i); (ii) folgt umittelbar.
![]() M2
M2
Für alle Mengen a, b und c gilt
(i)
a ≼ a
(ii) a ≼ b ˄ b ≼ c ⇀ a ≼ c
(iii) a ≼ b ˅ b ≼ a.
Beweis:
Die Aussagen (i) und (ii) sind ohne Weiteres klar.
(iii) Für alle α,β ∈∈ 𝑶
gilt
(*) α ≼ β ˅ β ≼ α,
denn Ordinalzahlen sind nach O8
vergleichbar: α ⊆ β ˅ β ⊆ α.
Seien nun a und b irgendwelche Mengen.
Dann gibt es gemäß O20 und O21 α,β ∈∈ 𝑶
mit a ∼ α und
b ∼ β.
Mit (*) folgt die Behauptung.
![]() M3
M3
Ist a eine Teilmenge von b und b höchstens so mächtig wie a, dann sind a und b äquivalent:
a ⊆ b ˄ b ≼ a ⇀ a ∼ b.
Beweis:
Seien a und b zwei Mengen mit
a ⊆ b ˄ b ≼ a.
Aus b ≼ a
folgt die Existenz einer Funktion f mit f: b inj→ a.
Also ist b ∼ rng(f)
mit rng(f) ⊆ a.
Wenn u eine Teilmenge von b ist, so sei u* =def rng(f|u).
Sei ferner q =def
b \ a. Dann existiert gemäß AUS
die Menge
t =def
{ u ∈∈ ℘(b) | q ⊆ u ˄ u* ⊆ u }.
Wegen q ⊆ b und b* ⊆ a ⊆ b ist
b ∈∈ t,
also ist t nicht leer. Somit ist auch
d =def
∩t
nicht leer. q ist Teilmenge von jedem Element von t,
also hat man q ⊆ d.
Zusammen mit d* ⊆ d folgt
(*)
d ∈∈ t.
Darüberhinaus gilt für alle u ∈∈ ℘(b)
(**)
q ⊆ u ⊆ d ˄ u* ⊆ u ⇀
u = d,
denn gäbe es ein u' ∈∈ t
mit q ⊆ u' ⊂ d, so
würde ein x ∈∈ d mit x ∉∉ u'
existieren,
was aber im Widerspruch dazu steht, dass nach Definition jedes
Element von d auch Element von jedem u' ∈∈ t
ist.
Wegen (*) und (**) ist d
bezüglich ⊆ die kleinste Teilmenge von
b, welche q umfasst und bezüglich f abgeschlossen ist.
Aus f: b inj→ a
und d* ⊆ d folgt,
dass f|d eine Injektion von d nach (a ∩ d)
ist. Andererseits ist f|d auch eine Surjektion von d
auf (a ∩ d),
also hat man insgesamt
d ∼ a ∩ d.
zu zeigen: rng(f|d) = a ∩ d.
Angenommen, es gibt ein x ∈∈ (a ∩ d) \ rng(f|d).
Dann gilt mit dx =def d \ { x }
q ⊆ dx ⊆ d ˄ dx* ⊆ dx.
Wegen (**)
folgt dx = d und damit ein Widerspruch, was zu zeigen war.
Mit f|d: d ∼ (a ∩ d)
folgt
f|d ∪ id|a\d:
b ∼ a.
![]() M4 (Äquivalenzsatz)
M4 (Äquivalenzsatz)
Für alle Mengen a und b gilt
a ≼ b ˄ b ≼ a ⇀ a ∼ b.
Beweis:
Sei f: b inj→ a
und g: a inj→ b.
Dann ist rng(g) ⊆ b
und g∘f: b inj→ rng(g).
Mit M3 hat man rng(g) ∼ b
und wegen g: a inj→ b
gilt a ∼ rng(g).
Es folgt die Behauptung.
Die Beweise von M3 und M4 orientieren sich an der Argumentation von Ebbinghaus (Einführung in die Mengenlehre, Kapitel IX, Satz 1.4(iii). Die zugrunde liegende Beweisidee geht zurück auf Zermelo, der den Äquivalenzsatz 1907 bewies (Untersuchungen über die Grundlagen der Mengenlehre. I., Nr. 25 und Nr. 27). In der Fußnote zu den Nrn. 25 und 27 schrieb Zermelo, dass der von ihm gegebene Beweis „im Gegensatz zu den älteren Beweisen von E. Schröder und F. Bernstein, sowie zu dem letzten Beweise von J. König ... jede Bezugnahme auf geordnete Reihen vom Typus ω oder das Prinzip der vollständigen Induktion“ vermeidet. Das Gleiche gilt für die Beweise von M3 und M4. (Der von Cantor 1883 formulierte Äquivalenzsatz wurde zuerst von Dedekind bewiesen: der Satz mit vollständigem Beweis wurde erst nach seinem Tod in seinem Tagebuch von 1887 gefunden.)
![]() M5 (Satz von Cantor)
M5 (Satz von Cantor)
Die Potenzmenge einer Menge m ist stets mächtiger als m:
∀m (m ≺ ℘(m)).
Beweis:
Sei m beliebig gewählt. Dann ist
f =def
{ (x; y) ∈∈ m x ℘(m) | y = { x } }
insbesondere wegen Z6 eine Funktion. Aus { x } ǂ { y } folgt stets x ǂ y, also ist f darüberhinaus eine Injektion, und es gilt demnach
(*)
m ≼ ℘(m).
Angenommen, es gibt eine Funktion g von m auf ℘(m),
das heißt g: m sur→ ℘(m).
Dann ist
v =def
{ x ∈∈ m | x ∉∉ g(x) }
als Teilmenge von m Element von rng(g) und für das
Urbild u von v gilt u ∈∈ m
und v = g(u). Die
Definition von v liefert hiermit einen Widerspruch: u ∈∈ v ⇌ u ∉∉ v.
Damit ist gezeigt, dass m nicht äquivalent zu ℘(m)
ist, also folgt mit (*) die Behauptung.
![]() M6
M6
Zu jeder Ordinalzahl α gibt es eine
Ordinalzahl, die mächtiger ist als α:
∀α∈∈𝑶 ∃β∈∈𝑶 (α ≺ β).
Beweis:
Sei α ∈∈ 𝑶 beliebig
gewählt.
Der Satz von Hartogs besagt,
dass es eine Ordinalzahl β
gibt mit ¬(β ≼ α).
Mit M2(iii) folgt
α ≺ β
und damit die Behauptung.
Mit M6 und O7 folgt die Existenz und die Eindeutigkeit der kleinsten Ordinalzahl κ, welche mächtiger ist als eine beliebig vorgegebene Ordinalzahl α:
κ = min { β∈∈𝑶 | α ≺ β }.
Daher kann nun der Aleph-Operator ℵ definiert werden, und zwar auf die gleiche Art, in welcher oben der Operator V definiert wurde:
ℵ0 =
|
ω |
ℵs(α) =
|
min { β∈∈𝑶 | ℵα ≺ β } |
ℵλ =
|
⋃{ ℵβ | β < λ } |
ℵm =
|
𝑶) |
Jede endliche Menge ist äquivalent zu einer der vonNeumann’schen Zahlen 0, 1, 2, ... (→ Mächtigkeit endlicher Mengen). Es wird sich herausstellen, dass jede unendliche Menge zu einem der Alephs ℵ0, ℵ1, ℵ2, ... äquivalent ist.
Aufgrund der Definition von ℵ sind
alle Alephs Ordinalzahlen und es ist ℵα ≺ ℵs(α),
also gilt auch ℵα < ℵs(α).
Für jedes β mit
ℵα ≤ β < ℵs(α)
folgt β ∼ ℵα,
denn mit β < ℵs(α)
hat man β ≼ ℵs(α)
und da β ∼ ℵs(α) wegen der Definition von ℵs(α)
ausgeschlossen ist, ergibt sich β ≺ ℵs(α).
Alle Ordinalzahlen, die zu einer Zahlklasse
Zα =def [ β∈∈𝑶 | ℵα ≤ β < ℵs(α) ]
gehören, sind also einander äquivalent. ℵα ist die kleinste Ordinalzahl in Zα und heißt deswegen Anfangszahl von Zα. Desweiteren nennt man ω erste Zahlklasse, Z0 zweite Zahlklasse, Z1 dritte Zahlklasse, usf.
![]() M7
M7
Alle Alephs sind Limeszahlen:
∀α∈∈𝑶
(ℵα ∈∈ 𝑳).
Beweis:
(i) ℵ0 = ω ∈∈ 𝑳.
(ii) Sei α beliebig gewählt
und β ∈∈ Zα.
Dann gilt
β ≺ ℵs(α)
und wegen β ∼ s(β)
auch s(β) ≺ ℵs(α),
also s(β) < ℵs(α).
ℵs(α)
ist somit keine Nachfolgerzahl, also eine Limeszahl.
(iii) ℵλ = ⋃{ ℵβ | β < λ } =
sup{ ℵβ | β < λ } wegen O16.
Das Supremum einer Menge von Limeszahlen ist stets eine Limeszahl.
Mit O17 folgt die Behauptung.
![]() M8
M8
Für α,β ∈∈ 𝑶
gilt
(*)
α < β ⇀
ℵα ≺ ℵβ.
Beweis:
Sei die Ordinalzahl α
beliebig, aber fest gewählt.
(i) Für β = 0 gilt (*)
trivialerweise.
(ii) Angenommen, (*)
gilt für β.
Aus α < s(β)
folgt α ≤ β
und gemäß (*) damit auch ℵα ≼ ℵβ.
Mit ℵβ ≺ ℵs(β)
und M2(ii) hat man ℵα ≺ ℵs(β).
(iii) Sei λ eine Limeszahl und (*)
gültig für alle β < λ.
Mit α < λ
ist auch s(α) < λ,
also gilt ℵα ≺ ℵs(α).
Gemäß Definition von ℵλ
ist ℵs(α) ≤ ℵλ.
Hierdurch folgt ℵs(α) ≼ ℵλ
und schließlich ℵα ≺ ℵλ
.
Mit O17 folgt die Behauptung.
![]() M9
M9
Für α,β ∈∈ 𝑶
sind die folgenden Aussagen äquivalent:
(i) α < β
(ii) ℵα ≺ ℵβ.
(iii) ℵα < ℵβ.
Beweis:
(i) ⇀ (ii) wurde mit M8
bewiesen.
(ii) ⇀ (iii) folgt ohne
Weiteres (siehe oben).
noch zu
zeigen: (iii) ⇀ (i).
Sei ¬(α < β),
das heißt β ≤ α.
Falls β =
α, folgt ℵβ
=
ℵα,
mit β < α
folgt ℵβ < ℵα.
In jedem Fall gilt also ¬(α < β) ⇀ ¬(ℵα < ℵβ).
Ein einstelliger Operator ℱ heißt genau dann normal,
wenn er jede Ordinalzahl auf eine Ordinalzahl abbildet, wenn er auf 𝑶
streng
monoton und wenn er auf 𝑳 stetig ist, das heißt, wenn Folgendes
gilt:
∀α∈∈𝑶
(ℱ (α) ∈∈ 𝑶)∀α,β∈∈𝑶
(α < β ⇀ ℱ (α) < ℱ (β))
∀λ∈∈𝑳 (ℱ (λ)
=
⋃{ ℱ (α) | α < λ }).
Aufgrund von M9 und der Definition von ℵλ ist ℵ ein normaler Operator.
![]() M10
M10
Sei ℱ ein normaler Operator und m eine nichtleere Menge von Ordinalzahlen. Dann gilt
ℱ (⋃m)
= ⋃{ ℱ (α) | α ∈∈ m }.
Beweis:
Fall 1: m hat ein größtes Element, etwa μ.
ℱ ist als normaler Operator auf 𝑶
streng monoton und es gilt O11.
Damit hat man
⋃{ ℱ (α) | α ∈∈ m }
= ⋃{ ℱ (α) | α ∈∈ m ˄ α ∈∈ s(μ) }
= ℱ (μ)
= ℱ (⋃m).
Fall 2: m hat kein größtes Element, dann ist
⋃m eine Limeszahl,
etwa λ, und es folgt
ℱ (λ)
=
⋃{ ℱ (α) | α ∈∈ λ }
=
⋃{ ℱ (α) | α ∈∈ m }.
![]() M11
M11
Sei ℱ ein normaler Operator. Dann gilt für alle α ∈∈ 𝑶:
(*)
α ≤ ℱ (α).
(**) ∃β∈∈𝑶 (α ≤ β ˄ ℱ (β)
= β).
Beweis:
(i) 0 ist die kleinste Ordinalzahl, also gilt 0 ≤ ℱ (0).
(ii) Sei (*)
für ein beliebiges α gültig.
Dann folgt α ≤ ℱ (α) < ℱ (s(α))
und damit s(α) ≤ ℱ (s(α))
wegen O10.
(iii) Sei λ
eine Limeszahl und β ≤ ℱ (β)
für alle β < λ.
Dann gilt
λ
= ⋃{ β | β ∈∈ λ }
≤ ⋃{ ℱ (β) |
β ∈∈ λ }
= ℱ (λ).
Mit O17 folgt die Gültigkeit von (*)
für alle α ∈∈ 𝑶.
Sei α ∈∈ 𝑶
beliebig vorgegeben. Dann gibt es gemäß N9 genau eine auf
ω definierte Funktion f mit
f(Ø) = α
∀n∈∈ω (f(s(n)) =
ℱ(f(n))).
Für alle n ∈∈ ω gilt
f(n) ≤ f(s(n)), also hat man α ≤ ⋃rng(f).
Mit M10 folgt
ℱ(⋃rng(f))
= ⋃{ ℱ (β) | β ∈∈ ⋃rng(f) }
= ⋃{ ℱ (f(n)) | n ∈∈ ω }
= ⋃{ f(s(n) | n ∈∈ ω }
= ⋃rng(f).
![]() M12
M12
Sei ℱ ein normaler Operator und
α eine Ordinalzahl mit ℱ (0) ≤ α.
Dann existiert ein größtes β
mit ℱ (β) ≤ α.
Beweis:
Sei α eine Ordinalzahl mit ℱ (0) ≤ α.
ℱ ist als normaler Operator auf 𝑶
streng monoton und es ist α < s(α).
Mit M11(*)
folgt α ≤ ℱ (α) < ℱ (β).
Damit ist die Menge { β | α < ℱ (β) } nicht
leer und hat nach O7 ein kleinstes
Element, genannt β*.
Wegen ℱ (0) ≤ α
ist β* ǂ 0.
Angenommen, β* ist eine
Limeszahl.
Dann folgt ℱ (γ) ≤ α
für alle γ < β*.
Also gilt auch
ℱ (β*)
=< β* }
≤ α
im Widerspruch zu α < ℱ (β*).
β* ist demnach also eine Nachfolgerzahl.
Sei β* = s(δ),
dann ist ℱ (δ) ≤ α
und δ ist maximal mit dieser Eigenschaft.
![]() M13
M13
Zu jeder Ordinalzahl
α mit
ω ≤ α
gibt es genau ein β mit α ∼ ℵβ
und ℵβ ≤ α.
Beweis:
Sei α ∈∈ 𝑶
mit ω ≤ α.
Dann hat nach M12 die Menge { δ < s(α) | ℵδ ≤ α }
ein größtes Element, genannt β.
Für dieses β gilt ℵβ ≤ α < ℵs(β).
Mit M9 folgt unter Beachtung der
Definition von ℵs(β)
α ∼ ℵβ
und die Eindeutigkeit von β.
Eine Ordinalzahl κ
heißt genau dann Kardinalzahl, wenn κ ∈∈ ω
oder wenn es eine Ordinalzahl β
gibt mit κ = ℵβ.
𝑲, die Klasse der Kardinalzahlen, besteht also
aus den vonNeumann’schen Zahlen und allen Alephs.
![]() M14
M14
Zu jeder Menge m existiert eine eindeutig bestimmte Kardinalzahl mit
m ∼ κ:
∀m ∃!κ∈∈𝑲
(m ∼ κ ).
Beweis:
Zu jeder endlichen Menge a existiert nach E7
eine Bijektion f: n bij→ a mit n ∈∈ ω.
Nach E8 ist dieses n eindeutig
bestimmt.
Zu jeder unendlichen Menge u gibt es nach O19, O20
und O21 eine eindeutig bestimmte
Ordinalzahl mit u ∼ α.
Diesem α ist nach M13 eindeutig
eine Ordinalzahl β zugeordnet mit α ∼ ℵβ.
Also folgt u ∼ ℵβ.
Auf Grundlage von M14 kann nunmehr die Mächtigkeit einer Menge definiert werden:
Sei m eine beliebige Menge und κx diejenige Kardinalzahl mit m ∼ κx. Dann heißt
|m| =def κx
Mächtigkeit von m.
Ist |m| ≤ ℵ0 ,so nennt man m abzählbar; wenn ℵ1 ≤ |m|, so heißt m überabzählbar.
Jede endliche Menge ist abzählbar; ω ist abzählbar unendlich; ℘(ω)
ist nach dem Satz von Cantor überabzählbar. ℵ1
ist die kleinste überabzählbare Ordinalzahl.
Für alle Kardinalzahlen κ gilt
|κ| = κ.
Ferner gilt für alle Mengen a und b
a ∼ b ⇌ |a| = |b|
a ≼ b ⇌ |a| ≤ |b|
a ≺ b ⇌ |a| < |b|.
Im Kapitel Zahlen wird detailliert beschrieben, wie nacheinander ℕ zu ℤ, ℤ zu ℚ und ℚ zu ℝ erweitert werden kann. Die Gesamtheit aller ganzen Zahlen, die Gesamtheit aller rationalen Zahlen und die Gesamtheit aller reellen Zahlen können auf der Grundlage von ω unter Verwendung der mengentheoretischen Definition des kartesischen Produkts und unter Beachtung des Auswahlaxioms auch durch Mengen im Sinne von ZFC repräsentiert werden. Denn bezeichnet man die zu einer Äquivalenzrelation r auf einer Menge v gehörende Quotientenmenge wie üblich mit „v/r“, dann kann
ℤ = ℕxℕ/r
alias ℤ = ωxω/r
mit
(n; m) r (n*; m*)
⇌ m + n* = n + m*
für (n; m) (n*; m*) ∈∈ ℕxℕ;
ℚ = ℤx(ℤ\{ 0 })/s mit
(a; b) s (a*; b*)
⇌ a · b* = b · a*
für (a; b),(a*; b*) ∈∈ ℤx(ℤ\{ 0 });
ℝ = fC/t
mit
(xn) t (yn)
⇌ (xn − yn) ist eine Nullfolge
für (xn),(yn) ∈∈ fC
gesetzt werden, wobei fC die Menge aller rationalen Cauchyfolgen
darstellt. Es ist möglich, auf ℤ, ℚ
bzw. ℝ jeweils eine additive Verknüpfung „+“ als
auch eine multiplikative Verknüpfung „·“ so zu definieren, dass
ℕ in ℤ, ℤ in
ℚ, sowie ℚ in
ℝ eingebettet werden können. Es existieren also
Monomorphismen von
ℕ nach ℤ, ℤ
nach ℚ bzw. ℚ
nach ℝ, mit anderen Worten: es gilt
ℕ ∼ ℕ' ⊆ ℤ, ℤ ∼ ℤ' ⊆ ℚ, ℚ ∼ ℚ' ⊆ ℝ
und damit ℕ ≼ ℤ ,
ℤ ≼ ℚ und
ℚ ≼ ℝ.
Sei die Funktion f von ℚ nach ℕ (ab jetzt verlaufen die Argumentationen außerhalb von ZFC!) wie folgt definiert:
g (±zn) =def 2s·pz·qn
für teilerfremde natürliche Zahlen z und n mit n ǂ 0. Es soll s = 1 im Fall „+zn“ und s = 0 im Fall „−zn“ gelten; p und q sind Primzahlen mit p ǂ q und p,q ǂ 2. Dann ist f injektiv, also gilt ℚ ≼ ℕ. Zusammen mit ℕ ≼ ℚ folgt hieraus nach dem Äquivalenzsatz |ℕ| = |ℚ| und damit
|ℕ| = |ℤ| = |ℚ| = ω.
![]() M15
M15
Es gilt
|ℕxℕ| = |ℕ|.
Beweis:
Man belege im ℕxℕ-Gitterdiagramm
das Feld (0; 0) mit der Zahl 0 und das Feld (0; 1) mit der Zahl 1.
Sei das Feld (0; n) bereits mit der Zahl zn belegt, dann sei
(*)
zn+1 =def zn + n+1
für alle n ∈∈ ℕ.
Die (n+1)-te Diagonale hat in jedem Fall nach Belegung des Feldes
(0; n+1) noch n leere Felder. Werden diese Felder nacheinander mit zn+1+1,
zn+1+2, u.s.w. belegt, dann befindet sich im letzten Feld (n+1; 0) die Zahl zn+1 + n+1.
Der Nachfolger dieser Zahl ist aufgrund von (*)
stets gleich zn+2, nämlich gleich zn+2n+3. Diese Argumentation ist unabhängig davon, wie groß n gewählt wird. Das bedeutet, dass die
vollständige Belegung des nach rechts und nach oben offenen Gitterdiagramms eine bijektive Funktion p von ℕxℕ
auf ℕ repräsentiert, die Cantor’sche Paarungsfunktion.
Sei n ∈∈ ℕ beliebig gewählt. Dann gilt für alle Felder (i; j) der n-ten Diagonale im obigen Gitterdiagramm i+j = n. Damit hat man p(i; j) = p(0; n)+ i. Wegen
p(0; n) = n∑j = 0j = n(n+1)2
folgt
p(i; j) = (i+j)(i+j+1)2 + i.
Mit M15 hat man beispielsweise auch |ℤxℤ| = |ℤ| und |ℚxℚ| = |ℚ|, denn die Elemente jeder abzählbaren Menge a lassen sich mit Hilfe der natürlichen Zahlen nummerieren: a0, a1, a2, ... Man beweist dann |axa| = |a| auf die gleiche Weise wie M15. Statt i wird ai und statt j wird aj genommen und man setzt z0 = a0 sowie z1 = a1.
Welche Aussagen sind nun möglich im Hinblick auf die Menge der
reellen Zahlen? Auf jeden Fall gilt ℵ0 < |ℝ|
bzw. ℕ ≺ ℝ,
denn ℝ ist überabzählbar.
![]() M16
M16
Sei (u, v) ein offenes Intervall in ℝ, dann gilt
|(u, v)| = |ℝ|.
Beweis:
Zwei voneinander verschiedene offene Intervalle (u, v) und (s, t) lassen sich immer bijektiv aufeinander abbilden, denn mit
f(x) =def s + x−uv−u·(t−s) für alle x ∈∈ (u, v)
gilt f: (u, v) bij→ (s, t). Es genügt also, die Äquivalenz zwischen ℝ und irgendeinem offenen Intervall zu zeigen. Man nehme hierfür beispielsweise die Tangensfunktion:
tan: (−π2, π2) bij→ ℝ.
![]() M17
M17
Es gilt
|ℝxℝ| = |ℝ|.
Beweis:
Die Funktion f von ℝ nach ℝxℝ,
definiert durch f(x) =def (x; 0),
ist injektiv. Es gilt also ℝ ≼ ℝxℝ.
zu zeigen: ℝxℝ ≼ ℝ.
Wegen |ℤxℤ| = |ℤ|
existiert eine bijektive Funktion g von ℤxℤ
auf ℤ mit g(0; 0) = 0.
Ist (x; y) ∈∈ ℝxℝ,
so kann man x und y in zwei nicht abbrechende Dezimalbrüche
entwickeln (beispielsweise wird 0,29999... statt 0,3 oder 0,0000... statt 0 geschrieben). Es ist also
x = a,d1d2d3d4....
y = b,p1p2p3p4....
Die Vorkommastellen von x bzw. y werden hierbei durch die ganzen Zahlen a bzw. b repräsentiert. Man definiere nun die Funktion h von ℝxℝ nach ℝ nach einer Idee von Cantor wie folgt:
h(x; y) =def g(a; b),d1p1d2p2....
h ist offensichtlich injektiv, was zu zeigen war.
Sei m eine Menge und u ⊆ m.
Dann nennt man die Funktion indu,m
von m nach { 0, 1 } mit
indu,m(x) =
|

|
1, falls x ∈∈ u, |
| 0, falls x ∉∉ u. |
die Indikatorfunktion von u in m.
![]() M18
M18
Sei m eine Menge. Dann ist die Potenzmenge von m äquivalent
zur Menge aller Funktionen von m nach { 0, 1 }.
℘(m) ∼ m{ 0, 1 }.
Beweis:
Die Funktion f von ℘(m)
nach m{ 0, 1 } mit
f(u) =
indu,m für alle u ⊆ m
ist eine Bijektion.
![]() M19
M19
Sei ℘∞(ℕ)
die Menge aller unendlichen Teilmengen von ℕ.
Dann gilt
℘∞(ℕ) ∼ ℘(ℕ).
Beweis:
Wegen ℘∞(ℕ) ⊆ ℘(ℕ)
gilt ℘∞(ℕ) ≼ ℘(ℕ).
Sei ℕa =def { 2n ∈∈ ℕ | n ∈∈ a }
für alle a ⊆ ℕ
und ℕu
die Menge aller ungeraden natürlichen Zahlen.
Die Funktion f von ℘(ℕ)
nach ℘∞(ℕ)
mit
f(a) = ℕa ∪ ℕu
für alle a ⊆ ℕ
ist eine Injektion, also gilt ℘(ℕ) ≼ ℘∞(ℕ).
Mit dem Äquivalenzsatz folgt die Behauptung.
![]() M20
M20
Es gilt
ℝ ∼ ℘(ℕ).
Beweis:
Wegen M16 hat man ℝ ∼ (0, 1)
und somit genügt es wegen ℘∞(ℕ) ∼ ℘(ℕ)
lediglich (0, 1) ∼ ℘∞(ℕ) zu zeigen.
Sei x ∈∈ (0, 1). Dann lässt sich x in einen nicht abbrechenden Dualbruch entwickeln, das heißt:
x = 0,b1b2b3.... mit bn ∈∈ { 0, 1 }.
Die Funktion f von (0, 1) nach ℘∞(ℕ)
mit
f(x) = { n ∈∈ ℕ | bn = 1 }
ist eine Bijektion, was zu zeigen war.
1877 stellte sich Cantor die Frage (Ein Beitrag zur Mannigfaltigkeitslehre, §8), „wie sich die verschiedenen Theile einer stetigen geraden Linie, d. h. die verschiedenen in ihr denkbaren unendlichen Mannigfaltigkeiten von Punkten hinsichtlich ihrer Mächtigkeiten verhalten“ und er schreibt weiter:
Entkleiden wir dieses Problem seines geometrischen Gewandes und
verstehen ... unter einer linearen Mannigfaltigkeit reeller Zahlen
jeden denkbaren Inbegriff unendlich vieler, von einander verschiedener
reeller Zahlen, so fragt es sich in wie viel und in welche Klassen
die linearen Mannigfaltigkeiten zerfallen, wenn Mannigfaltigkeiten von
gleicher Mächtigkeit in eine und dieselbe Klasse, Mannigfaltigkeiten von
verschiedener Mächtigkeit in verschiedene Klassen gebracht werden.
Durch ein Inductionsverfahren, auf dessen Darstellung wir hier nicht näher
eingehen, wird der Satz nahe gebracht, dass die Anzahl der nach diesem
Eintheilungsprincip sich ergebenden Klassen linearer Mannigfaltigkeiten
eine endliche und zwar, dass sie gleich zwei ist.
Darnach würden die
linearen Mannigfaltigkeiten aus zwei Klassen bestehen, von denen die erste
alle Mannigfaltigkeiten in sich fasst, welche sich auf die Form: functio
ips. ν (wo ν alle positiven ganzen Zahlen durchläuft) bringen lassen;
während die zweite Klasse alle diejenigen Mannigfaltigkeiten in sich
aufnimmt, welche auf die Form: functio ips. x (wo x alle reellen Werthe ≥0 und ≤1 aufnehmen kann) zurückführbar sind.
Cantor vermutete also, dass für alle unendlichen Mengen x
mit x ⊆ ℝ
entweder x ∼ ω oder x ∼ ℝ
folgt, mit anderen Worten:
(CH) |ℝ| = ℵ1.
Cantor hat über viele Jahre vergeblich versucht, seine
Kontinuumshypothese zu beweisen. Er musste an dieser Aufgabe
scheitern, denn Kurt Gödel konnte 1938 zeigen, dass die
Kontinuumshypothese nicht widerlegbar ist; Paul Cohen hat
1963 nachgewiesen, dass die Kontinuumshypothese nicht
beweisbar ist. Die Kontinuumshypothese ist also eine von ZFC unabhängige
Aussage. Falls ZFC widerspruchsfrei sein sollte (was nach dem
Zweiten Unvollständigkeitssatz von Gödel grundsätzlich nicht
beweisbar ist), dann ist sowohl ZFC mit (CH), als
auch ZFC mit ¬(CH) widerspruchsfrei. Es ist
demnach innerhalb von ZFC nicht entscheidbar,
ob |ℝ| = ℵ1
oder aber ℵ1 < |ℝ|
gilt: ZFC ist eine unvollständige Theorie (was sich nach dem Ersten Unvollständigkeitssatz von Gödel prinzipiell nicht vermeiden
lässt).
Literatur- und Quellenangaben:
Galileo Galilei:
Unterredungen und mathematische Demonstrationen über zwei neue
Wissenszweige, die Mechanik und die Fallgesetze betreffend, Erster bis
Sechster Tag Arcetri, 6. März 1638
Wissenschaftliche Buchgesellschaft 1973
Georg Cantor:
Ein Beitrag zur Mannigfaltigkeitslehre, 1877
Journal für die reine und angewandte Mathematik 84. Band, S. 242−258
Richard Dedekind:
Was sind und was sollen die Zahlen?
Friedrich Vieweg Verlag, 1887
Georg Cantor:
Grundlagen einer allgemeinen Mannigfaltigkeitslehre. Ein
mathematisch-philosophischer Versuch in der Lehre des Unendlichen.
Teubner Verlag, Leipzig,1883
Georg Cantor:
Beiträge zur Begründung der transfiniten Mengenlehre, 1895
Mathematische Annalen 46. Band, S. 481–493
Ernst Zermelo:
Untersuchungen über die Grundlagen der Mengenlehre. I, 1908
Mathematische Annalen 65. Band, S. 261–281
Kazimierz Kuratowski:
Sur la notion de l’ordre dans la théorie des ensembles, 1921
Fundamenta Mathematicae Volume 2, S. 161–171
A. Fraenkel:
Zu den
Grundlagen der Cantor-Zermeloschen Mengenlehre, 1922
Mathematische Annalen 86. Band, S. 230−237
A. Fraenkel:
Axiomatische Begründung der transfiniten Kardinalzahlen. I., 1922
Mathematische Zeitschrift 13, S. 153−188
A. Fraenkel:
Einleitung in die Mengenlehre, 1928
Die Grundlehren der mathematischen
Wissenschaften, Band IX
John von Neumann:
Über die Definition durch transfinite Induktion und verwandte Fragen der
allgemeinen Mengenlehre, 1928
Mathematische Annalen 99. Band, S. 373–391
Heinz-Dieter Ebbinghaus:
Einführung in die Mengenlehre
Spektrum Akademischer Verlag, 4. Auflage 2003
Wolfgang Rautenberg:
Grundkurs Mengenlehre
Vorlesungsskript 2008
Oliver Deiser:
Einführung in die Mengenlehre
www.aleph1.info 2018
Chris Preston:
Finite Sets and Counting
https://arxiv.org/abs/0809.0105v2 2010
