dh-Materialien
Maple   Übersicht
 

Operatoren
(Auswahl)

 Binäre Operatoren    Unäre Operatoren    Funktionsoperatoren    Differentialoperator    Elementweise Operatoren 

Binäre Operatoren

Binäre Operatoren (binary operators) verknüpfen zwei Operanden miteinander.

+ Rechenzeichen plus
  b + b;
2 b
− Rechenzeichen minus
  5 - 6;
−1
* "mal"
  a*a;
a2
/ "geteilt durch"
  3./4;
0.75000 
^ "potenziert mit"
  2^10;
1024
mod "modulo"
  8 mod 3;
2
 
< "kleiner als"
  x < y;
x < y
<= "kleiner als oder  gleich"
  x <= y;
x ≤  y
> "größer als"
  x > y;
 x > y
>= "größer als oder gleich"
  x >= y;
x ≥  y
= "gleich"
  a = b;
a = b
<> "ungleich"
  3 <> 5;
3 ≠ 5
 
:= Zuweisungsoperator
  v:= lambda*f;
$ Folgenoperator
  x$3;
x, x, x
@ Verkettungsoperator
  f@g;  
f@g
|| Verbindungsoperator
  i:= 8: f||i;
f8
, Trennungsoperator
  m, n;
m, n
   
union Vereinigung von Mengen 
  r,s,t} union {s,t,u}; 
{r, s, t, u}
intersect   Schnitt von Mengen
  {a,b} intersect {b,c};
{b}
minus Differenz von Mengen
  {a,b} minus {b,c};
{a}
   
subset "Teilmenge von?"
  {a,b} subset {a,b,c};
true
and logisches und
  3>0 and 3<0;
false
or logisches oder
  3>0 or 3<0;
true
xor logisches exklusiv-oder
  3>0 xor 3>0
false
implies   "impliziert"
  false implies true;
true
   
:: Typoperator
  k::even;
k::even
assuming "angenommen, dass"
  y:= sin(k*Pi/2):
y assuming k::even;
0

Differenzieren

Der links-assoziative Punktoperator (dot operator) hat - je nach Kontext - unterschiedliche Bedeutungen.
Es folgen ein paar Beispiele:

> v:= Vector([a[1], a[2]]);
  w:= Vector([b[1], b[2]]):
  A:= Matrix([[a[11], a[12]], [a[21], a[22]]]);
  B:= Matrix([[b[11], b[12]], [b[21], b[22]]]): ;
 
  ’6 . 7’ = 6 . 7;
  ’v . w’ = v . w;
  ’7 . A’ = 7 . A;
  ’A . B’ = A . B;

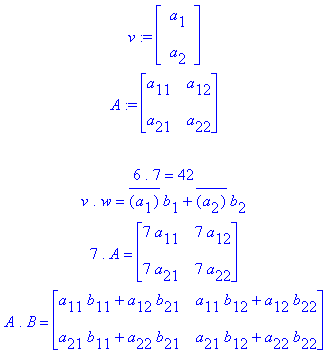
Beispiele für den Punktoperator

 

Unäre Operatoren

Unäre Operatoren (unary operators) haben nur einen Operanden.

 +   Vorzeichen plus  +5;    5
 −   Vorzeichen minus   -a;   −a
 !  "Fakultät"  4!;    24
 not   logisches nicht  not p;    not p  
 .   Dezimalpunkt  .36;    0.36



Funktionsoperatoren

Mit Funktionsoperatoren (functional operators) werden in Maple Funktionen dargestellt.

Ein Funktionsoperator "Variable(n) -> Ergebnis"  beschreibt eine Prozedur, die auf eine Folge von Werten (bzw. auf einen Wert) angewandt wird. Das Rechenergebnis dieser Prozedur wird durch den Ausdruck hinter dem Zuordnungsoperator "->" festgelegt.

Beispiele:
> (x -> x^2)(3);
      9
> ((x, y) -> x + y)(2, 5);
      7

Alternativ zum Zuordnungsoperator kann auch die Funktion unapply verwendet werden. Die folgenden zwei Eingaben liefern dasselbe Resultat:
> f:= x -> x^2;
  
> f:= unapply(x^2, x);
    

Wenn der Ausdruck hinter dem Zuordnungsoperator ein algebraischer Ausdruck ist (das heißt ein Ausdruck, der nur mit Hilfe der arithmetischen Operatoren +, -, *, / und ^ gebildet wird), dann kann der Funktionsterm f(x) der durch eine solche Zuordnungsvorschrift definierten Funktion f auf einfache Art ausgewertet werden.

Beispiele:

> f:= x -> x^2;
  f(4);
   

> f:= x -> (3*x - x^2)/(1 - x);
  f(12);
 

> f:= x -> sum(i^2, i = 1..x);
  f(10);
  

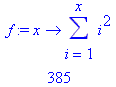
Wenn der Ausdruck hinter dem Zuordnungsoperator kein algebraischer Ausdruck ist, dann gelingt die Auswertung von Funktionstermen auf folgende Art.

Beispiele:

> f:= x -> sqrt(x);
  f(5);
  evalf(f(5));
 

> f:= x -> sin(x)^2*cos(x);
  f(Pi/4);
  evalf(f(Pi/4));
 

Bei miteinander verketteten Funktionen sieht das Ganze wie folgt aus:

> f:= x -> x^2;
  g:= x -> sin(x);
  h:= f@g;
  h(5);
  evalf(h(5));
 

Weitere Beispiele von Funktionsoperatoren:

> f:= x -> sin(x):
  f(Pi/4);
  

> (f1 + f2)(x);
      f1(x) + f2(x)

> ((x -> sqrt(x+1))@@2)(x);
  


Differentialoperator

Der Differentialoperator D (differential operator) wird angewandt auf Funktionen.
D(f) ist die Ableitungsfunktion von f.

> D(sin);
     cos

> D(ln);
  

> D(x -> x^2);
   

Differenzieren


Elementweise Operatoren

Ab Maple 13 besteht die Möglichkeit, Operatoren auf die Elemente von Listen, Mengen, Arrays, Matrizen oder Vektoren wirken zu lassen (element-wise operations). Man schreibt hierfür eine Tilde direkt nach dem jeweiligen Operatorzeichen bzw. nach dem Funktionsnamen.
Beispiele:

> [2, 4, 3] *~ [3, 2, 5];
  [false, true, false] implies~ [true, false, false];
  {3, 4, 5} +~ 1;

[6, 8, 15]
[true, false, true]
{4, 5, 6}