Die Bolzanofunktion
> restart; with(plots): with(plottools):
Definition zweier Startpunkte A und B:
> A:= [2, 3];
B:= [10, 11];
![]()
Konstruktionsvorschrift nach Bolzano:
> newPoints:= proc(A, B)
local a, b, alpha, beta,
d, e, delta, epsilon,
C, D, E;
a:= A[1]: alpha:= A[2]:
b:= B[1]: beta:= B[2]:
C:= [(a + b)/2, (alpha + beta)/2]:
d:= a + 3/8*(b - a):
delta:= alpha + 5/8*(beta - alpha):
e:= a + 7/8*(b - a):
epsilon:= beta + 1/8*(beta - alpha):
D:= [d, delta]:
E:= [e, epsilon]:
RETURN ([A, D, C, E, B]):
end:
d, e, delta, epsilon,
C, D, E;
a:= A[1]: alpha:= A[2]:
b:= B[1]: beta:= B[2]:
C:= [(a + b)/2, (alpha + beta)/2]:
d:= a + 3/8*(b - a):
delta:= alpha + 5/8*(beta - alpha):
e:= a + 7/8*(b - a):
epsilon:= beta + 1/8*(beta - alpha):
D:= [d, delta]:
E:= [e, epsilon]:
RETURN ([A, D, C, E, B]):
end:
Algorithmus für den jeweils nächsten Iterationsschritt:
> nextStep:= proc(plist)
local i, plen, len, newlist;
plen:= nops(plist);
newlist:= []:
for i from 1 to plen-1 do
newlist:= [op(newlist), op(newPoints(plist[i], plist[i+1]))];
len:= nops(newlist):
newlist:= subsop(len=NULL, newlist);
od;
newlist:= [op(newlist), plist[plen]];
RETURN (newlist):
end:
plen:= nops(plist);
newlist:= []:
for i from 1 to plen-1 do
newlist:= [op(newlist), op(newPoints(plist[i], plist[i+1]))];
len:= nops(newlist):
newlist:= subsop(len=NULL, newlist);
od;
newlist:= [op(newlist), plist[plen]];
RETURN (newlist):
end:
Bolzano-Iteration in n Schritten:
> bolzano:= proc(A, B, n)
local i, plist;
plist:= [A, B]:
for i from 1 to n do
plist:= nextStep(plist):
od:
RETURN (plist):
end:
plist:= [A, B]:
for i from 1 to n do
plist:= nextStep(plist):
od:
RETURN (plist):
end:
Der erste Iterationsschritt:
> B||0:= bolzano(A, B, 0);
B||1:= bolzano(A, B, 1);
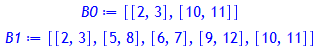
Approximation der Bolzanofunktion:
> opts:= color = navy,
axesfont = [COURIER, 12],
size = [400, 300]:
axesfont = [COURIER, 12],
size = [400, 300]:
graph:= curve(bolzano(A, B, 7)):
display(graph, opts);
display(graph, opts);