Lösen linearer Gleichungssysteme
> restart;
Lösen eines linearen Gleichungssystems mit 3 Gleichungen und 4 Variablen
![]()
gl3:= gl(2, -5, -5, 8, 3):
gl1; gl2; gl3;
![]()
![]()
![]()
> x[3]:= t;
![]()
![]()
![]()
![]()
Lösen eines 3x3-Gleichungssystems mit Hilfe von LinearSolve
> restart; with(LinearAlgebra):
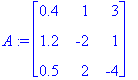
![b:= [2, 3, 1/2]](images-llinglsy/llinglsy31.gif)
A und b definieren ein lineares 3x3-Gleichungssystem mit den Unbekannten x1, x2 und x3:
> ls:= Multiply(A, <x[1], x[2], x[3]>):
for i to 3 do ls[i] = b[i] od;
![]()
![]()
![]()
Lösen dieses Gleichungssystems, d.h. Lösen der Gleichung A x = b:
od;
![]()
![]()
![]()
Die allgemeine Lösung eines 3x3-Gleichungssystems
> restart; with(LinearAlgebra):
[a[31], a[32], a[33]]]);
B:= <b[1], b[2], b[3]>;

![B = [b1, b2, b3]](images-llinglsy/llinglsy30.gif)

> Determinant(A);
![]()
Die Gleichung Ax = B ist also nur dann eindeutig lösbar, wenn die Determinante von A von 0 verschieden ist.
