Lösungen einer Pell’schen Gleichung
> restart; with(numtheory):
Wahl einer beliebigen nicht-quadratischen natürlichen Zahl:
> d:= 57;
Die zu d gehörende Pell’sche Gleichung x2 − d·y2 = 1:
> pell:= x^2 - d*y^2 = 1:
pell;
Berechnen von cf, dem Kettenbruch von
:
> cf:= cfrac(sqrt(d), 'periodic', 'quotients'):
sqrt(d) = cf;
len:= nops(op(cf)[2]): # Periodenlänge
cfrac(sqrt(d), 2*len + 1);
len:= nops(op(cf)[2]): # Periodenlänge
cfrac(sqrt(d), 2*len + 1);
![sqrt(57) = [[7],[1,1,4,1,1,14]]](images-pell/pell3.gif){kind=small}
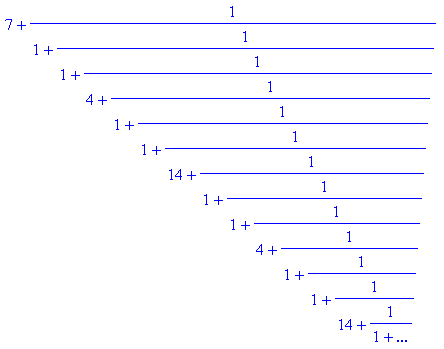
Die Näherungsbrüche für
bis zur 15. Ordnung:
> konv:= NULL:
for i from 1 to 15 do
konv:= konv, nthconver(cf, i);
od:
konv;
konv:= konv, nthconver(cf, i);
od:
konv;
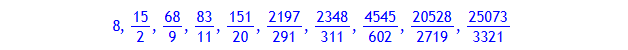
Der n1-te Näherungsbruch ist der erste, der eine nicht-triviale Lösung für die Gleichung pell liefert:
> if is(len, even) then
n[1]:= len - 1;
l:= len:
fi;
if is(len, odd) then
n[1]:= 2*len - 1;
l:= 2*len:
fi;
l:= len:
fi;
if is(len, odd) then
n[1]:= 2*len - 1;
l:= 2*len:
fi;
![n[1]:= 5; l:= 6](images-pell/pell6.gif)
Berechnung der n1-ten Konvergenten des Kettenbruchs von
:
> nthconver(cf, n[1]);
x:= nthnumer(cf, n[1]);
y:= nthdenom(cf, n[1]);
x^2 - d*y^2;
y:= nthdenom(cf, n[1]);
x^2 - d*y^2;
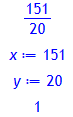
Auflistung weiterer Lösungen der Gleichung x2 − d·y2 = 1:
> for i from 0 to 5 do
x:= nthnumer(cf, n[1]+i*l):
y:= nthdenom(cf, n[1]+i*l):
lsg[i]:= [x, y]:
od:
for i from 0 to 5 do
lsg[i];
lsg[i][1]^2 - d*lsg[i][2]^2;
od;
y:= nthdenom(cf, n[1]+i*l):
lsg[i]:= [x, y]:
od:
for i from 0 to 5 do
lsg[i];
lsg[i][1]^2 - d*lsg[i][2]^2;
od;
![[151, 20], [45601, 6040], ...](images-pell/pell8.gif)
