Maple-Worksheet: Schwingungen und Wellen

Überlagerung von Schwingungen und Wellen

> restart; with(plots):

Überlagerung zweier eindimensionaler Wellen:

> y1:= x -> sin(x - 10*Pi*t):

y2:= x -> 3*sin(x - 4*Pi*t):

W1:= animate(y1(x), x = -2*Pi..2*Pi,
  t = 0..1,
  color = black,
  frames = 200):
W2:= animate (y2(x), x = -2*Pi..2*Pi,
  t = 0..1,
  color = black,
  frames = 200):
Wres:= animate (y1(x)+y2(x), x = -2*Pi..2*Pi,
  t = 0..1,
  color = red,
  frames = 200):

display ([W1, W2, Wres], axes = NONE);

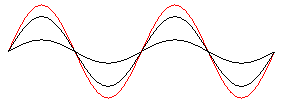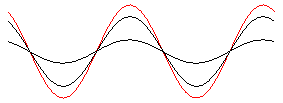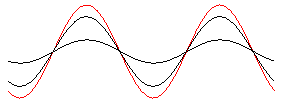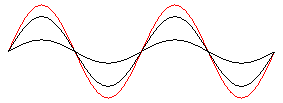
Überlagerung zweier Wellen

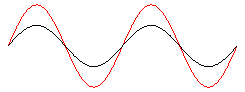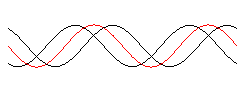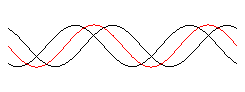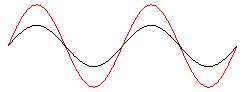
Stehende Welle
durch Überlagerung zweier gegenläufiger Wellen gleicher Wellenlänge und gleicher Frequenz:

> y1:= x -> sin(x - 2*Pi*t):

y2:= x -> sin(x + 2*Pi*t):

Wrechts:= animate (y1(x), x = -2*Pi..2*Pi,
  t = 0..1,
  color = black,
  frames = 150):
Wlinks:= animate (y2(x), x = -2*Pi..2*Pi,
  t = 0..1,
  color = black,
  frames = 150):
Wres:= animate (y1(x)+y2(x), x = -2*Pi..2*Pi,
  t = 0..1,
  color = red,
  frames = 150):

display([Wrechts, Wlinks, Wres], axes = NONE);

stehende Welle

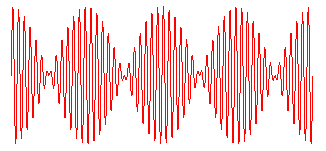
Schwebung
durch Überlagerung zweier Schwingungen mit wenig verschiedenen Frequenzen:

> n1:= 50:

n2:= 54:
y1:= x -> sin(n1*x):
y2:= x -> sin(n2*x):
plot(y1(x)+y2(x), x = -Pi..Pi, color = red, axes = NONE);

Schwebung

Schwingungen im Raum

> animate3d (cos(t*x)*(6-abs(t))*y,

  x = -Pi/2..Pi/2,
  y = -1..1,
  t = -6..6,
  frames = 200);

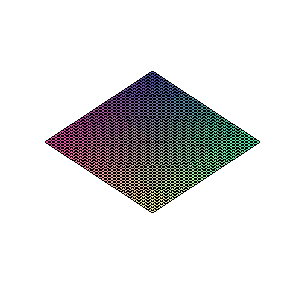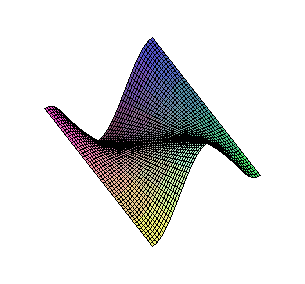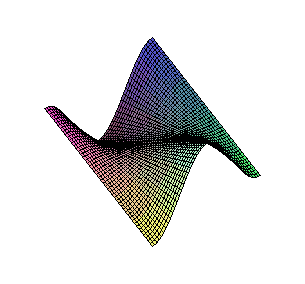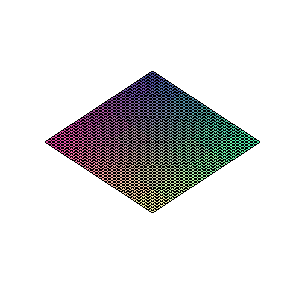
frame 177

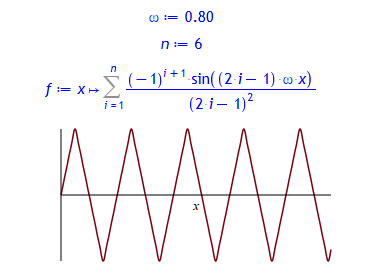
Dreieckschwingung durch Fourier-Synthese:

> omega:= .8;

n:= 6;
f:= x -> Sum((-1)^(i+1)*sin((2*i-1)*omega*x)/(2*i-1)^2, i = 1..n);
plot f(x), x = 0..12*Pi,
  color = red,
  numpoints = 1000,
  tickmarks=[0, 0]);

Dreieckschwingung