Maple-Worksheet: Zahlenfolgen

Zahlenfolgen

> restart;

> interface(showassumed = 0);

(a_n ), Beispiel einer konvergenten Zahlenfolge :

> a:= n -> 1/n^2;

# die ersten 15 Folgenglieder:
seq(a(n), n = 1..15);
# der Grenzwert g_a der Folge (a_n ):
g[a]:= limit(a(n), n = infinity);

(b_n ), Beispiel einer divergenten Zahlenfolge:

> b:= n -> (3*n^2 + 5*n)/(2*n - 1);

seq(b(n), n = 1..15);
g[b]:= limit(b(n), n = infinity);

(c_n ), Beispiel einer oszillierenden Zahlenfolge mit zwei Häufungswerten:

> n:= 'n': assume(n > 0):

t:= n -> (n^3 - n^2)/(n^3 + 5*n^2);

Wenn n eine gerade Zahl ist, dann soll c_n = t_n gelten,
ist n ungerade, so wird c_n = -t_n definiert:

> c:= n -> piecewise(type(n, even), t(n), -t(n)):

seq(c(n), n = 1..20);
plot([seq([n, c(n)], n = 1..100)],
  style = point,
  font = [COURIER, 12],
  labels = ["n", ""]);
g[c][1]:= limit(t(n), n = infinity);
g[c][2]:= limit(-t(n), n = infinity);

Beispiel einer Treppenfunktion:

> liste:= []:

for i from 1 to 4 do
liste:= [op(liste), x <= i and x > i-1, 2*i]:
od:
liste;
treppe:= x -> piecewise(op(liste), 1):
plot(treppe(x), x = -2..7, y = 0..10,
  numpoints = 200,
  font = [COURIER, 12],
  thickness = 2);

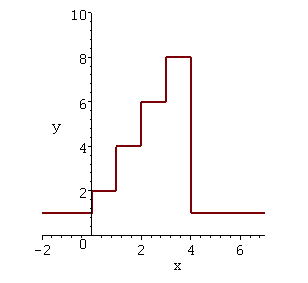
Treppenfunktion

Die Funktionswerte dieser Treppenfunktion, Beispiel einer endlichen Zahlenfolge:

> folge:= 1:

for i from 1 to 4 do
folge:= folge, liste[2*i];
od:
folge, 1;

1, 2, 4, 6, 8, 1