Johann Carl Friedrich Gauß
Johann
Carl Friedrich Gauß, wurde im Jahr 1777 in Braunschweig geboren. Kurz
vor seinem neunzehnten Geburtstag gelang ihm die Entdeckung, dass ein
regelmäßiges 17−Eck nur allein mit Zirkel und Lineal konstruierbar ist.
Die Aufgabe, ein regelmäßiges n−Eck zu konstruieren, ist äquivalent mit der Aufgabe, die Gleichung xn = 1 im Komplexen zu lösen. Ein regelmäßiges n-Eck ist darüberhinaus dann und nur dann mit Zirkel und Lineal konstruierbar, wenn Real- und Imaginärteil der Lösungen dieser Gleichung mit ganzen Zahlen nur unter Verwendung rationaler Rechenoperationen und Quadratwurzeln darstellbar sind. Am 30. März 1796 erkannte Gauß den für diese Aufgabe entscheidenden Zusammenhang zwischen den Wurzeln der Gleichung (xp−1)/(x−1) = 0, wobei p eine Primzahl darstellt. Es heißt, dass aufgrund der Einsicht, welche der regelmäßigen n−Ecke allein mit Zirkel und Lineal konstruiert werden können, Gauß damals endgültig den Entschluss gefasst hat, Mathematik zu studieren.
Schon sein in den Jahren 1796 bis 1798 verfasstes Buch Disquisitiones Arithmeticae, mit welchem Gauß die moderne Zahlentheorie begründet hat, machte ihn zu einem der größten Mathematiker aller Zeiten. Nach seinem Tod im Jahr 1855 ließ der König von Hannover Gedenkmünzen mit dem Bild von Gauß und der Inschrift „Mathematicorum Principi“ („dem Ersten der Mathematiker“) prägen. Viele unveröffentlichte Arbeiten von Gauß wurden erst mit der Entdeckung seiner wissenschaftlichen Tagebücher im Jahre 1898 bekannt.
Bis 1796 wusste man lediglich von der Konstruierbarkeit eines regelmäßigen 3−, 4− bzw. 5−Ecks und wegen der einfachen Möglichkeit, beliebige Winkel nur mit Zirkel und Lineal zu halbieren, war es damit auch möglich, auch regelmäßige 6-, 8−, 10−, 12−, 16−Ecke, u.s.w. zu konstruieren.
Eine Zeichenoperation mit Hilfe eines Zirkels und eines Lineals soll genau dann zulässig heißen, wenn es sich um eine der folgenden elementaren Zeichenoperationen oder eine endliche Folge dieser elementaren Zeichenoperationen handelt:
- Zeichnen einer beliebig langen und geraden Linie
- Zeichnen einer beliebig langen und geraden Linie durch einen Punkt
- Zeichnen einer beliebig langen und geraden Linie durch zwei Punkte
- Zeichnen eines Kreises um einen Punkt mit einem beliebig, aber
fest gewählten Radius
Eine Konstruktion mit Zirkel und Lineal beinhaltet ausschließlich die folgenden Dinge:
- das Zeichnen eines beliebigen Punktes
- das Zeichnen eines Punktes auf einer Linie
- zulässige Zeichenoperationen
- Bezeichnung von Punkten, Strecken, Geraden und Kreisen
Die elementaren geometrischen Grundkonstruktionen, wie zum Beispiel die Konstruktion einer Mittelsenkrechten oder einer Winkelhalbierenden, lassen sich alle lediglich mit Zirkel und Lineal durchführen. Mit Hilfe solcher Grundkonstruktionen ist beispielsweise auch ein regelmäßiges 5-Eck konstruierbar:
Ausgangsfigur der Konstruktion eines regelmäßigen 5−Ecks ist ein Kreis mit dem Durchmesser AB und der Senkrechten auf diesem Durchmesser durch den Kreismittelpunkt M. Diese Senkrechte schneidet den gegebenen Kreis im Punkt S, dem ersten Punkt des zu konstruierenden regelmäßigen 5−Ecks. Um den Mittelpunkt zwischen A und M wird ein Kreis geschlagen, und zwar so, dass dieser Kreis durch S läuft. Der zuletzt gezeichnete Kreis schneidet den Durchmesser AB im Punkt N. Der Kreis um S mit dem Radius |SN| schneidet den Ausgangskreis im zweiten Punkt des gesuchten 5−Ecks. Der Kreis um diesen zweiten Eckpunkt T mit demselben Radius |SN| liefert den dritten Eckpunkt U, usw.
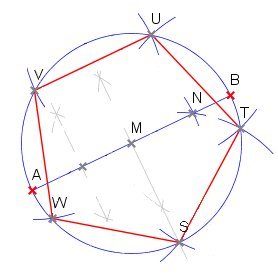
Bezeichnet man |MS| mit r und die Kantenlänge des konstruierten 5−Ecks mit x, dann folgt mit einfacher Rechnung unter Benutzung des Satzes von Pythagoras
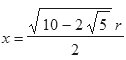
Die Eckpunkte eines regelmäßigen 5−Ecks mit r = 1 entsprechen den komplexen Lösungen der Gleichung x5 = 1:
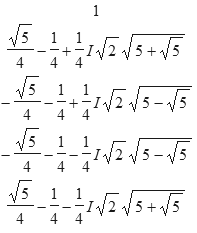
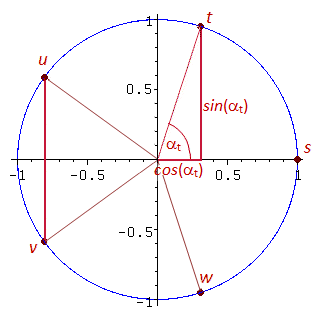
Wenn man diese fünf Lösungen in der Gauß’schen Ebene veranschaulicht, erkennt man den Zusammenhang mit der eben abgeleiteten Formel für die Kantenlänge x. Außerdem sieht man, dass zur Berechnung aller Lösungen s, t, u, v und w lediglich der Kosinus des Winkels αt bekannt sein muss. Alles andere lässt sich hieraus herleiten.
Gauß hat mit von ihm neu entwickelten Methoden nachweisen können, dass
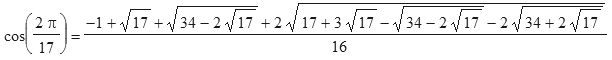
und damit nach dem eingangs Gesagten gezeigt, dass ein regelmäßiges 17−Eck nur mit Zirkel und Lineal konstruierbar ist.
Darüberhinaus hat Gauß ein hinreichendes Kriterium für die Konstruierbarkeit eines regelmäßigen n−Ecks bewiesen: n muss eine Primzahl sein, die folgender Formel genügt:
mit k ∈∈ ℕ.
| 1777 | Gauß wird am 30. April in Braunschweig geboren. |
| 1792 | Studium am Collegium Carolinum in Braunschweig (bis 1795). |
| 1795 | Studium an der Universtät Göttingen (bis 1798). Entwicklung der Methode der kleinsten Quadrate. |
| 1796 | Beweis der Konstruierbarkeit eines regelmäßigen
17-Ecks. Gauß beginnt, wissenschaftliche Tagebücher zu führen. |
| 1799 | Beweis des Fundamentalsatzes der Algebra in seiner Doktorarbeit. |
| 1801 | Veröffentlichung der Disquisitiones Arithmeticae
(Arithmetische Abhandlungen): (1) Theorie der Kongruenzen; (2) Theorie der quadratischen Formen; (3) Kreisteilung. Beweise des von Euler entdeckten quadratischen Reziprozitätsgesetzes. Berechnung der Bahn des Zwergplaneten Ceres. |
| 1807 | Gauß wird Professor in Göttingen und Direktor der dortigen Sternwarte. |
| 1812 | Veröffentlichung zu Untersuchungsergebnissen über die hypergeometrische Reihe. |
| 1818 | Abhandlung über Säkularstörungen. Gauß erhält den Auftrag zur Vermessung des Königreiches Hannover. |
| 1820 | Studium der nicht-euklidischen Geometrie in den
1820er Jahren. Entwicklung des Heliotropen. |
| 1827 | Disquisitiones generales circa superficies curvas (Allgemeine Untersuchungen über gekrümmte Flächen). |
| 1832 | Gauß und Wilhelm Eduard Weber entwickeln gemeinsam das
cgs-Einheitensystem. Forschungen in den 1830er Jahren zum Magnetismus zusammen mit Weber. |
| 1855 | Gauß stirbt am 23. Februar in Göttingen. |
| 1898 | Die Tagebücher von Gauß werden entdeckt. |
Wikipedia: Carl Friedrich Gauß
Carl Friedrich Gauß’ Untersuchungen über höhere Arithmetik
