Skalarprodukt
definiert in: Vektor/ Skalarprodukt von Vektoren
Die Definition des Skalarprodukts liefert eine Möglichkeit, zwei Vektoren miteinander zu multiplizieren. Das Ergebnis des Skalarprodukts zweier Vektoren ist kein Vektor, sondern eine Zahl:
Gegeben seien zwei von o verschiedene, aber ansonsten beliebige Vektoren a, b ∈∈ ℙ, die den Winkel α einschließen. Dann heißt
a•b = |a|·|b|·cos(α)
das Skalarprodukt von a und b. Ist a = o oder b = o, dann setzt man a•b = 0.
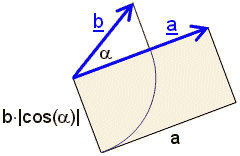
Für 0°≤ α < 90° und 270° < α ≤ 360° ist a•b positiv; für 90° < α < 270° ist a•b negativ; a•b = 0, wenn α = 90° oder α = 270°.
Hiermit lässt sich der geometrische Sachverhalt, dass zwei geometrische Objekte senkrecht zueinander stehen, auch analytisch ausdrücken:
a ⊥ b ⇔ a•b = 0 mit a, b ǂ o
Außerdem folgt direkt aus der Definition des Skalarprodukts a•a = |a|2 für alle a ∈∈ ℙ, kurz geschrieben:
a2 = a2 für alle a ∈∈ ℙ.
Physikalisch ist das Skalarprodukt überall dort bedeutsam, wo es um die Berechnung von Energiemengen geht und hierbei gerichtete Größen eine Rolle spielen. Zwei Beispiele: Für die Verschiebung eines Körpers um einen gewissen Streckenabschnitt Δs durch eine konstante Kraft F muss insgesamt die Energie ΔW = F•Δs aufgebracht werden. ändert irgendein sich mit der Geschwindigkeit v gleichförmig bewegtes System seinen Impuls um ΔP, dann nimmt es hierbei den Energiebetrag ΔW = v•ΔP auf.
→ Vektorprodukt → Index
