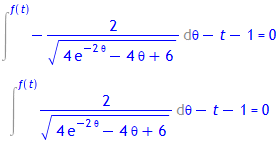Differentialgleichungen
> restart;
interface(displayprecision = 4):
Beispiel 1 (die e-Funktion):
> DGl1:= diff(f(x), x) = f(x);
![]()
Lösung der Differentialgleichung DGl1:
> dsolve(DGl1 , f(x));
![]()
Die Probe:
![]()
![]()
Lösung der Gleichung DGl1 unter Beachtung der Bedingung f(2) = 4:
![]()
> evalf(%, 4);
![]()
Beispiel 2 (logistisches Wachstum):
> restart;
> DGl2:= diff(f(t), t) = k*f(t)*(S - f(t));
![]()
> dsolve(DGl2, f(t));
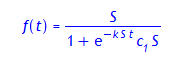
> f:= t -> 100/(1 + 200*exp(-4*t));

> plot(f(t), t = 0..3, font = [COURIER, 12]);

Beispiel 3 (nichtlineare Differentialgleichung):
> restart;
> Df:= t -> diff(f(t), t);
DDf:= t -> diff(Df(t), t);
DGl:= DDf(t) + a*Df(t)^2 + b*f(t) - c = 0;
loesg:= dsolve(DGl, f(t)):
nops(op(loesg))*'Lösungen';
loesg1:= loesg[1];
loesg2:= loesg[2];
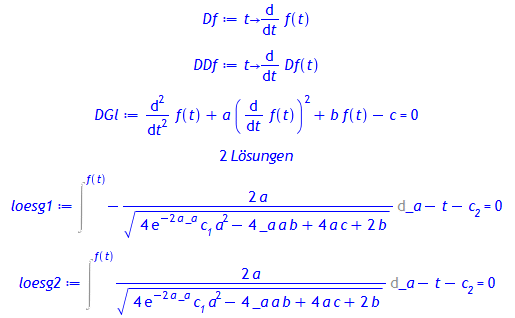
> a:= 1: b:= 1: c:= 1:
subs(_a = theta, loesg1);
subs(_a = theta, loesg2);