Maple-Worksheet: Quantenobjekt im Potentialkasten

Quantenobjekt im Potentialkasten

> restart; with(plots):

interface(showassumed = 0):
interface(displayprecision = 3):
fnt:= 'font = [COURIER, 12]':

Kastenpotential V(x) mit endlicher Tiefe und beliebig, aber fest gewählter Länge 2a:

> assume(Vo, positive):

assume(x, real):
V:= x -> piecewise(abs(x)<=a, -Vo, abs(x)>a, 0);

a:= 1:
plot (subs (Vo = 1.5, V(x)), x = -2*a..2*a,
thickness = 2,
  fnt,
adaptive = true,
size = [350, 200],
  numpoints = 5000,
color = red,
  labels = ["", ""],
  tickmarks = [4, 0],
  view = [-2..2, -2..0]);

kasten2

Stationäre Schrödinger-Gleichung für ein Quantenobjekt im linearen Potentialkasten:

> assume(hbar, positive): # Reduzierte Planck’sche Konstante

assume(m, positive): # Masse des Quantenobjektes
SG:= -C*diff(psi(x), x$2) + V(x)*psi(x) = E*psi(x);
'C' = hbar^2/(2*m);
'hbar' = h/(2*Pi);

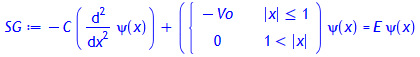
kasten3
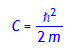
C = hbar^2/(2m)

Lösen der Schrödinger-Gleichung unter den gegebenen Voraussetzungen:

> assume(E, negative):

# Die Lösungen dieser Gleichung müssen normierbar sein!
dsolve(SG);

Psi(x)

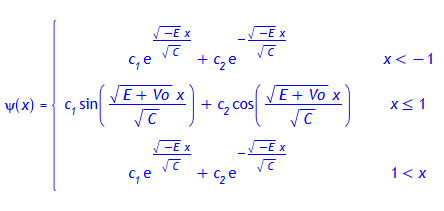
Ψ(x) muss für große bzw. kleine Werte von x verschwinden, also ergibt sich:

> psiL:= x -> F*exp(kappa*x); # für x < -a

psiM:= x -> G*cos(k*x)+H*sin(k*x); # für |x| <=a
psiR:= x -> J*(exp(-kappa*x)); ; # für x > a
'k' = sqrt((Vo+E)/C);
'kappa' = sqrt(-E/C);

psiL; psiM; psiR
k = sqrt((Vo + E)/C
kappa = sqrt(-E/C)

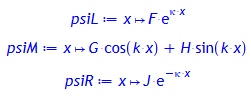
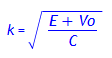
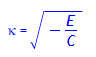
Es ist zu fordern, dass die Funktionen Ψ und Ψ' insbesondere an den Stellen x = -a und x = a stetig sind:

> a:= 'a':

gl1:= subs(x=-a, psiL(x)) = subs(x=-a, psiM(x));
gl2:= subs(x=a, psiR(x)) = subs(x=a, psiM(x));
gl3:= subs(x=-a, diff(psiL(x),x) = subs(x=-a, diff(psiM(x),x)));
gl4:= subs(x=a, diff(psiR(x),x) = subs(x=a, diff(psiM(x),x)));

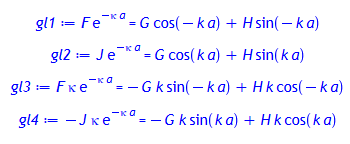
gl1, gl2, gl3, gl4

Bei den nächsten Rechenschritten kann Maple nicht helfen:

> gl1 + gl2;

gl3 + gl4;

gl1 - gl2;
gl3 - gl4;

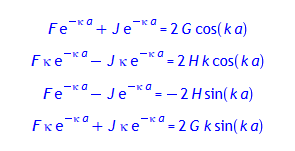
Gleichungen

Hieraus erhält man:

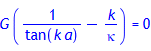
> G*(1/tan(k*a) - k/kappa) = 0;

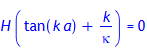
H*(tan(k*a) + k/kappa) = 0;

G(1/tan(ka) - k/kappa) = 0
H(tan(ka) + k/kappa = 0

Unter der Annahme, dass G nicht 0 ist, muss notwendigerweise H gleich 0 sein und es folgt:

> psiM:= x -> G*cos(k*x): # für |x| <=a

psiLR:= x -> G*cos(k*a)*exp(kappa*(a-abs(x))): # für |x| > a

psi[cos]:= x -> piecewise (abs(x)<=a, psiM(x), abs(x)>a, psiLR(x)):
'psi[cos](x)' = psi[cos](x);

Psi[cos](x)

Unter der Annahme, dass H nicht 0 ist, muss notwendigerweise G gleich 0 sein und es folgt:

> psiM:= x -> H*sin(k*x): # für |x| <=a

psiLR:= x -> signum(x)*H*sin(k*a)*exp(kappa*(a-abs(x))): # für |x| > a

psi[sin]:= x -> piecewise(abs(x)<=a, psiM(x), abs(x)>a, psiLR(x)):
'psi[sin](x)' = psi[sin](x);

Psi[sin](x)

Finden eines Zusammenhanges zwischen k und κ:

> C:= hbar^2/(2*m); # siehe oben

k:= sqrt((Vo+E)/C): # siehe oben
kappa:= sqrt(-E/C): # siehe oben
simplify (k^2 + kappa^2); # nur abhängig von Vo, aber nicht von E !
'ko' = sqrt(%);

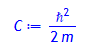
C:= hbar^2/(2m)
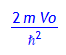
2*m*Vo/hbar^2
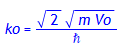
ko = sqrt(2)*sqrt(m*Vo)/hbar

Hieraus ergibt sich:

> `k:= 'k': ko:= 'ko':

kappa:= sqrt(ko^2 - k^2);

Im Falle der um x = 0 symmetrischen Eigenlösungen Ψ_cos(x) folgt:

> k:= 'k': ko:= 'ko': a:= 'a':

tan(k*a) = kappa/k;
tan(k*a) = subs({ko=ko*a, k=k*a}, kappa/k); # erste Eigenwertgleichung

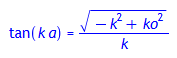
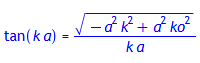
tan(ka)
tan(ka)

Im Falle der um x = 0 antisymmetrischen Eigenlösungen Ψ_sin(x) folgt:

> k:= 'k': ko:= 'ko': a:= 'a':

tan(k*a) = -k/kappa;
tan(k*a) = subs({ko=ko*a, k=k*a}, -k/kappa); # zweite Eigenwertgleichung

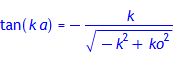
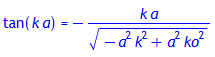
tan(ka)
tan(ka)

Prozedur nur numerischen Bestimmung der Nullstellen der Eigenwertgleichungen:

> eqsolve:= proc(equation, z0, imin, imax, dz, dig, dpr)

  local zeros, zero, i, liste;
  Digits:= dig:
  interface(displayprecision = dpr):
  zeros:= {}:

  for i from imin to imax do
    zero:= fsolve (equation, z = z0 + i*dz):
    if (not evalb(zero in zeros) and zero > 0) then
      zeros:= zeros union {zero}:
    fi:
  od:

  liste:= sort (convert (evalf(zeros), list));
end:

Die Daten für ein konkretes Beispiel:

> m:= evalf(ScientificConstants[Constant](electron_mass)): # in kg

hb:= 'Planck_constant_over_2pi':
hbar:= evalf(ScientificConstants[Constant](hb)): # in Js
Vo:= 16E-18; # in J
ko:= sqrt(2*m*Vo/hbar^2); # in 1/m
a:= 1E-10; # in m
zo:= ko*a; # dimensionslos
'z' = 'k*a';

z = ka

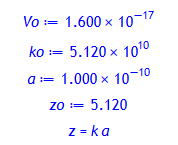
Visualisierung und Berechnung der Lösungen der zwei Eigenwertgleichungen für das genannte Beispiel:

> f[cos]:= z -> sqrt(zo^2 - z^2)/z:

f[sin]:= z -> -z/sqrt(zo^2 - z^2):

eq1:= tan(z) = f[cos](z):
eq2:= tan(z) = f[sin](z):

opts:= 'color=[black,red,blue], view=[0..zo+1,-10..8], discont=true':
plot([tan(z), f[cos](z), f[sin](z)], z = 0..zo+1, opts, fnt);

lgn[cos]:= eqsolve (eq1, 0, 1, 2*trunc(zo+1), 0.5, 20, 4);
lgn[sin]:= eqsolve (eq2, 0, 1, 2*trunc(zo+1), 0.5, 20, 4);

kasten25
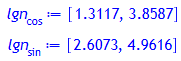
Eigenlösungen

Auflistung aller erlaubten z-Werte:

> zValues:= sort([op(lgn[cos]), op(lgn[sin])]);

num:= nops(zValues):

Auflistung der zugehörigen k-Werte:

> liste:= []:

for i from 1 to num do
k||i:= zValues[i]/a:
liste:= [op(liste), k||i]:
od:
kValues:= liste;

Auflistung der zugehörigen Energiewerte:

> liste:= []:

C:= hbar^2/(2*m):
for i from 1 to num do
E||i:= (k||i)^2*C - Vo;
kappa||i:= sqrt(-E||i/C):
liste:= [op(liste), E||i]:
od:
EValues:= liste;

Berechnung der zugehörigen Wellenfunktionen Ψ_n(x):

> N:= 'N':

for i from 1 to num by 2 do
psiM||i(x):= N*cos(k||i*x):
psiLR||i(x):= N*cos(k||i*a)*exp(kappa||i*(a-abs(x))):
od:

for i from 2 to num by 2 do
psiM||i(x):= N*sin(k||i*x);
psiLR||i(x):= signum(x)*N*sin(k||i*a)*exp(kappa||i*(a-abs(x)));
od:

for n from 1 to num do
p[n](x):= piecewise(abs(x)<=a, psiM||n(x), abs(x)>a, psiLR||n(x)):
od:
for n from 1 to num do psi[n](x):= p[n](x); od;

Psi[1](x); Psi[2](x); Psi[3](x); Psi[4](x);

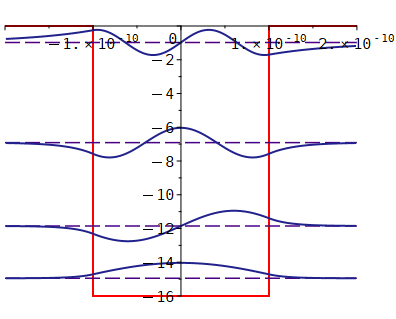
Normierung und Zeichnung der Wellenfunktionen:

> # Zunächst müssen die Wellenfunktionen berechnet worden sein.

sc:= 1E-5: # Skalierungsfaktor
for n from 1 to num do
v:= solve (int((psi[n](x))^2, x=-infinity..infinity) = 1, N)[1]:
psi[n](x):= subs(N = v*sc, psi[n](x)):
od:

y0:= -Vo*1E18:
V:= x -> piecewise(abs(x)<=a, y0, abs(x)>a, 0):
kasten:= plot(V(x), x = -2*a..2*a,
thickness = 2,
color = red,
adaptive = true,
  numpoints = 5000,
  labels = ["", ""]):

niveaus:= NULL:
for n from 1 to num do
l[n]:= plot (E||n*1E18, x = -2*a..2*a,
    color = indigo,
   linestyle = dash):
niveaus:= niveaus, l[n]:
od:

kurven:= NULL:
for n from 1 to num do
K[n]:= plot(E||n*1E18 + psi[n](x), x = -2*a..2*a,
     color = navy,
     fnt,
     thickness = 2):
kurven:= kurven, K[n]:
od:

display ([kasten, niveaus, kurven],
view=[-2*a..2*a,0..y0],
size = [450, 300]);

display