dh-Materialien Einführung in Maple    Anwendungen
|  Home  |  Back  |  <   >  |

Mathematik
 

Einführung in Maple
  Hinweise
  Übersicht
  Übungen
  Anwendungen
  Stichworte
  Download
 

Parabel durch drei Punkte A, B und C

> 
 restart;

Gegeben seien drei Punkte A(x1| y1), B(x2| y2) und C(x3| y3).
Gesucht ist die Gleichung  y = ax2 + bx + c  derjenigen Parabel, die durch A, B und C läuft.

> 
 gl1:= x[1]^2*a + x[1]*b + c - y[1] = 0:
gl2:= x[2]^2*a + x[2]*b + c - y[2] = 0:
gl3:= x[3]^2*a + x[3]*b + c - y[3] = 0:  
gl1; gl2; gl3;

x[1]^2*a+x[1]*b+c-y[1] = 0
x[2]^2*a+x[2]*b+c-y[2] = 0
x[3]^2*a+x[3]*b+c-y[3] = 0

Lösen des Gleichungssystems {  gl1, gl2,  gl3 }:

> 
 lgn:= solve ({gl1, gl2, gl3}, {a,b,c}):
assign (lgn): a:= a; b:= b; c:= c;



> 
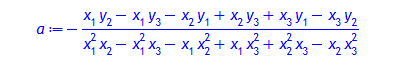
 f:= unapply ([a,b,c], [x[1], y[1], x[2], y[2], x[3], y[3]]):

Beispiel: Welche Parabel läuft durch (1|2), (-2|8) und (-1|4) ?
Antwort: Es ist diejenige Parabel mit a = 1, b = -1 und c = 2.

> 
 f(1, 2, -2, 8, -1, 4);

[1, -1, 2]
Copyright

Valid HTML 4.01 Transitional
|  Home  |  Back  |  Top  |