Teilspannungen einer Siebkette
| ohmscher Widerstand | R = | 100 Ω |
| Induktivität | L = | 2 H |
| Kapazität | C = | 20 μF |
| Frequenz | f = | 50 Hz |
| Effektivspannung | U = | 20 V |
> restart;
sqrt2:= evalf(sqrt(2)):
interface(displayprecision = 4):
interface(displayprecision = 4):
Die in diesem Zusammenhang relevanten physikalischen Formeln:
> XL:= omega*L;
XC:= 1/(omega*C);
Z:= sqrt(R^2 + (XL-XC)^2);
omega:= 2*Pi*f;
Z:= sqrt(R^2 + (XL-XC)^2);
omega:= 2*Pi*f;
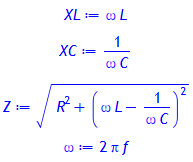
Berechnung der Kreisfrequenz in Hertz:
> f:= 50*Hz;
omega:= evalf(omega, 4);
![]()
Berechnung der Blindwiderstände XL und XC und des Scheinwiderstandes Z in Ohm:
> omega:= omega/Hz:
L:= 2:
XL:= evalf(XL*Omega, 4);
C:= 20E-6:
XC:= evalf(XC*Omega, 4);
R:= 100:
Z:= evalf(Z*Omega, 4);
XL:= evalf(XL*Omega, 4);
C:= 20E-6:
XC:= evalf(XC*Omega, 4);
R:= 100:
Z:= evalf(Z*Omega, 4);
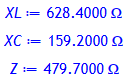
Berechnung der Stromstärke Ieff in Ampere und der Spannungsamplituden in Volt:
> Ieff:= evalf(20/(Z/Omega)*A, 4);
U[L0]:= evalf((XL/Omega)*(Ieff/A)*sqrt2*V, 4);
U[C0]:= evalf((XC/Omega)*(Ieff/A)*sqrt2*V, 4);
U[R0]:= evalf((100)*(Ieff/A)*sqrt2*V, 4);
U[C0]:= evalf((XC/Omega)*(Ieff/A)*sqrt2*V, 4);
U[R0]:= evalf((100)*(Ieff/A)*sqrt2*V, 4);

Die Teilspannungen UL, UC und UR in Abhängigkeit von der Zeit t:
> UL(t):= (U[L0]/V)*cos((omega)*t);
UC(t):= -(U[C0]/V)*cos(omega*t);
UR(t):= (U[R0]/V)*sin(omega*t);
UR(t):= (U[R0]/V)*sin(omega*t);
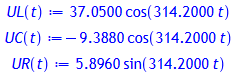
Die Gesamtspannung Uges:
> Uges(t):= UL(t) + UC(t) + UR(t);
![]()
> plot ([UC(t),UR(t),UL(t),Uges(t)], t = 0..0.03, y = -40..40,
labels = [t, ""],
thickness = 1,
font = [Courier, 10],
labelfont = [Courier, 13],
size = [350, 300],
color = [blue, red, magenta, navy]);
thickness = 1,
font = [Courier, 10],
labelfont = [Courier, 13],
size = [350, 300],
color = [blue, red, magenta, navy]);

