Maple-Worksheet: Türme von Hanoi

Türme von Hanoi

> restart; with(plots): with(plottools):

Anfangssituation mit n Scheiben:

> n:= 3:

tow[1]:= []:
for i from n by -1 to 1 do
tow[1]:= [op(tow[1]), i]:
od:
tow[2]:= []:
tow[3]:= []:
tow[1], tow[2], tow[3];

Prozedur zum Zeichnen der drei Türme:

> drawTowers:= proc(k)

  global tow, plotTow:
  local i, j, r, p:
  p:= []:
  for i from 1 to 3 do
    if nops(tow[i]) <> 0 then
      for j from 1 to nops(tow[i]) do
        r:= op(j, tow[i]):
        p:= [op(p), cylinder([(i-2)*(2*n+1),0,j], r, 1)]:
      od:
    fi:
  od:
  for i from 1 to 3 do
    p:= [op(p), cylinder([(i-2)*(2*n+1),0,1], n, 0.005)]:
  od:
  plotTow[k]:= p:
end:

Optionen für die Darstellung der drei Türme:

> opts:= 'view = [-3*n-1..3*n+1, -3*n-1..3*n+1, 1..n+4],

color = gold,
axes = none,
size = [400, 400],
orientation = [-98, 65]':

Darstellung der Anfangssituation:

> drawTowers(0):

display(plotTow[0], opts);

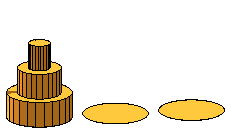
Rekursive Prozedur zum Bewegen der Scheiben:

> m:= 0:

moveDisk:= proc(i, a, b, c)
  global tow, m:
  local n, actualDisk:
  if i > 0 then
    moveDisk i-1, a, c, b):
    n:= nops(tow[a]):
    actualDisk:= op(n, tow[a]):
    tow[a]:= subsop(n=NULL, tow[a]):
    tow[c]:= [op(tow[c]), actualDisk]:
    print(tow[1], tow[2], tow[3]):
    m:= m + 1:
    drawTowers(m):
    moveDisk (i-1, b, a, c):
  fi:
end:

Schrittweises Bewegen der Scheiben:

> moveDisk(n, 1, 2, 3):

tuerme3

Darstellung der Spielschritte:

> display([seq(display(plotTow[i]), i = 0..m)],

opts,
insequence = true);

Minimale Anzahl der Spielschritte in Abhängigkeit von n:

> for n from 1 to 15 do

print(2^n - 1);
od:

tuerme15