Fläche
Man begegnet Flächen in der Regel zunächst im Zusammenhang mit Körpern und dann mit ebenen Figuren. Tatsächlich in dieser Reihenfolge, denn ein Kind lernt zuerst, die Oberfläche von Bällen, Bauklötzen und anderen Dingen zu be-greifen, bevor es in der Schule die Eigenschaften von Rechtecken, Dreiecken, Kreisen und anderen geometrischen Figuren untersucht.
Es ist offensichtlich von großem Interesse, den Inhalt von Flächen berechnen bzw. messen zu können: ein Landwirt möchte wissen, wieviel Saatgut er kaufen muss, um seine Ackerflächen zu bestellen; ein Dachdecker muss die Gesamtfläche eines Hausdaches wissen, um die benötigte Menge an Dachziegeln bestimmen zu können; die Fläche eines Grundstücks muss vermessen werden, um den entsprechenden Grundsteuerbetrag festlegen zu können; und so fort.
Flächen einfacher ebener Figuren
 Am einfachsten ist die Berechnung des Inhalts AR einer
Rechteckfläche. Werden die Längen der Rechteckseiten mit a bzw. mit b
bezeichnet, so gilt AR = a·b.
Im Abschnitt Rechteckflächen wird bewiesen,
dass diese Formel immer gültig ist, unabhängig davon, wie lang die
Seiten des jeweiligen Rechtecks sind.
Am einfachsten ist die Berechnung des Inhalts AR einer
Rechteckfläche. Werden die Längen der Rechteckseiten mit a bzw. mit b
bezeichnet, so gilt AR = a·b.
Im Abschnitt Rechteckflächen wird bewiesen,
dass diese Formel immer gültig ist, unabhängig davon, wie lang die
Seiten des jeweiligen Rechtecks sind.
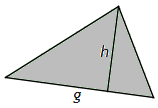
Für den Inhalt AD einer Dreiecksfläche gilt AD = 12·g·h (→ Beweis). Hierbei bedeutet g die Länge einer der Dreiecksseiten bzw. h die Länge der Höhe auf der jeweils ausgewählten Dreiecksseite:
Polygonflächen
Jedes einfache Polygon ist triangulierbar (→ Beweis). Das bedeutet: Die Fläche einer ebenen Figur, deren Rand von einem einfachen Polygon gebildet wird, lässt sich stets in sich nicht überlappende Dreiecksflächen zerlegen. Diese Zerlegung ist nicht eindeutig, wie das folgende einfache Beispiel zeigt:


Die Formel zur Berechnung des Inhaltes AP einer in n Dreiecksflächen zerlegten Polygonfläche ist schnell gefunden: AP = n∑i = 1Ai. Hierbei bezeichnet Ai den Flächeninhalt des i-ten Dreiecks der Zerlegung. AP ist unabhängig von der gewählten Zerlegung der jeweiligen Polygonfläche stets eindeutig bestimmt (→ Beweis).
Kreisumfang und Kreisfläche
Gegeben sei ein Kreis mit dem Radius r. Die Kreislinie lässt sich nach X74 beliebig gut durch ein im Kreis einbeschriebenes regelmäßiges n-Eck approximieren. Entsprechenderweise kann die Kreisfläche beliebig gut durch die Fläche eines solchen n-Ecks approximiert werden:

Unter Verwendung der im Diagramm erklärten Bezeichnungen gilt für den Flächeninhalt An des n-Ecks
An = n·(12·s·rn) = 12·Un·rn.
Für n → ∞ strebt Un gegen den Umfang U des Kreises bzw. rn gegen den Kreisradius r. U ist proportional zum Kreisdurchmesser (→ Beweis). Setzt man voraus, dass die Proportionalitätskonstante die Kreiszahl π ist, so folgt mit U = 2π·r unter Beachtung von F2(ii) für die Kreisfläche A sofort A = π·r2.
Oberflächen geometrischer Körper
Die Formeln zur Berechnung der Inhalte von Oberflächen geometrischer Körper sind in einfachen Fällen auf die Flächeninhaltsformeln ebener Figuren zurückzuführen.
Beispielsweise ist der abgewickelte Mantel eines geraden Zylinders ein Rechteck. Ist r der Radius der Grundfläche des Zylinders und h die Höhe des Zylinders, so ist demnach die Mantelfläche gleich 2πrh.
Der abgewickelte Mantel eines geraden Kreiskegels ist ein Kreissektor. Der Kreissektorradius ist gleich der Länge der Mantellinie des Kegels; die Bogenlänge des Kreissektors ist gleich dem Umfang des Grundkreises des Kegels.
Flächen unter Kurven
Von ganz besonderer Bedeutung sind die Flächen zwischen den Graphen bestimmter Funktionen und der jeweiligen Rechtsachse. Das nachstehende Diagramm etwa beschreibt die Bewegung eines sich beschleunigenden Körpers, wobei mit v seine Geschwindigkeit in Abhängigkeit von der Zeit t gemeint ist. Die im Diagramm dargestellte Fläche bedeutet die zwischen den Zeitpunkten t0 und t1 vom Körper zurückgelegte Strecke.
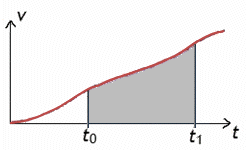
Zur Berechnung solcher Flächen benötigt man die Integralrechnung.
Gekrümmte Flächen im Raum
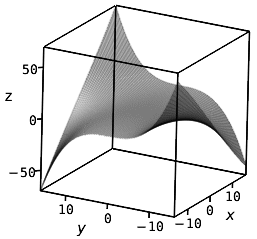
Flächen im Raum können durch Gleichungen beschrieben werden. Beispielsweise entsprechen die Lösungen (x; y; z) der Gleichung 1000·z = x·(x2 + y3) Punkten, die auf einer unbegrenzt ausgedehnten Fläche liegen. Nachstehend ist ein Stück dieser Fläche abgebildet:
Mit der Gleichung z = −√25 − x2 − y2 wird eine Halbkugel mit dem Radius 5 beschrieben:
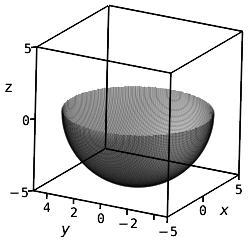
Beide Flächen haben zwei Seiten, das heißt, es sind orientierte Flächen: Die Halbkugel besitzt eine Innen- und eine Außenfläche; bei der erstgenannten Fläche gibt es ein „unten“ und ein „oben“.
Das Möbiusband (eine von Johann B. Listing und August F. Möbius unabhängig voneinander 1858 erstmals beschriebene Fläche) ist das klassische Beispiel für eine nicht-orientierte Fläche:
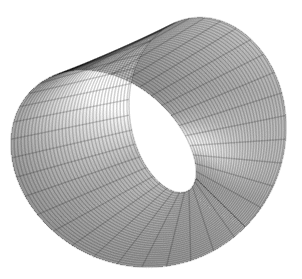
Das hier dargestellte Exemplar kann in parametrisierter Form beschrieben werden:
x(r, α) = cos(R
+ r2·cos α2)·cos(α)
y(r, α) = cos(R
+ r2·cos α2)·sin(α)
z(r, α) = r2·sin(α2)
r = −90..90; α
= 0..2π;
R = 120.
Der Inhalt einer Fläche wird immer relativ zum Inhalt einer Einheitsfläche angegeben. Beispielweise bedeutet die Aussage, dass der Flächeninhalt eines bestimmten Rechtecks 13 cm2 beträgt, dass dieses Rechteck 13-mal größer ist als das Einheitsquadrat mit der Seitenlänge 1 cm.
Grundsätzlich kann man irgendeine Einheitsfläche benutzen, um Rechteckflächen auszumessen. Will man etwa zwei vorgegebene Rechtecke bezüglich ihres Flächeninhalts miteinander vergleichen, hat man nur herauszufinden, wie oft die geeignet gewählte, aber im Prinzip beliebige Einheitsfläche in die eine bzw. in die andere Fläche passt.
Entspricht eine Rechteckfläche exakt einem ganzzahligen Vielfachen der gewählten Einheitsfläche, ist das Bestimmen des Flächeninhalts besonders einfach. Beispielsweise beträgt der Flächeninhalt des nachstehend abgebildeten Rechtecks genau 6Q unter Verwendung des Einheitsquadrats mit dem Flächeninhalt Q.

Eine Formel zur Berechnung des Flächeninhalts A eines Rechtecks ist schnell gefunden:
A = α·β Q ,
wobei die eine Seite des Einheitsquadrats genau β-mal in die erste Seite des Rechtecks und die andere Seite des Einheitsquadrats genau α-mal in die zweite Rechteckseite passt. Im obigen Beispiel ist β = 2 und α = 3.
Wenn die Längenmaßzahlen α und β nicht ganzzahlig sind, ist der Flächeninhalt nicht einfach durch Abzählen der Einheitsquadrate zu haben:

Die Flächeninhaltsformel gilt aber auch dann! Das kann sogar bewiesen werden, indem der Flächeninhalt eines solchen Rechtecks als Grenzwert verstanden wird. Wie man sich diesem Grenzwert nähern kann, soll anhand des folgenden Beispiels erläutert werden.
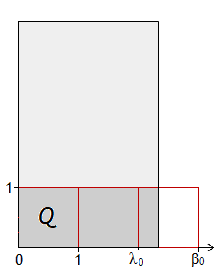
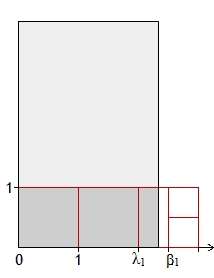

Die dunkelgraue Teilfläche kann näherungsweise durch eine gewisse Anzahl von Flächenstücken ersetzt werden, deren Inhalte entweder gleich Q oder ganzzahlige Teiler von Q sind (im Beispiel zunächst Viertel, dann Sechzehntel von Q und so fort).
λ0·Q, λ1·Q, λ2·Q, ... (im Beispiel 2Q, 2Q+0·Q4, 2Q+4·Q16, ...) ist der Anfang einer monoton wachsenden Folge von Flächeninhalten. Ein Folgenglied λn·Q approximiert den Flächeninhalt AT der dunkelgrauen Teilfläche umso besser, je höher n gewählt wird, bleibt aber immer kleiner als AT, wenn man sich − in der in den Bildern beschriebenen Weise − „von links“ der rechten senkrechten Rechteckseite annähert.
β0·Q, β1·Q, β2·Q, ... (im Beispiel 3Q, 3Q−2·Q4, 3Q−0·Q16, ...) ist der Anfang einer monoton fallenden Folge von Flächeninhalten. Jedes Glied dieser Folge ist größer als AT, wenn man sich „von rechts“ der rechten senkrechten Rechteckseite annähert.
Mit den konvergenten Zahlenfolgen (λn)n∈∈ℕ und (βn)n∈∈ℕ hat man eine Intervallschachtelung ([λn, βn])n∈∈ℕ. Wird der (eindeutig bestimmte) innere Punkt dieser Intervallschachtelung und gemeinsame Grenzwert beider Folgen mit β bezeichnet, so ist der Inhalt der dunkelgrauen Fläche gleich β·Q. β ist die Längenmaßzahl der waagerechten Seite des vorgegebenen Rechtecks bezüglich Q.
Führt man die eben beschriebene Prozedur ein zweites Mal in vertikaler Richtung durch, so erhält man unter Benutzung der Längenmaßzahl α der vertikalen Rechteckseite schlussendlich die Formel A = α·β Q für jedes beliebige Rechteck.

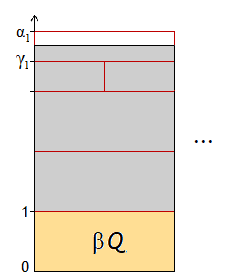
In der obigen Argumentation wurde stillschweigend angenommen, dass es sich beim Flächeninhalt (nicht nur bei Rechtecken, sondern bei beliebigen Flächen) um eine Größe handelt. Dies bedeutet, dass alle Maßzahlen nicht-negativ sein dürfen und für beliebige Maßzahlen η und ν bezüglich Q das Folgende gilt:
| (I) | (η + ν)·Q = η·Q + ν·Q |
| (II) | η·Q = ν·Q ⇒ η = ν |
| (III) | Q = 1·Q |
Es wäre höchst unpraktisch, wenn für das Messen bzw. das Berechnen von Flächeninhalten Einheitsflächen von unterschiedlicher Form und Größe verwendet würden. Deswegen ist als Einheit für den Flächeninhalt der Quadratmeter festgelegt. Dieser ist definiert als Inhalt der Fläche eines Quadrats mit der Seitenlänge 1 Meter. Der Quadratmeter (Einheitenzeichen: m2) ist also von der Längeneinheit Meter (Einheitenzeichen: m) abgeleitet. Der Meter ist eine der sieben Basiseinheiten des Internationalen Einheitensystems (Système International d’Unités; Abkürzung: SI).
Der Meter
Die Bezeichnung „Meter“ (französisch: mètre) wurde auf Vorschlag des Mathematikers und Seemanns Jean-Charles de Borda am 1. August 1793 vom Nationalkonvent (Convention nationale) während der Französischen Revolution per Gesetz eingeführt. 1 Meter wurde damals definiert als zehn-millionster Teil des durch die Sternwarte von Paris gehenden, vom Nordpol bis zum Äquator reichenden Erdquadranten. Auf Grundlage geodätischer Messungen wurde im Jahr 1799 das sogenannte Urmeter als Endmaß aus Platiniridium angefertigt. 1889 wurde dieses Urmaß vom internationalen Meterprototyp abgelöst, einem Metallstab mit x-förmigem Querschnitt. Der Meter war durch den Abstand der Mittelstriche zweier Strichgruppen auf diesem Stab repräsentiert, was auf der ersten Sitzung der internationalen Generalkonferenz für Maß und Gewicht (Conférence Générale des Poids et Mesures; Abkürzung: CGPM) bestätigt wurde. 1960 wurde der Meter neu definiert: als das 1 650 763,73-fache der Wellenlänge der von Atomen des Nuklids 86Kr bei einem bestimmten Übergang ausgesandten, sich im Vakuum ausbreitenden Strahlung.
Auf der 26. Sitzung der CGPM im Jahr 2018 wurde beschlossen, dass sieben definierende Naturkonstanten die Grundlage für die Definition der SI-Basiseinheiten (Sekunde, Meter, Kilogramm, Ampere, Kelvin, Mol, Candela) bilden sollen. Für den Meter sind danach zwei Naturkonstanten maßgebend: explizit die Lichtgeschwindigkeit (299 792 458 ms−1) und implizit die Hyperfeinübergangsfrequenz des Cäsiumatoms (9 192 631 770 Hz). Eine Sekunde ist gleich der Dauer von 9 192 631 770 Schwingungen der Strahlung, die der Energie des Übergangs zwischen den zwei Hyperfeinstrukturniveaus des ungestörten Grundzustands im 133Cs-Atom entspricht und ein Meter ist gleich der Strecke, die von Licht innerhalb des Bruchteils von 1299792458 einer Sekunde im Vakuum zurückgelegt wird.
Dezimale Teile und Vielfache von 1 m2
Flächeninhalte können im Hinblick auf ihre Größenordnung erheblich voneinander abweichen. Deswegen gibt es neben der Einheit Quadratmeter noch die folgenden gebräuchlichen Einheiten:
| Quadratkilometer | 1 km2 = 1 000 000 m2 |
| Hektar | 1 ha = 10 000 m2 |
| Ar | 1 a = 100 m2 |
| Quadratdezimeter | 1 dm2 = 0,01 m2 |
| Quadratzentimeter | 1 cm2 = 0,0001 m2 |
| Quadratmillimeter | 1 mm2 = 0,000 001 m2 |
Das Ar und der Hektar sind keine SI-konformen Einheiten, gleichwohl in Deutschland, Österreich und in der Schweiz (dort: Are und Hektare) gesetzlich zugelassene Einheiten, die in der Landwirtschaft und im Grundbuchwesen benutzt werden.
Anglo-amerikanische Einheiten
In den USA,im Vereinigten Königreich und anderen englischsprachigen Ländern werden Flächeninhalte oft in Quadratfuß (square foot) gemessen. Als Einheitenzeichen wird beispielsweise „sq. ft.“ verwendet. 1 sq. ft. ist definiert als Inhalt der Fläche eines Quadrats mit der Seitenlänge 1 Fuß (1 foot).
1 foot = 13 yard = 12 inches
Ein Fuß entspricht 30,48 cm.
Flächeninhalt als Produkt zweier Längen
Im vorigen Abschnitt (Rechteckflächen) wurde gezeigt, dass die Formel zur Berechnung des Flächeninhalts A eines Rechtecks,
A = α·β Q ,
immer gilt, das heißt: die Längenmaßzahlen α und β dürfen irgendwelche reellen Zahlen sein. Unter Verwendung des Quadratmeters als Flächeneinheit lautet diese Formel
A = α·β m2 .
In Worten: Wenn die Länge a der einen Seite eines Rechtecks α-mal größer ist als 1 m (a = α m) und die Länge b der anderen Seite dieses Rechtecks β-mal größer ist als 1 m (b = β m), so ist der Inhalt der Rechteckfläche α·β-mal größer als 1 m2.
A kann als Produkt der Seitenlängen a und b geschrieben werden:
A = a·b.
Eine der Rechteckseiten wird „Breite“ genannt, die jeweils andere ist die „Höhe“ des Rechtecks.
Die Maßzahlen von a bzw. b dürfen hierbei nur dann ohne Weiteres miteinander multipliziert werden, wenn diese sich auf dieselbe Längeneinheit beziehen! Zwei Rechenbeispiele:
A1 = 0,7 m · 0,3 m = 0,21 m2.
A2 = 0,01 m · 70 cm = 0,01 m · 0,7 m = 0,007 m2.
Wenn in den folgenden Abschnitten von Polygonen die Rede ist, sollen damit stets einfache Polygone gemeint sein. Bei einem solchen Polygon sind die Ecken paarweise verschieden voneinander, kein Eckpunkt des Polygons gehört zu einer seiner Seiten und jeweils zwei Seiten haben keinen Punkt gemeinsam. Einfache Polygone werden auch Jordan-Polygone oder (vor allem dann, wenn sie übersichtlich genug ausschauen) auch n-Ecke genannt (n ≥ 3). Die Seiten eines Polygons bilden zusammen mit den Eckpunkten seinen Rand.
Diese Polygone sind Teil der Ebene. In „der Ebene“ dieses Kapitels (verstanden als Menge aller zu ihr gehörenden Punkte und mit dem Symbol „ε“ bezeichnet) sind die Gesetze der euklidischen Geometrie gültig, wobei nach X87 jeder Punkt P(xP; yP) der Ebene mit dem geordneten Paar seiner Koordinaten identifiziert werden kann (vgl.: rechtwinklige Koordinaten). Zueinander kongruente Strecken sind gleichlang, zueinander kongruente Winkel besitzen dieselbe Weite.
An dieser Stelle sei bemerkt, dass in diesem Kapitel Strecken mit Normalbuchstaben und ihre Längen mit entsprechenden kursiven Buchstaben bezeichnet werden. Demnach sind beispielsweise a und b die Längen der Strecken a bzw. b.
Jedes Polygon p zerlegt die Ebene ε in drei paarweise disjunkte und nichtleere Teilmengen (→ Beweis): sein Inneres in(p) („inner of polygon“), seinen Rand bd(p) („border of polygon“) und sein Äußeres ou(p) („outer of polygon“). Liegt ein Punkt im Innern eines Polygons p, so ist er ein innerer Punkt, liegt er im Äußeren, so ist er ein äußerer Punkt von p. Gehört ein Punkt zum Rand von p, so heißt dieser Punkt Randpunkt von p.
Das Innere und der Rand eines Polygons p bilden zusammen seine Fläche p:
p =def
in(p) ∪ bd(p).
Das Gleiche gilt offensichtlich für jeden Kreis: das Innere in(k) eines Kreises k besteht aus allen Punkten, deren Abstand zum Kreismittelpunkt kleiner als der Kreisradius ist; der Rand bd(k) entspricht der Kreislinie; zum Äußeren ou(k) gehören alle Punkte, deren Abstand zum Kreismittelpunkt größer als der Kreisradius ist. Außerdem gilt für die Kreisfläche k:
k = in(k) ∪ bd(k).
Da ein einfaches Polygon nur endlich viele Ecken besitzt, ist es beschränkt. Das heißt, es existiert für jedes Polygon ein Kreis, so dass alle Eckpunkte und damit alle inneren Punkte sowie alle Randpunkte des Polygons innerhalb der Kreislinie liegen. Mit anderen Worten: Der Abstand jedes Eckpunktes, jedes inneren Punktes und jedes Randpunktes zum Kreismittelpunkt ist − unter der Voraussetzung, dass der Kreis passend gewählt wurde − kleiner als der Kreisradius. Zu jedem Polygon p gibt es also einen Kreis k, so dass
p ⊂ k.
Die Zerlegung der Ebene ε durch ein (beliebig gewähltes) Dreieck ABC ist (ohne Verwendung kartesischer Koordinaten) leicht einzusehen. Mit jA sei das Innere des Winkels ∠A bezeichnet. Für jB und jC wird Entsprechendes vereinbart. Dann kann das Innere des Dreiecks ABC durch
in(ABC) =def jA ∩ jB ∩ jC
definiert werden; für seinen Rand gilt
bd(ABC) =
AB ∪ BC ∪ CA ∪ {A} ∪ {B} ∪ {C}.

Aufgrund des Crossbar-Theorems ist entscheidbar, ob ein Punkt im Innern eines Dreiecks ABC liegt oder nicht. A, B und C sowie alle Punkte, die zwischen A und B, B und C bzw. C und A liegen, gehören zum Dreiecksrand. Jeder Punkt, der weder im Dreiecksinnern noch auf dem Dreiecksrand liegt, gehört zum Äußeren des Dreiecks.
In entsprechender Weise kann im Fall konvexer n-Ecke auch für n ≥ 4 argumentiert werden. Die Aussage, dass jedes beliebige Polygon p die Ebene in drei paarweise disjunkte und nichtleere Teilmengen in(p), bd(p) und ou(p) zerlegt, muss (und kann) bewiesen werden. Hierzu werden vorab einige Definitionen getroffen:
Seien X und Y zwei verschiedene Eckpunkte eines Polygons p. Dann heißt die Strecke XY Diagonale von p. Gehören alle Punkte zwischen X und Y zum Inneren von p, so ist XY eine innere Diagonale von p.
Zwei Dreiecke überlappen sich, wenn sie mindestens einen inneren Punkt gemeinsam haben.
Wird ein Polygon p durch m Dreiecke d1, d2, ..., dm so unterteilt, dass (i) jeder Eckpunkt dieser Dreiecke auch Eckpunkt von p ist, (ii) jede Seite dieser Dreiecke auch Seite oder innere Diagonale von p ist, (iii) jeder innere Punkt von p entweder auf einer dieser inneren Diagonalen liegt oder innerer Punkt von genau einem der m Teildreiecke ist, so sagt man kurz: „p wird durch die m Teildreiecke trianguliert“.
Aufgrund der Eigenschaft (iii) überlappt sich kein Teildreieck eines triangulierten Polygons mit einem der jeweils anderen Teildreiecke.
Sei M eine Teilmenge der Ebene. M heißt offen, wenn es zu jedem Punkt P ∈∈ M eine positive reelle Zahl r gibt, so dass das Innere des Kreises mit dem Radius r ganz in M enthalten ist. Eine offene Menge M heißt zusammenhängend, wenn es für je zwei Punkte P und Q mit P,Q ∈∈ M einen Streckenzug von P nach Q gibt, der ganz in M liegt. Eine Teilmenge der Ebene heißt Gebiet, wenn sie offen und zusammenhängend ist.
![]() A1
A1
Sei p ein beliebig gewähltes einfaches Polygon mit n Ecken.
(i) Die Ebene wird durch p in genau drei Mengen
zerlegt. Eine dieser Teilmengen ist der Rand von p.
(ii) Die vom Rand von p verschiedenen Teilmengen sind Gebiete, von denen eines beschränkt und das andere nicht
beschränkt ist.
(iii) Ist PQ eine Strecke, die von genau einer der
Polygonseiten geschnitten wird, so gehört einer der beiden Endpunkte von PQ zu dem einen Gebiet
und der andere Endpunkt zum jeweils anderen Gebiet.
(iv) p ist triangulierbar.
Beweis (mit vollständiger Induktion über n):
Induktionsanfang (für n = 3):
Die Zerlegung der Ebene durch ein Dreieck ABC
wurde bereits oben nachgewiesen. Das Innere in(ABC)
ist stets beschränkt; das Äußere ou(ABC) ist offensichtlich nicht beschränkt. Auch (iii)
ist erfüllt (vgl. hierzu X7 und die
Definition eines Winkels).
Die Triangulation jedes Dreiecks besteht trivialerweise aus sich selbst.
Induktionsvoraussetzung:
Es sei angenommen, dass die Aussagen (i) bis (iv) für jedes Polygon, das
nicht mehr als m Eckpunkte besitzt, wahr sind.
Induktionsschluss:
Gegeben sei in einer kartesischen
Ebene ein beliebig gewähltes Polygon p mit m+1 Eckpunkten. Der (bzw. ein)
Eckpunkt mit minimaler x-Koordinate sei mit S0(x0; y0)
und alle weiteren Eckpunkte fortlaufend mit S1, S2, ...
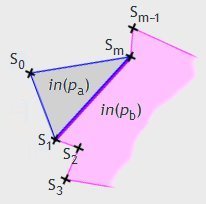
bezeichnet. Dann gibt es für das Dreieck S1SmS0 zwei Möglichkeiten:
Fall 1. S1Sm ist eine innere Diagonale von p. Dann sind für die Polygone pa[S1SmS0S1] (alias dem Dreieck S1SmS0) und pb[S1S2...Sm−1SmS1] die Aussagen (i) bis (iv) gültig und beide haben (nur) die Seite s =def SmS1 gemeinsam.
Fall 2. Im Innern von S1SmS0 oder zwischen S1 und Sm befinden sich Eckpunkte von p. Sei unter diesen Eckpunkten St derjenige (bzw. ein) Punkt, dessen Abstand zu S0 minimal ist. Dann sind für die Polygone pa[S0StSt+1...Sm−1SmS0] und pb[S0S1S2...St−1StS0] die Aussagen (i) bis (iv) gültig und beide haben (nur) die Seite s =def S0St gemeinsam.
(1)
In beiden Fällen ist
j =def in(pa) ∪ in(pb) ∪ s
ein Gebiet, wobei zu beachten ist, dass die Endpunkte von s (Sm und S1 im Fall 1 bzw. S0 und St im Fall 2) nicht zu s gehören. Da in(pa), in(pb) sowie s beschränkt sind, ist auch j beschränkt.
(2)
Sei nun s* die Menge, die entsteht, wenn die Endpunkte von s
zu s hinzufügt werden. Dann ist nach Konstruktion rd(pb)\s*
weder eine Teilmenge von rd(pa) noch von in(pa).
Demzufolge gilt in beiden Fällen
rd(pb)\s* ⊂ ou(pa)
und damit auch in(pb)\s* ⊂ ou(pa).
Da in(pa) und ou(pa)
nach Induktionsvoraussetzung disjunkte Mengen sind, folgt
in(pa) ⊂ ou(pb)
und hieraus, dass in(pa) und in(pb) keine Punkte gemeinsam haben. Sowohl pa als auch pb sind triangulierbar, und zwar wegen des Vorstehenden derart, dass genau ein Dreieck der einen und genau ein Dreieck der anderen Triangulation eine gemeinsame Seite haben, nämlich s. Das bedeutet, dass p trianguliert wird.
(3)
Die durch
o =def ou(pa) ∩ ou(pb)
definierte Menge o ist als Durchschnitt zweier Gebiete wieder ein Gebiet. o ist unbeschränkt, denn sowohl zu ou(pa) als auch zu ou(pb) gehören alle Punkte der Ebene, sofern diese nur einen genügend großen Abstand zum Rand von p haben.
(4)
Für den Rand von p gilt
rd(p) = (rd(pa) ∪ rd(pb))\ s.
Unter Beachtung der Rechengesetze bezüglich
∪ und ∩ weist man unschwer nach, dass
o, j und rd(p) einerseits paarweise disjunkt sind und andererseits zur Vereinigungsmenge
o ∪ j ∪ rd(p)
sämtliche Punkte der Ebene gehören.
(5)
Sei PQ eine Strecke, die von genau einer
der Seiten von p geschnitten wird. Diese Seite gehört dann
entweder zu pa oder zu pb.
Sei etwa angenommen, dass PQ eine Seite von pa schneidet
und P ∈∈ in(pa).
Nach Induktionsvoraussetzung ist dann Q ∈∈ ou(pa).
Wegen in(pa) ⊂ j
gilt auch P ∈∈ j.
Andererseits schneidet PQ keine Seite von pb,
wonach wegen in(pa) ⊂ ou(pb)
neben P auch Q zu ou(pb) gehört.
Es folgt Q ∈∈ o,
was für (iii) noch zu zeigen war.
Die Bezeichnungen für die Gebiete j und o wurden oben bereits eingeführt: o = ou(p) ist das Äußere von p, j = in(p) das Innere von p.
Die Verallgemeinerung der Aussagen A1(i)-(ii) auf geschlossene (auch nicht-polygonale) Jordan-Kurven wurde erstmalig 1905 vom US-amerikanischen Mathematiker Oswald Veblen korrekt bewiesen. Anschaulich formuliert: In der euklidischen Ebene wird das Komplement jeder geschlossenen, stetigen und schnittpunktfreien Kurve in genau zwei disjunkte Gebiete zerlegt, von denen eines beschränkt und das andere unbeschränkt ist.
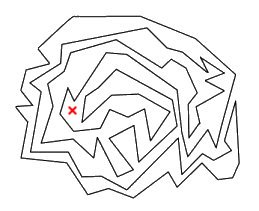
Was mit dem Inneren eines Polygons gemeint ist, mag anschaulich klar sein. Man benötigt allerdings (unabhängig von der Anschauung) ein Kriterium, mit dem eindeutig entscheidbar ist, ob ein beliebig gewählter Punkt der Ebene ein innerer Punkt eines Polygons ist oder eben nicht ist. Ist der rot markierte Punkt im nachfolgenden Diagramm ein innerer Punkt oder nicht?
![]() A2
A2
Sei p ein beliebig gewähltes einfaches Polygon und P ein Punkt der Ebene. Dann lässt sich eindeutig feststellen,
ob P im Innern, im Äußeren oder auf dem Rand von p liegt.
Beweis:
Gegeben seien ein beliebig gewähltes Polygon p und
irgendein Punkt P der Ebene.
(1)
Unter Benutzung eines
kartesischen Koordinatensystems
kann man nachrechnen, ob P auf dem Rand von p liegt oder nicht.
(2)
Seien nun P und ferner Q Punkte, die nicht zum Rand
dieses Polygons gehören. Ist dann PQ eine Strecke, die von genau einer der Polygonseiten
geschnitten wird, so ist nach A1(iv) stets einer der beiden Endpunkte
von PQ ein innerer, der jeweils andere ein äußerer Punkt.
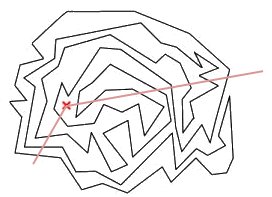
Sei h eine von P ausgehende, nicht durch Eckpunkte von p laufende, aber ansonsten beliebig gewählte Halbgerade. Sei ferner ein Kreis k so gewählt, dass alle Eckpunkte innerhalb der Kreislinie von k liegen. Der Schnittpunkt von h und k sei mit S bezeichnet. Dann ist aufgrund des eben Gesagten P genau dann ein innerer Punkt von p, wenn die Anzahl der Schnittpunkte zwischen der Strecke PS und irgendwelchen Seiten von p ungerade ist. Anderenfalls handelt es sich um einen äußeren Punkt.
Beispielsweise ist der rot markierte Punkt im obigen Diagramm ein äußerer Punkt des Polygons:
Gemäß des Vorschlags von Gary Hosler Meisters wird das Folgende vereinbart:
Drei unmittelbar aufeinander folgende Eckpunkte Si−1, Si, Si+1 eines einfachen Polygons p bilden mit dem Dreieck Si−1SiSi+1 genau dann ein Ohr am Eckpunkt Si, wenn die Strecke Si−1Si+1 eine innere Diagonale von p ist.
![]() A3
(Zwei-Ohren-Theorem)
A3
(Zwei-Ohren-Theorem)
Jedes einfache Polygon mit mehr als drei Eckpunkten hat mindestens zwei
sich nicht überlappende Ohren.
Beweis (mit vollständiger Induktion):
(vgl. mit G.H. Meisters: POLYGONS HAVE EARS)
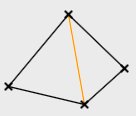
Induktionsanfang (für n = 4):
Ein Viereck hat entweder zwei innere
Diagonalen oder genau eine innere Diagonale. In beiden Fällen ist die behauptete Aussage erfüllt.
Induktionsvoraussetzung:
Es sei angenommen, dass die behauptete Aussage für jedes Polygon, das
mehr als drei, aber nicht mehr als m Eckpunkte besitzt, wahr ist.
Induktionsschluss:
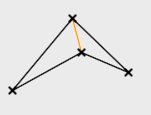
Sei nun ein Polygon p mit m+1 Eckpunkten beliebig gewählt. Dann hat p stets einen Eckpunkt S,
der zusammen mit seinen unmittelbar benachbarten Eckpunkten S* und S** die Eigenschaft hat, dass der
Durchschnitt vom Inneren des Winkels ∠S*SS** und dem Inneren des Polygons
in(p) nicht leer ist. Sei ein solcher Eckpunkt mit S0
und alle weiteren Eckpunkte fortlaufend mit S1, S2,
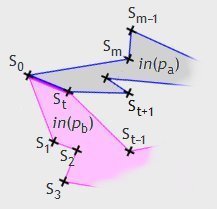
... bezeichnet. Dann gibt es für das Dreieck S1SmS0 zwei Möglichkeiten:
Fall 1. S1Sm ist eine innere Diagonale von p. Dann hat p ein Ohr an S0. Wird dieses Ohr entfernt, so erhält man ein Polygon p* mit m Eckpunkten, das − sofern p* kein Dreieck ist − gemäß Induktionsvoraussetzung zwei sich nicht überlappende Ohren besitzt. Es ist ausgeschlossen, dass diese zwei Ohren an S1 bzw. an Sm sitzen, denn säßen sie dort, würden sie sich überlappen. p* hat also mindestens ein Ohr an einem sowohl von S1 als auch von Sm verschiedenen Eckpunkt. Dieses Ohr zusammen mit dem Ohr S1SmS0 sind die gesuchten zwei sich nicht überlappenden Ohren von p.
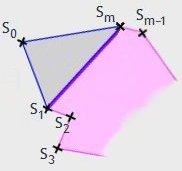
Fall 2. Im Innern von S1SmS0 oder zwischen S1 und Sm befinden sich Eckpunkte von p. Unter diesen Eckpunkten sei St derjenige (bzw. ein) Punkt, dessen Abstand zu S0 minimal ist. Dann ist die Strecke S0St eine innere Diagonale von p. p wird von dieser Strecke in die zwei Polygone pa[S0StSt+1...Sm−1SmS0] und pb[S0S1S2...St−1StS0] zerteilt, wobei beide Teilpolygone (nur) die Seite S0St gemeinsam haben.
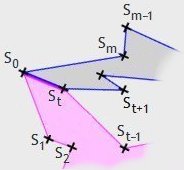
Weil m+1 größer oder gleich 5 ist, kann entweder pa oder pb kein Dreieck sein.
Sei ohne Beschränkung der Allgemeinheit etwa pa kein Dreieck. Dann gibt es für das Polygon
pb zwei Möglichkeiten:
(1) pb ist ein Dreieck. In diesem Fall gilt t = 2 und
S0S1S2 ist ein Ohr von p. Das Polygon pa hat dann gemäß
Induktionsvoraussetzung zwei sich nicht überlappende Ohren. Mindestens eines von beiden Ohren befindet sich
an einem sowohl von S0 als auch von S2
verschiedenen Eckpunkt. Dieses Ohr zusammen mit dem Ohr S0S1S2
sind die gesuchten zwei sich nicht überlappenden Ohren von p.
(2) pb ist kein Dreieck. Dann haben beide Teilpolygone pa und
pb jeweils mindestens ein Ohr, das sich weder an S0 noch an St befindet.
Hieraus folgt auch in diesem Fall die behauptete Aussage.
Das Zwei-Ohren-Theorem besagt, dass man von jedem einfachen Polygon mit mehr als drei Eckpunkten solange sukzessiv jeweils ein Ohr (respektive ein Dreieck) abschneiden kann, bis schließlich nur noch ein Dreieck übrig bleibt.
Es sei an dieser Stelle erinnert, dass in diesem Kapitel mit dem Wort Polygon immer ein einfaches Polygon gemeint ist.
Eine Polygonfläche ist eine Teilmenge der Ebene, die sich durch eine endliche Anzahl sich nicht überlappender Dreiecksflächen beschreiben lässt.
Die Fläche p eines Polygons p ist stets eine Polygonfläche, denn jedes Polygon ist triangulierbar.
Sowohl der Durchschnitt als auch die Vereinigung zweier Polygonflächen ist eine Polygonfläche. Außerdem ist das Komplement einer Polygonfläche bezüglich einer anderen Polygonfläche ebenfalls eine Polygonfläche.
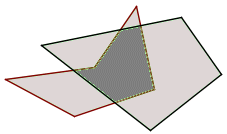
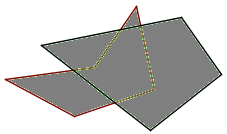
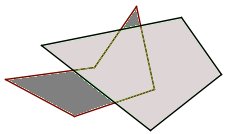
Ist p = n⋃i = 1di eine Polygonfläche mit paarweise sich nicht überlappenden Dreiecksflächen d1, d2, ..., dn, so heißt die Menge
ζ(p) = { d1, d2, ..., dn }
Zerlegung von p. (In verständlicher Weise spricht man genauso gut von der Zerlegung des Polygons p in die Dreiecke d1, d2,..., dn.)
Gegeben seien zwei Zerlegungen ζ(p) und ζ*(p) einer Polygonfläche p. Dann heißt ζ(p) feiner als ζ*(p), wenn zu ζ(p) mehr Dreiecksflächen gehören als zu ζ*(p) und wenn es zu jedem di ∈∈ ζ(p) ein d*j ∈∈ ζ(p*) gibt mit di ⊆ d*j. ζ*(p) heißt dann gröber als ζ(p).
Seien d1, d2, ..., dn sich paarweise nicht überlappende Dreiecksflächen und d*1, d*2, ..., d*m Dreiecksflächen, für die das Gleiche gilt. Dann überlappen sich die zwei Polygonflächen n⋃i = 1di und m⋃j = 1d*j genau dann nicht, wenn sich für jede der Dreiecksflächen di unter den Dreiecksflächen d*j keine findet, so dass sich di und d*j überlappen.
Sind p1 und p2 zwei sich nicht überlappende Polygonflächen
und gilt p = p1 ∪ p2,
so sagt man: „p ist in p1 und p2
zerlegt“.
Um die Inhalte von Polygonflächen messen zu können, wird eine Abbildung α benötigt, die in eindeutiger Weise jedem Polygon bzw. dessen Fläche eine positive reelle Zahl μ zuordnet. Die Idee besteht darin, dass die Maßzahl μ den Inhalt der jeweiligen Fläche angibt, und zwar relativ zum Inhalt der Einheitsfläche, der die Maßzahl 1 zugeordnet wird.

Sei p eine beliebige Polygonfläche und ζ(p) eine Zerlegung mit den n Dreiecksflächen d1, d2, ..., dn. Unter der Voraussetzung, dass α(d) für jede Dreiecksfläche d eindeutig bestimmt werden kann (siehe hierzu A4), liegt es auf der Hand, das Flächenmaß von p durch
α(p) = n∑i = 1α(di)
zu definieren. Hierzu muss allerdings vorher noch nachgewiesen werden, dass α(p) unabhängig von der gewählten Zerlegung ζ(p) eindeutig bestimmt ist (siehe A6 und A7).
Sei mit ℱ die Menge aller Polygonflächen bezeichnet. Dann werden für das Flächenmaß
α: ℱ → [0, ∞]
die folgenden zwei − anschaulich selbstverständlichen − Eigenschaften axiomatisch gefordert:
(F1) Sind je zwei Dreiecke ABC und DEF kongruent zueinander, so gilt
α(ABC) = α(DEF).
(F2) Ist p eine in die Teilflächen p1 und p2 zerlegte Polygonfläche, so gilt
α(p) = α(p1) + α(p2).
Die im Abschnitt Rechteckflächen hergeleitete Formel zur Berechnung des Inhalts rechteckiger Flächen ist Vorlage für die dritte Eigenschaft der Abbildung α:
(F3) Sei ABCD ein beliebiges Rechteck. Die Länge der Strecke AB sei mit a, diejenige von BC mit b bezeichnet. Dann gilt
α(ABCD) = a·b.
![]() A4
A4
Gegeben sei ein beliebiges Dreieck ABC. Sei eine der drei Seiten von ABC beliebig ausgewählt,
mit „Grundseite“ benannt und mit g bezeichnet; sei ferner h die Höhe auf g. Ist g die Länge von g und h die Länge von h,
dann gilt
α(ABC) = 12·g·h.
Beweis:
(1)
Jedes Dreieck hat mindestens zwei spitze Innenwinkel. (Die Annahme, es gäbe ein Dreieck mit nur einem spitzen Innenwinkel,
würde sofort zu einem Widerspruch zum Satz von der Winkelsumme im Dreieck führen.)
Gegeben sei nun ein beliebiges Dreieck ABC. Ohne Beschränkung der Allgemeinheit seien ∠A
und ∠B spitze Winkel. Dann liegt die
Höhe hc im Innern von ∠C und
ihr Fußpunkt F zwischen A und B. Die Länge von hc sei mit hc bezeichnet.
Sei q die Länge der Strecke AF und p diejenige von FB. Der Punkt D, dessen Abstand zu A gleich h und zu C gleich q ist, ist eindeutig bestimmt. Das Gleiche gilt für den Punkt E mit |EB| = h und |CE| = p.
Mit dem Kongruenzsatz sss folgt AFC ≅ CDA bzw. BFC ≅ CEB und hieraus α(AFC) = α(CDA) sowie α(BFC) = α(CEB) wegen (F1).
A, B, E und D sind Eckpunkte eines Rechtecks mit den Seitenlängen c und hc. Also folgt schließlich mit (F2) und (F3)
A = 12·c·hc.
(2)
Gegeben sei ein beliebiges Dreieck mit denselben Bezeichnungen wie unter (1). Sei zudem hb die Höhe
auf b und G ihr Fußpunkt. Dann sind nach dem Ähnlichkeitssatz X63(i) die
Dreiecke AFC und AGB ähnlich zueinander. Demzufolge gilt
hbc = hcb
und damit auch
c·hc = b·hb.
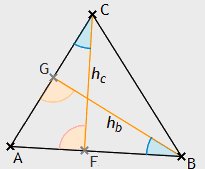

(3)
Auf analoge Weise folgt
c·hc = a·ha.
Aus (F2) folgt mittels vollständiger Induktion ohne Weiteres der folgende Satz:
![]() A5
A5
Sei pζ eine mittels ζ(p) = { d1, d2,
..., dn } zerlegte Polygonfläche, so gilt
α(pζ ) = α(n⋃i = 1di) = n∑i = 1α(di).
![]() A6
A6
Gegeben sei ein beliebiges Dreieck ABC. Dann gilt für jede Zerlegung
ζ(ABC) = { d1,
..., dn }
n∑i = 1α(di) = α(ABC).
Beweis:
Sei ABC ein Dreieck mit einer beliebigen Zerlegung in n Teildreiecke
d1, d2,
..., dn. Sei ohne Beschränkung der Allgemeinheit angenommen, dass
∠A und ∠B spitze Winkel sind. Dann gibt es nach
X18 zu jedem der k Eckpunkte
Pi (i = 1..k) im Innern von ABC bzw. auf AB eine Halbgerade CPi>,
die sich mit AB in einem Punkt, etwa in Si, schneidet.

Nach Teilung jedes der durch die Halbgeraden entstehenden Teilvierecke in jeweils zwei neue Teildreiecke erhält man schließlich eine Zerlegung jeder i-ten Dreiecksfläche di in m(i) kleine Teildreiecke d*ir und es gilt nach A5
n∑i = 1α(di)
= n∑i = 1 m(i)∑r = 1α(d*ir)
= N∑j = 1α(d*j)
bei passender Indizierung und N = n∑i = 1m(i). Man benenne nun den Punkt A um in S0 sowie den Punkt B in Sk+1. Dann sei die jeweilige Fläche des Dreiecks SiSi+1C mit d’i und die Länge der Strecke SiSi+1 mit si bezeichnet.
Nach Konstruktion geht keine der Halbgeraden OPi> durch das Innere irgendeines der Dreiecke d*j. Also gilt
N∑j = 1α(d*j)
= k∑i = 1α(d’i)
= k∑i = 112·si·hc
= 12·c·hc
= α(ABC), was zu beweisen war.
![]() A7
A7
Gegeben sei ein beliebiges Polygon p mit zwei verschiedenen Zerlegungen ζ(p) = { d1,
..., dn }
und ζ*(p) = { d*1,
..., d*m }.
Dann gilt
n∑i = 1α(di) = m∑i = 1α(d*i).
Beweis:
Gegeben sei eine beliebige Polygonfläche
p mit zwei verschiedenen Zerlegungen
ζ(p) = { d1, d2, ..., dn } und ζ*(p) = { d*1, d*2, ..., d*m }.
Mittels der Kanten der Dreiecke di (i = 1..n) gemeinsam mit den Kanten der Dreiecke dj (j = 1..m) kann eine neue Zerlegung
ζ’(p) = { d’1, d’2, ..., d’N }
definiert werden und zwar dergestalt, dass sowohl jede Dreiecksfläche di als auch jede Dreiecksfläche d*j mit Dreiecken zerlegt ist, die zu ζ’(p) gehören.

Mit anderen Worten: ζ’(p) ist feiner als ζ(p) und zudem feiner als ζ*(p). Mit (F2) und A6 folgt
n∑i = 1α(di) = N∑l = 1α(d’l) = m∑j = 1α(d*j).
Nach A7 kann nunmehr folgende Definition getroffen werden:
Sei p eine beliebige Polygonfläche und ζ(p) eine Zerlegung mit den n Dreiecksflächen d1, d2, ..., dn. Dann ist
α(p) =def n∑i = 1α(di).
Beispielsweise lässt sich ein Parallelogramm (das ist ein Viereck, bei dem die jeweils gegenüberliegenden Seiten parallel zueinander sind) in zwei zueinander kongruente Dreiecke zerlegen. Wird im Parallelogramm ABCD die Länge der Seite AB mit a und die Länge der Lotstrecke von D auf AB mit ha bezeichnet, so folgt
α(ABCD) = a·ha.
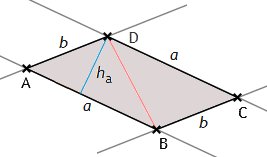
Nebenbei sei bemerkt, welche Rolle das Parallelogramm in der Vektorrechnung spielt: Bildet man das Kreuzprodukt zweier Vektoren a und b, so erhält man als Ergebnis den Vektor axb, dessen Länge der Fläche des von a und b aufgespannten Parallelogramms entspricht.
![Rechtssystem [a, b, axb]](images/axb.gif)
Eine bijektive Abbildung φ: ε → ε heißt Isometrie, wenn für alle Punkte P,Q ∈∈ ε
PQ ≡ φ(P)φ(Q)
gilt, das heißt, wenn jede Strecke PQ ⊂ ε kongruent ist zur Strecke φ(P)φ(Q).
Die eine Isometrie φ charakterisierende Gleichung PQ ≡ φ(P)φ(Q) ist nach X66 äquivalent zu ℓ(PQ) = ℓ(φ(P)φ(Q)) bzw. |PQ| = |φ(P)φ(Q)|. Eine Isometrie ist also stets längen- bzw. abstandstreu. (Der Begriff Isometrie stammt aus dem Griechischen: ισομετρική = von gleichem Maß.)
![]() A8
A8
Eine Isometrie ist stets geradentreu. Das heißt: Ist φ
eine Isometrie, so wird jede Gerade durch φ
auf eine Gerade abgebildet. Gilt für drei kollineare Punkte A,B,C ∈∈ ε, dass B ∈∈ AC,
so folgt φ(B) ∈∈ φ(A)φC).
Beweis:
Gegeben sei eine beliebige Gerade g ⊂ ε.
A und B seien zwei Punkte, die zu g gehören. φ
sei eine Isometrie mit A’ = φ(A) und
B’ = φ(B).
Sei ferner g’ diejenige Gerade, die durch A’ und B’ geht. Sei
schließlich C ein dritter, sowohl von A als auch von B verschiedener, aber
ansonsten beliebig gewählter Punkt auf g und C’ = φ(C).
Angenommen, C’ ∉∉ g’. Dann bilden A’, B’ und C’ ein Dreieck und es gilt − unter der Annahme, dass C zwischen A und B liegt − nach X34 und X48
|A’C’| + |C’B’| > |A’B’|.
Es folgt
|AC| + |CB| > |A’B’|
und damit wegen |AB| = |AC| + |CB| ein Widerspruch zu AB ≡ A’B’.
Liegt A zwischen B und C oder B zwischen A und C, so argumentiert man entsprechend.
![]() A9
A9
Eine Isometrie ist stets winkeltreu. Das heißt: Ist φ
eine Isometrie und sind die Punkte A,B,C ∈∈ ε
nicht kollinear, so sind die Winkel
∠ABC und ∠φ(A)φ(B)φ(C)
zueinander kongruent.
Beweis:
Seien A,B,C ∈∈ ε
nicht kollinear, φ eine
Isometrie mit A’ = φ(A),
B’ = φ(B) und
C’ = φ(C).
Dann gilt AB ≡ A’B’, BC ≡ B’C’
bzw. CA ≡ C’A’ und mit dem Kongruenzsatz
sss folgt unmittelbar die Behauptung.
![]() A10
A10
Gegeben seien eine Gerade g ⊂ ε
und zwei beliebig gewählte Punkte P,Q ∈∈ ε.
Ist φ eine Isometrie, so liegen
P und Q genau dann auf derselben Seite von g, wenn φ(P)
und φ(Q) auf derselben Seite
von φ(g) liegen.
Demnach liegen P und Q genau dann auf verschiedenen Seiten von g, wenn φ(P) und φ(Q) auf verschiedenen Seiten von φ(g) liegen.
Beweis von A10:
„⇒“: Gegeben seien eine Gerade
g ⊂ ε
und zwei Punkte P,Q ∈∈ ε,
die auf derselben Seite von g liegen. Sei ferner φ eine Isometrie mit
P’ = φ(P) und
Q’ = φ(Q).
Angenommen, P’ und Q’ liegen unter diesen Voraussetzungen auf verschiedenen Seiten von
φ(g). Dann gibt es einen Punkt Z zwischen P’ und Q’ mit
Z ∈∈ φ(g).
Mit A8 folgt, dass das Urbild von Z (also ein Punkt auf g) zwischen
P und Q liegt. Somit liegen P und Q auf verschiedenen Seiten von g im Widerspruch zur Voraussetzung.
„⇐“: Da φ bijektiv ist, existiert zu φ die Umkehrabbildung φ−1. Mit P’ = φ(P) und Q’ = φ(Q) hat man P = φ−1(P’) und Q = φ−1(Q’). Also folgt P’Q’ ≡ φ−1(P’)φ−1(Q’), wonach φ−1 ebenso wie φ eine Isometrie ist.
Setzt man nun voraus, dass P’ und Q’ auf derselben Seite von φ(g) liegen, führt die Annahme, dass P und Q auf verschiedenen Seiten von g liegen, in gleicher Weise wie oben zu einem Widerspruch.
![]() A11
A11
Sind ABC und A’B’C’ zwei zueinander kongruente Dreiecke, so gibt es genau eine Isometrie
φ mit
φ(ABC) = A’B’C’.
Beweis:
Gegeben sei ein beliebiges Dreieck ABC und ein zu diesem
Dreieck kongruentes Dreieck A’B’C’. Die Gerade durch die Punkte A und B
sei mit g, diejenige durch A’ und B’ mit g’ bezeichnet.
(1) zu zeigen: die Existenz einer Abbildung φ
mit der geforderten Eigenschaft.
Setzt man
φ(A) =def A’, φ(B) =def B’, φ(C) =def C’,
so folgt wegen der Kongruenz beider Dreiecke AB ≡ φ(A)φ(B), BC ≡ φ(B)φ(C) und CA ≡ φ(C)φ(A).
Sei nun D ein von A, B und C verschiedener, aber ansonsten beliebiger Punkt.
Fall 1: D ∈∈ g.
In diesem Fall wähle man den Punkt D’ ∈∈ g’
so, dass DB ≡ D’φ(B)
gilt und die gegenseitige Lage von D’, A’ bzw. B’ der gegenseitigen Lage
von D, A bzw. B entspricht. Dann ist D’ gemäß Axiom III.1
eindeutig bestimmt.
Nach X9 bzw. X10 gilt dann auch
DB ≡ D’φ(B)
und wegen des Kongruenzsatzes sws
zudem DC ≡ D’φ(C).
Fall 2: D ∉∉ g.
Man trage in diesem Fall gemäß III.4
den Winkel ∠ABD bei B’ an der Halbgeraden B’A’> an, und zwar auf der
Seite von g’, auf welcher C’ liegt, falls D und C auf derselben Seite von g liegen, anderenfalls auf der
anderen Seite von g’. Auf dem so konstruierten Schenkel gibt es (wiederum nach III.1)
einen eindeutig festgelegten Punkt D’ mit AD ≡ φ(A)D’.
Mittels sws, angewandt auf die Dreiecke ABD und A’B’D’, folgt BD ≡ φ(B)D’,
und, angewandt auf die Dreiecke BCD und B’C’D’, folgt unter Beachtung von
X20 auch CD ≡ φ(C)D’.
In beiden Fällen definiere man φ(D) =def D’.
Für jeden weiteren Punkt E ∈∈ ε neben A, B, C und D kann auf analoge Art wie eben E’ konstruiert werden. Mittels sws, angewandt auf die Dreiecke BED und B’E’D’, folgt dann (abermals unter Beachtung von X20) ED ≡ φ(E)D’.
Wird mit E’ der jeweilige nach obiger Konstruktion zu E gehörende Punkt bezeichnet, ist mit φ(E) =def E’ die Abbildung φ auf ganz ε definiert und wegen der Transitivität von ≡ folgt aus dem Vorstehenden, dass φ eine Isometrie ist.
(2) zu zeigen: die Eindeutigkeit von φ.
Angenommen, es gibt eine von φ
verschiedene Isometrie ψ mit ψ(ABC) = A’B’C’.
Dann existiert mindestens ein Punkt P mit φ(P) ǂ ψ(P).
P kann nicht auf g liegen, denn der nach (1), Fall 1 konstruierte
Punkt P’ ist stets eindeutig bestimmt. Demzufolge bilden A, B und P
ein Dreieck. Es gilt sowohl ABP ≅ φ(A)φ(B)φ(P)
als auch ABC ≅ ψ(A)ψ(B)ψ(P),
also folgt
φ(A)φ(B)φ(P) ≅ ψ(A)ψ(B)ψ(P).
Dann liegen φ(P) und ψ(P)
entweder auf derselben Seite von g’ (dann hat man mit φ(P) = ψ(P)
sofort einen Widerspruch zur Annahme) oder aber φ(P) und ψ(P) liegen auf
verschiedenen Seiten von g’, was aber nach A10 ausgeschlossen ist.
![]() A12
A12
Sei P ein Punkt im Innern eines beliebigen Dreiecks ABC.
Dann gibt es keinen weiteren Punkt Q mit
|PA| = |QA|, |PB| = |QB| und |PC| = |QC|.
Beweis:
Angenommen, es gibt einen von P verschiedenen Punkt Q mit
den angegebenen Eigenschaften. Dann sind die Dreiecke ABP und ABQ nach dem Kongruenzsatz
sss kongruent zueinander.
Wegen P ǂ Q treffen allerdings wenigstens zwei der folgenden Aussagen zu:
∠BAP ǂ ∠BAQ,
∠APB ǂ ∠AQB,
∠PBA ǂ ∠QBA.
Das ist ein Widerspruch.
Ist P ein Punkt im Innern eines Dreiecks ABC und ist A’B’C’ das zugehörige Bilddreieck unter einer Isometrie φ, dann folgt aus A12, dass der Bildpunkt φ(P) relativ zu A’, B’ bzw. C’ die gleiche Position hat wie sein Urbild P relativ zu A, B bzw. C.
Zwei Polygonflächen heißen zueinander kongruent, wenn sie durch eine Isometrie aufeinander abgebildet werden können.
Anschaulich formuliert: Kongruente Polygonflächen stimmen in Form und Größe überein. Sie sind also deckungsgleich.
Die Möglichkeit, mit einem geeignet definierten Flächenmaß α den Inhalt einer (Polygon)fläche zu bestimmen, setzt voraus, dass jeder Strecke eine gewisse Länge eindeutig zugeordnet werden kann, mit anderen Worten: dass man Streckenlängen messen kann. Für den Beweis der Messbarkeit aller Strecken wird das Archimedische Axiom benötigt (vgl. X47).
Es ist allerdings sinnvoll, auch ohne die Gültigkeit des Archimedischen Axioms vorauszusetzen, von dem Inhalt von Flächen zu sprechen:
Zwei Polygonflächen p und p* heißen zerlegungsgleich (in Zeichen: p z p*), wenn beide in eine endliche Anzahl von Dreiecksflächen zerlegt werden können, die paarweise zueinander kongruent sind.
Zwei Polygonflächen p und p* heißen inhaltsgleich (oder von gleichem Inhalt), wenn es möglich ist, ihnen zerlegungsgleiche Polygonflächen q bzw. q* überlappungsfrei hinzuzufügen, so dass
p ∪ q z p* ∪ q*
gilt.
Aus beiden Definitionen folgen unmittelbar die nachstehenden Sachverhalte:
![]() A13
A13
(i) Zwei Polygonflächen sind genau dann zerlegungsgleich, wenn man
beide in paarweise zueinander kongruente Teilpolygonflächen zerlegen kann.
(ii) Fügt man zerlegungsgleiche Polygonflächen p
und p* bzw. q und q*
überlappungsfrei zusammen, so sind auch p ∪ q und
p* ∪ q*
zerlegungsgleich. Fügt man inhaltsgleiche Polygonflächen p
und p* bzw. q und q* überlappungsfrei
zusammen, so sind auch p ∪ q und
p* ∪ q*
inhaltsgleich.
(iii) Zerlegungsgleiche Polygonflächen sind stets auch inhaltsgleich.
(iv) Gilt p z p* und
q z q* zusammen mit
q ⊂ p bzw.
q* ⊂ p*, so sind die reduzierten
Polygonflächen p \ q
und p* \ q*
inhaltsgleich.
![]() A14
A14
Für zwei zerlegungsgleiche Polygonflächen p und p* gilt α(p) = α(p*).
Beweis:
Die behauptete Aussage folgt aus der Definition der
Zerlegungsgleichheit zweier Polygonflächen in Verbindung mit A7 und der
Definition des Flächenmaßes für Polygone.
![]() A15
A15
Die Relation „z“ ist eine Äquivalenzrelation.
Beweis:
Die Relation „z“ ist selbstverständlich
reflexiv und symmetrisch. Zum Nachweis der Transitivität seien drei Polygonflächen p, p’
und p* gegeben. Unter der
Voraussetzung, dass p z p’
und p’ z p* gilt, lassen sich diese Polygonflächen wie folgt in Dreiecksflächen zerlegen:
p = n⋃i = 1di und p’ = n⋃i = 1d’i
mit
di ≅ d’i für i = 1, 2, ..., n
bzw.
p’ = m⋃j = 1ϑ’j und p* = m⋃j = 1ϑ*j
mit
ϑ’j ≅ ϑ*j für j = 1, 2, ..., m.
Jede Durchschnittsmenge
d’i ∩ ϑ’j
von sich überlappenden Dreiecksflächen d’i
und ϑ’j ist eine Polygonfläche, die in jedem Fall gemäß A1(iv) in eine
gewisse Anzahl (etwa l) von kleineren Dreiecksflächen t’ijk zerlegt
werden kann, formal geschrieben:
d’i ∩ ϑ’j
= l⋃kt’ijk.
Sämtliche t’ijk aller dieser Schnittmengen bilden eine neue Zerlegung von p’, die feiner ist als die beiden ursprünglichen Zerlegungen { d’1, ..., d’n } und { ϑ’1, ..., ϑ’m } von p’:
p’ = ⋃kt’ijk.
Sei nun für 1 ≤ i ≤ n φi die (nach A11 eindeutig bestimmte) Isometrie, welche di auf d’i abbildet und
tijk =def φ−1(t’ijk).
Dann gilt für jedes di
di = ⋃j,ktijk.
Entsprechend sei für 1 ≤ j ≤ m ψj diejenige Isometrie, welche ϑ*j auf ϑ’j abbildet und
t*ijk =def ψ−1(t’ijk).
Dann gilt für jedes ϑ*j
ϑ*j = ⋃i,kt*ijk.
Insgesamt führt dies zu
p = ⋃i,j,ktijk und p* = ⋃i,j,kt*ijk
und es gilt tijk ≅ t*ijk wegen tijk ≅ t’ijk und t’ijk ≅ t*ijk für alle diese Teildreiecke. Dies war zu zeigen.
![]() A16
A16
Die Relation „inhaltsgleich“ ist eine Äquivalenzrelation.
Beweis:
Wie eben genügt es, die Transitivität zu zeigen. Hierzu
seien drei Polygonflächen p, p’
und p* gegeben, und zwar derart, dass p
und p’ bzw. p’
und p* inhaltsgleich sind. Gegeben
seien ferner Polygonflächen q,
q’, r’ und
r* mit q z q’
bzw. r’ z r*.
Es sei hierbei vorausgesetzt, dass p
und q, p’
und q’, p’
und r’ bzw. p*
und r* sich nicht überlappen. Nach Definition gilt dann
p ∪ q z p’ ∪ q’
bzw. p’ ∪ r’ z p* ∪ r*.
Es folgt p ∪ q ∪ r’ z p’ ∪ q’ ∪ r’
und p’ ∪ r’ ∪ q’ z p* ∪ r* ∪ q’,
wobei es so eingerichtet werden kann, dass unzulässige Überlappungen nirgends auftreten. Mit A15 folgt
p ∪ q ∪ r’ z p* ∪ r* ∪ q’.
Wegen q ∪ r’ z r* ∪ q’
folgt die Inhaltsgleichheit von p
und p*, was zu zeigen war.
![]() A17
A17
Sei ABC ein beliebiges Dreieck, h die Parallele zu gAB
durch C sowie m die Mittelparallele zu
gAB und h. Seien ferner D, E und F die Fußpunkte der
Lotstrecken von A, C bzw. B auf m. Dann sind das
Dreieck ABC und das Rechteck ABFD zerlegungsgleich.
Beweis:
Sei ein Dreieck ABC beliebig gewählt. Die im Satz
definierten Geraden h und m sind nach X28
und dem Parallelenaxiom,
die Lotfußpunkte D, E und F nach X30 eindeutig bestimmt.


Unter Verwendung von X17, X50 und X35 hat man in jedem Fall SDA ≅ SEC und TCE ≅ TBF und somit ABC z ABFD.
Aus A17 folgt in Verbindung mit A15 sofort
![]() A18
A18
Seien ABC und A’B’C’ zwei Dreiecke, deren Seiten c und c’
die gleiche Länge haben: c = c’. Wenn dann auch die Höhen
hc und hc’ gleichlang sind, so sind ABC und A’B’C’ zerlegungsgleich.
Erfüllen die Dreiecke ABC und A’B’C’ die Voraussetzungen des vorigen Satzes, so gilt wegen A4 auch α(ABC) = α(A’B’C’).
![]() A19
A19
Zu jedem Rechteck ABCD gibt es ein zerlegungsgleiches Rechteck A*B*C*D* mit
|A*B*| = 1.
Beweis:
Gegeben sei ein Rechteck ABCD mit |AB| ǂ 1. Dann erhält man
durch sukzessives Halbieren mit anschließendem Umordnen der Teilrechtecke ein zu ABCD zerlegungsgleiches Rechteck
A’B’C’D’, so dass
|A’B’| ≤ 1 < 2·|A’B’|.

Im Fall |A’B’| = 1 ist nichts mehr zu zeigen. Im Fall |A’B’| ǂ 1 sei E derjenige Punkt auf der durch A’ und B’ gehenden Geraden g, so dass |A’E| = 1. Der Schnittpunkt von D’E und B’C’ sei mit S bezeichnet. T sei der eindeutig bestimmte Punkt zwischen A’ und D’ mit |D’T| = |B’S|. Sei ferner h die Parallele zu g durch T sowie F, G und H die Schnittpunkte von h mit der Strecke D’E, mit B’C’ bzw. mit der Lotgeraden in E zu g.
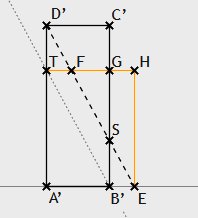
Nach Konstruktion gilt TFD’ ≅ B’ES und somit TF ≡ B’E. Hieraus folgt FH ≡ A’B’ bzw. FH ≡ D’C’, sowie EH ≡ A’T bzw. EH ≡ SC’. Dies bedeutet, dass EHF ≅ SC’D’ und damit ist mit A’EHT das gewünschte Rechteck gefunden.
![]() A20
A20
Zur Fläche eines einfachen Polygons p kann stets ein
Rechteck r konstruiert werden, dessen eine Seite die Länge 1 hat und für das
p z r
gilt.
Beweis:
Aus dem Zwei-Ohren-Theorem folgt, dass man von jedem einfachen Polygon
p mit mehr als drei Eckpunkten solange sukzessiv jeweils ein Dreieck abtrennen kann, bis schließlich nur noch
ein Dreieck übrig bleibt. Zu jedem dieser Dreiecke gibt es nach A17 jeweils
ein zerlegungsgleiches Rechteck. Nach A19 kann man es so bewerkstelligen,
dass jeweils eine Seite aller dieser Rechtecke die Länge 1 haben, so dass man sie zu einem Gesamtrechteck
„übereinander stapeln“ kann, dessen Fläche zerlegungsgleich zu p ist.
![]() A21 (Satz von Bolyai-Gerwien)
A21 (Satz von Bolyai-Gerwien)
Gilt für zwei Polygonflächen p und p* α(p) = α(p*),
so sind p und p*
zerlegungsgleich.
Beweis:
Zu zwei Polygonflächen p und p* mit gleichem
Flächenmaß gibt es nach A20 stets zwei gleichbreite Rechteckflächen r und
r*, so dass
p z r
bzw. p* z r*.
Nach Voraussetzung ist α(p) = α(p*),
also gilt nach A14 ebenso
α(r) = α(r*),
womit r und r* nicht nur gleichbreit, sondern auch gleichhoch sind. Somit sind r und
r* deckungsgleich und demzufolge offensichtlich zerlegungsgleich.
Mit A15 folgt die Behauptung.
![]() A22
A22
Für zwei inhaltsgleiche Polygonflächen p und p* gilt α(p) = α(p*).
Beweis:
Seien die Polygonflächen p und p*
inhaltsgleich. Dann gibt es nach Definition zwei zerlegungsgleiche Polygonflächen
q und q*, welche man überlappungsfrei
p bzw. p* hinzufügen kann, so dass
p ∪ q z p* ∪ q*
gilt. Nach A14 folgt demnach sowohl
α(p ∪ q) = α(p* ∪ q*)
als auch α(q) = α(q*).
Aus diesen beiden Gleichungen folgt mit (F2)
α(p) = α(p*),
was zu beweisen war.
Aus A22 folgt mit A4 sofort
![]() A23
A23
Haben zwei inhaltsgleiche Dreiecke gleichlange Grundseiten g und
g*, so sind die Höhen hg und hg* auch gleichlang.
Sind zwei inhaltsgleiche Rechtecke gleichbreit, so sind sie auch gleichhoch.
![]() A24
A24
Zwei Polygonflächen p und p*
mit gleichem Flächenmaß sind inhaltsgleich.
Beweis:
Seien p und p*
zwei Polygonflächen mit
α(p) = α(p*).
Gemäß A20 gibt es zwei gleichbreite Rechtecke r und r*, so dass
p z r
bzw. p* z r*
gilt. Nach A13(iii) sind deshalb sowohl
p und r
als auch p* und r*
jeweils inhaltsgleich. Mit A22 folgt somit
α(p) = α(r) bzw. α(p*) = α(r*).
Nach Voraussetzung ist α(p) = α(p*), also gilt auch α(r) = α(r*), weswegen die gleichbreiten Rechtecke r und r* auch gleichhoch sind. Demzufolge sind r und r* deckungsgleich und damit zerlegungsgleich. Wegen der Transitivität von z folgt die Zerlegungsgleichheit von p und p* und damit ihre Inhaltsgleichheit.
Es ergibt sich nunmehr zusammenfassend:
![]() A25
A25
Seien p und p*
die Flächen zweier einfacher Polygone. Dann sind die Aussagen
p und p*
sind zerlegungsgleich;
p und p*
sind inhaltsgleich;
α(p) = α(p*)
äquivalent zueinander.
![]() A26 (Satz des Pythagoras)
A26 (Satz des Pythagoras)
Seien p und p*
die Flächen der Quadrate über den Katheten eines rechtwinkligen Dreiecks
ABC und q die Fläche des Quadrates über seiner Hypotenuse.
Dann sind p ∪ p*
und q inhaltsgleich.
Der Beweis gelingt zum Beispiel mittels der folgenden Figur. Die Idee, den Pythagoräischen Satz so zu beweisen, stammt von Martin Wagenschein (M. Wagenschein: Verstehen lehren, S.126).
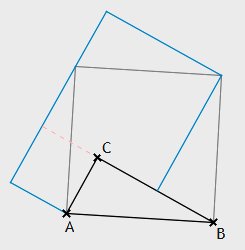
Aus A26 folgt unmittelbar
c2 = a2 + b2.
Hierbei sind a, b und c die Längen derjenigen Seiten, die den Eckpunkten A, B bzw. C eines rechtwinkligen Dreiecks gegenüber liegen.
Diese Gleichung kann auch auf ganz andere Art bewiesen werden; siehe: Satzgruppe des Pythagoras.
Dieses Kapitel wird noch weiter bearbeitet.
Literatur- und Quellenangaben:
Paul Gerwien:
Zerschneidung jeder beliebigen Anzahl von gleichen geradlinigen Figuren in
dieselben Stücke.
Journal für die reine und angewandte Mathematik, Zehnter Band Berlin 1833
Heft III Abhandlung 16, S. 228–234
David Hilbert:
Grundlagen der Geometrie
B. G.Teubner, Leipzig 1903
Gary Hosler Meisters:
Polygons Have Ears
in: The
American Mathematical Monthly, Vol. 82, No. 6, 1975, pp. 648–651
Hrsg.:
Mathematical Association of America
Hans Freudenthal:
Mathematik als pädagogische Aufgabe, Band 1
Klett Verlag, Stuttgart, 2. Auflage 1977
Martin Wagenschein:
Verstehen lehren
Beltz Verlag, Weinheim und Basel, 6. Auflage 1977
Andreas Paffenholz:
Elementargeometrie
Vorlesung an der FU Berlin 2007
Dieter Neßelmann:
Axiomatische Geometrie
Vorlesung an der Universität Rostock 2010
Christian Blatter:
Drei Sätze über ebene Polygonzüge
in: Bulletin N° 119, S. 12−19, 2012
Hrsg.: Verein Schweizerischer Mathematik- und Physiklehrkräfte
Physikalisch-Technische Bundesanstalt:
Die gesetzlichen Einheiten in Deutschland 2. Auflage 2020
Bundesministerium für Wirtschaft und Energie
