Näherungsweise Bestimmung von Pi
Die Fläche eines Zwölftelkreises mit dem Radius 1 wird approximiert mit Hilfe
der Summe der Flächeninhalte geeignet gewählter Rechtecke.
n = Anzahl der Rechteckstreifen:
> restart; with(student): with(plots):
> n:= 5;
Diagramm1:= rightbox(sqrt (1-x^2), x = 0..0.5, n,
scaling = constrained,
colour = red,
thickness = 3,
shading = yellow,
labels = ["", ""]):
Diagramm2:= leftbox(sqrt (1-x^2), x = 0..0.5, n,
scaling = constrained,
colour = red,
thickness = 3,
shading = green,
labels = ["", ""]):
Radien:= plot([[[0, 0], [0.5, sqrt(3)/2]],
[[0, 0], [0, 1]]], x = 0..0.5,
color = red,
thickness = 3):
display([Diagramm1, Radien]);
display([Diagramm2, Radien]);
scaling = constrained,
colour = red,
thickness = 3,
shading = yellow,
labels = ["", ""]):
Diagramm2:= leftbox(sqrt (1-x^2), x = 0..0.5, n,
scaling = constrained,
colour = red,
thickness = 3,
shading = green,
labels = ["", ""]):
Radien:= plot([[[0, 0], [0.5, sqrt(3)/2]],
[[0, 0], [0, 1]]], x = 0..0.5,
color = red,
thickness = 3):
display([Diagramm1, Radien]);
display([Diagramm2, Radien]);
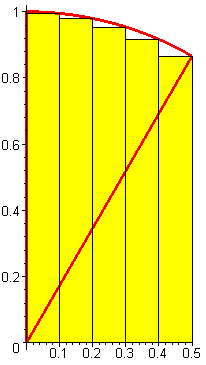
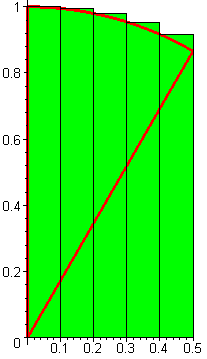
Berechnung der Summe aller gelben bzw. aller grünen Rechteckflächen:
> A[gelb]:= evalf(rightsum(sqrt (1-x^2), x =0..0.5, n));
A[gruen]:= evalf(leftsum(sqrt (1-x^2), x =0..0.5, n));
![A[gelb] := .4711263078](images-pi/pi5.gif){kind=small}
![A[gruen] := .4845237675](images-pi/pi6.gif){kind=small}
π liegt im angegebenen Intervall:
> u:= evalf(12*(A[gelb] - 0.25*sqrt(3)/2)):
o:= evalf(12*(A[gruen] - 0.25*sqrt(3)/2)):
[u, o];
[u, o];
![[3.055439482, 3.216208998]](images-pi/pi8.gif){kind=small}
Näherungswert für π bei 5 Rechteckstreifen:
> pi:= (u + o)/2;
