Integrale und komplexe Zahlen
> restart; with(plots):
Digits:= 20:
interface(displayprecision = 4):
> f:= x -> 1/(1 - x + x^4);

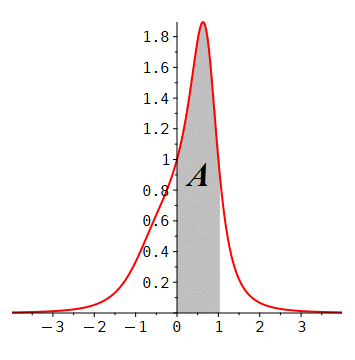
> Graph:= plot(f(x), x = -4..4,
thickness = 2,
color = red,
size = [350, 350].
axesfont = [Courier, 12],
labelfont = [Courier, 13]):
Fläche:= seq(plot([[i/30, 0], [i/30, f(i/30)]],
color = gray,
thickness = 3),
i = 1..30):
TextA:= textplot ([1/2, 0.9, `A`],
font = [TIMES, BOLD, 25]):
display([Fläche, Graph, TextA]);
color = red,
size = [350, 350].
axesfont = [Courier, 12],
labelfont = [Courier, 13]):
Fläche:= seq(plot([[i/30, 0], [i/30, f(i/30)]],
color = gray,
thickness = 3),
i = 1..30):
TextA:= textplot ([1/2, 0.9, `A`],
font = [TIMES, BOLD, 25]):
display([Fläche, Graph, TextA]);
> F(x):= Int(f(x),x);

Lösung dieses unbestimmten Integrals:
> F(x):= simplify(value(F(x)));
![]()
Die "Probe":
> simplify(diff(F(x),x));
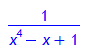
Lösung der Gleichung z4 − z + 1 = 0 im Komplexen:
> lgn:= fsolve(Z^4 - Z + 1, Z, complex):
for i to 4 do l[i]:= lgn[i] od;

Hinschreiben des Funktionsterms F(x) mit Hilfe der Lösungswerte l1, l2, l3 und l4:
> for i to 4 do
lnTerm[i]:= (ln(x - l[i]))/(4*l[i]^3 -
1):
od:
i:= 'i':
F(x):= sum(lnTerm[i], i = 1..4);
od:
i:= 'i':
F(x):= sum(lnTerm[i], i = 1..4);

Berechnung des Flächeninhalts der grauen Fläche A:
> F1:= evalc(eval(FSum, x = 1));
F0:= evalc(eval(FSum, x = 0));
A:= Re(F1 - F0);
A:= Re(F1 - F0);
![]()
![]()
![]()
Den Wert für A erhält man einfacher, aber vordergründiger auch so:
> evalf(Int(f(x), x = 0..1));
![]()
> A[gesamt]:= Int(f(x), x = -infinity..infinity);
A[gesamt]:= evalf(A[gesamt]);
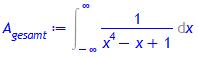
![]()
