Maple-Worksheet: Induktion

Beweis durch vollständige Induktion

> restart;

> Behauptung:= Sum(i^3, i = 1..n) = 1/4*n^2*(n+1)^2;

Induktionsanfang:

> sum(i^3, i = 1..1) - 1/4*1^2*(1+1)^2;

Induktionsannahme: Die Behauptung ist wahr für eine natürliche Zahl n > 0.

> S(n+1):= 1/4*n^2*(n+1)^2 + (n+1)^3;

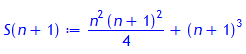
S(n+1) := 1/4*n^2*(n+1)^2+(n+1)^3

Induktionsschluß:

> simplify(S(n+1) - 1/4*(n+1)^2*(n+2)^2);