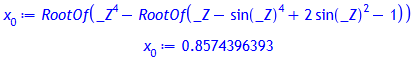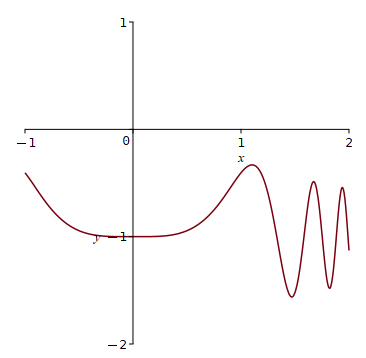dh-Materialien
Maple   Anwendungen

Bestimmen von Nullstellen

> restart;
Digits:= 4:
fnt:= 'font = [COURIER, 12]':

Erstes Beispiel

> f:= x -> x*cos(x):
lgn:= solve (f(x) = 0, x);

lgn:= 0, Pi/2

Mit solve erhält man hier offensichtlich (zunächst) nicht alle Lösungswerte:

> plot(f(x), x = -2*Pi..2*Pi, fnt);

Aber:

> _EnvAllSolutions:= true:
lgn:= solve(f(x) = 0, x);

Eigenschaften der Konstante _Z1:

> about(_Z1);

Originally _Z1, renamed _Z1~:
  is assumed to be: integer

Dies ergibt:

> lgn:= 0, Pi*(k + 1/2);

lgn:= 0, 2*Pi*(k-1/4), 2*Pi*(k+1/4)

Numerische Berechnung einiger Nullstellen von f(x):

> zeros:= {0}:
for i from -5 to 4 do
  zeros:= zeros union {subs(k = i, evalf(lgn[2]))}:
od:
op(sort(convert(zeros, list)));

-14.14, -11.00, -7.855, -4.713, -1.57, 0, ...

Zweites Beispiel

> restart;
Digits:= 4:
fnt:= 'font = [COURIER, 12]':

> f:= x -> 2^x - 0.95*x^2;
  plot(f(x), x = -2..5, y = -4..4, fnt);

f:= x -> 2^x - 0.95*x^2

Mit fsolve erhält man im Allgemeinen jeweils nur einen Lösungswert:

> fsolve(f(x) = 0, x = -2..5);
fsolve(f(x) = 0, x = -1);
fsolve(f(x) = 0, x = 2);
fsolve(f(x) = 0, x = 4);

2.197
-0.7823
2.197
3.705

Aber:

> solve(f(x) = 0, x);

2.197, 3.705, -0.7823

Drittes Beispiel

> restart; 
fnt:= 'font = [COURIER, 12]':

> f:= x -> 0.0008*exp(x)*sin(x) + cos(x)^2;
plot(f(x), x = -15..10, y = -4..4, fnt);

f:= x -> 0.0008*e^x*sin(x) + cos(x)^2

Berechnung einiger Nullstellen von f:

> Digits:= 20:
interface(displayprecision = 10):
zeros:= {}:
for i from -18 to 10 do
  zero:= fsolve(f(x) = 0, x = i):
  if not evalb(zero in zeros) then
    zeros:= zeros union {zero}:
  fi:
od:
liste:= sort(convert(evalf(zeros), list)):
for i from 1 to nops(liste) do
  print(liste[i]);
od;

Nullstellen

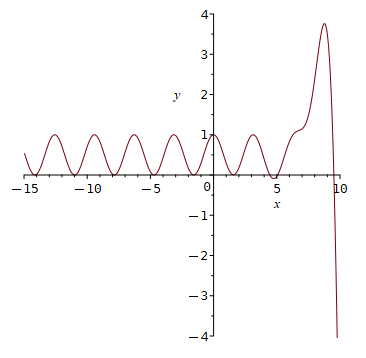
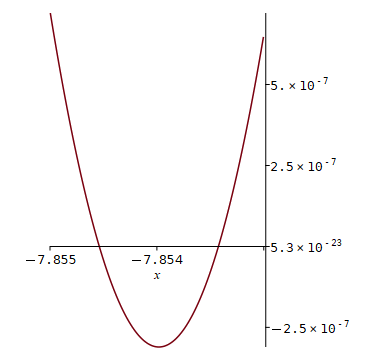
Die Situation in einer kleinen Umgebung von −4,712, bzw. von −7,854:

> plot(f(x), x = -4.714..-4.710, tickmarks = [3,3], fnt);

> plot(f(x), x = -7.855..-7.853, tickmarks = [3,4], fnt);

Viertes Beispiel

> restart;
fnt:= 'font = [COURIER, 12]':
f:= x -> (sin(x^4))/(sqrt(x^2+1))-1;

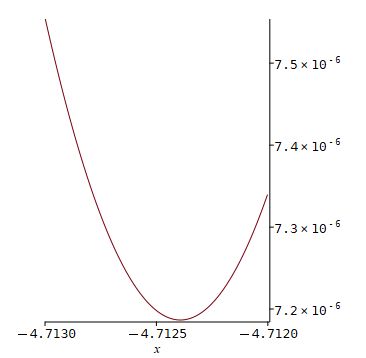
Die Anwendung von solve liefert hier ein falsches Ergebnis:

> x[0]:= solve(f(x) = 0, x);
x[0]:= evalf(%);
f(x[0]);
plot(f(x), x = 0..2, y = -2..1, tickmarks = [4,3], fnt);