dh-Materialien
Maple   Anwendungen

Beschränktes Wachstum

> restart;

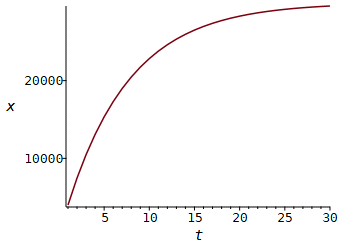
Sei x irgendeine zeitabhängige Größe, von der man weiß, dass die Werte von x nie größer werden können als S. Wenn x sich dann so ändert, dass die Änderungsrate von x proportional ist zu (S − x), dann spricht man von beschränktem Wachstum. Es gilt dann 

∆x  =  x(t+1) − x(t) = k (S − x(t)) 

mit einer Konstanten k. S heißt Wachstumsschranke, (S − x) nennt man Sättigungsmanko.

> Delta[x]:= x -> k*(S - x);

> x[0]:= 0;
S:= 30000;
k:= 40/300;

x[0] := 0
S := 30000
k := 2/15

> for i from 1 to 30 do
  x[i]:= x[i-1] + Delta[x](x[i-1]):
  printf("%10.0f %10.0f \n", i, x[i-1]);
od:
 

 1         0
 2      4000
 3      7467
 4     10471
 5     13075
 6     15332
 7     17287
 8     18982
 9     20451
10     21725
11     22828
12     23784
13     24613
14     25331
15     25954
16     26493
17     26961
18     27366
19     27717
20     28022
21     28285
22     28514
23     28712
24     28884
25     29033
26     29162
27     29273
28     29370
29     29454
30     29527

> plot ([seq([i, x[i]], i = 1..30)],
  ytickmarks = [10000, 20000, 30000], 
  labels  = [t, x], 
  size  = [350, 250],
  labelfont = [COURIER, 12])
  font = [COURIER, 10]);

beschrw10