Kettenbruch
definiert in: Verhältnis/ Kettenbrüche
Sei n ∈ ℕ, x0 ∈ ℤ und xn ∈ ℕ für alle n > 0. Dann nennt man einen Bruch in der Form
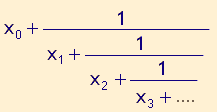
Kettenbruch, abkürzend geschrieben:
<x0; x1; x2; x3; ...>.
Jede irrationale Zahl kann man als unendlichen Kettenbruch darstellen. Umgekehrt gilt: Jeder unendliche Kettenbruch beschreibt eine irrationale Zahl, denn <x0; x1; x2; x3; x4; ...> induziert in natürlicher Weise eine rationale Zahlenfolge
x0, x0 + 1x1, x0 + 1x1 + 1x2 , ... .
und diese unendliche Kettenbruchentwicklung ist eine Cauchyfolge rationaler Zahlen, die in eindeutiger Weise eine reelle Zahl repräsentiert, die nicht rational ist.
Die Kettenbruchentwicklung einer rationalen Zahl bricht nach endlich vielen Iterationsschritten ab. Beispiel:
355113 = <3; 7; 16>.
Die Kettenbruchentwicklung der Kreiszahl π lautet:
π = <3;7;15;1;292;1;1;1;2;1; ...>
Die rekursive Anwendung der Gleichung Φ = 1 + 1Φ liefert die Kettenbruchentwicklung des goldenen Schnittes:
Φ = <1;1;1;1;1;....>
Es ist die einfachste Kettenbruchentwicklung, die man sich vorstellen kann. Sie sorgt dafür, dass Φ diejenige irrationale Zahl ist, die sich am schlechtesten durch eine rationale Zahlenfolge approximieren lässt.
→ Index
