Verhältnis
Relativ wenig − verhältnismäßig viel
![]()
Die gesamte Photovoltaikkapazität Deutschlands betrug im Jahr 2010 etwa 18 GWp. Vergleicht man diesen Wert mit den 114 MWp im Jahr 2000, so sind 18 GWp verhältnismäßig viel (Quelle: BMWi/AGEB). Ende 2020 betrug die in Deutschland installierte Photovoltaikkapazität sogar etwa 53,8 GWp. Dieser Wert ist etwa 470mal größer als derjenige aus dem Jahr 2000! Setzt man die Solarenergie ins Verhältnis zu den konventionellen Energieträgern, dann sieht man, dass der Solaranteil nach wie vor relativ gering ist, obwohl er absolut gesehen (erfreulicherweise) sehr stark angewachsen ist.


2013 betrug der Anteil der Erneuerbaren (Wasserkraft, Windkraft, Biomasse, Photovoltaik, u.a.) an der Gesamtheit aller Energieträger zur Erzeugung elektrischer Energie in Deutschland gemäß der Berechnung nach der Wirkungsgradmethode etwa 25% bzw. nach der Substitutionsmethode etwa 40%. Sieben Jahre später ergaben sich bereits die Werte 44% bzw. über 60%:


Derartige Säulendiagramme und Flächendiagramme kann man nur dann richtig verstehen und interpretieren, wenn man weiß, wie man mit Einheiten rechnet und wie die Prozentrechnung funktioniert.
1 Mrd. kWh ist die Abkürzung für 1 Milliarde Kilowattstunden, das sind 1
Tausend Millionen Kilowattstunden oder anders geschrieben: 1000000000000
Wattstunden, kurz: 1·1012 Wh oder 1 Terawattstunde.
Es gilt 1 Wh = 60 Wmin = 3600 Ws =
3600 J.
Die Vorsilben Kilo, Mega, Giga, Tera und Peta werden benutzt, um sehr große Zahlen zu benennen. Für sehr kleine Zahlen dagegen gibt es die Vorsilben Milli, Mikro, Nano, Pico, Femto und Atto:
| 1 m | = 1000 mm | (1 Meter) | |
| 1 mm | = 1000 µm | = 10-3 m | (1 Millimeter = 1 Tausendstel Meter) |
| 1 µm | = 1000 nm | = 10-6 m | (1 Mikrometer = 1 Millionstel Meter) |
| 1 nm | = 1000 pm | = 10-9 m | (1 Nanometer = 1 Milliardstel Meter) |
| 1 pm | = 1000 fm | = 10-12 m | (1 Picometer = 1 Billionstel Meter) |
| 1 fm | = 1000 am | = 10-15 m | (1 Femtometer = 1 Billiardstel Meter) |
Manchmal ist es zweckmäßig, für uns unvorstellbar riesige oder aber auch unvorstellbar winzige Dinge in einem gewissen Verhältnis zu verkleinern beziehungsweise zu vergrößern, damit wir sie uns in Größenordnungen vorstellen können, die uns aus dem täglichen Leben einigermaßen vertraut sind (1 Zehntel Millimeter bis vielleicht 1000 Kilometer).
Beispielsweise liefert die Verkleinerung eines Teils unseres Sonnensystems im Verhältnis 1500000 : 1 das Folgende:
| Durchmesser der Sonne | 1,4·106 km | 0,933 m |
| Durchmesser der Erde | 1,27·104 km | 0,0085 m |
| Durchmesser des Mondes | 3,5·103 km | 0,0023 m |
| mittl. Entf. Erde − Mond | 3,84·105 km | 0,256 m |
| mittl. Entf. Sonne − Erde | 1,5·108 km | 100,00 m |
Bildet man den Quotienten aus zwei Zahlenwerten oder aus zwei Größen, um vergleichbare Dinge zueinander in Beziehung zu setzen, so nennt man diesen Quotienten Verhältnis.
Setzt man zwei Verhältnisse einander gleich, so erhält man eine Verhältnisgleichung.
Viele physikalische Größen sind definiert als Verhältnis zweier verschiedener Größen, so zum Beispiel die Dichte ρ als Verhältnis der Masse eines homogenen Körpers zu seinem Volumen, oder die Geschwindigkeit v eines sich gleichförmig bewegenden Körpers als Verhältnis zwischen dem zurück gelegten Weg und der dafür benötigten Zeit, oder die Kapazität eines Kondensators als Verhältnis der Kondensatorladung zur angelegten elektrischen Spannung.
Die Grundlage der Prozentrechnung ist die Verhältnisgleichung
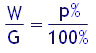
Der Wert W (Prozentwert) irgendeiner Größe wird hierbei ins Verhältnis gesetzt zu einem Bezugswert G (Grundwert). p% heißt Prozentsatz. 1% steht abkürzend für 1100 („ein Hundertstel“), p% ist dasselbe wie p100, 100% sind gleich 100100.
Prozentrechnung ist immer eine Rechnung relativ zu einem Grundwert. Die Angabe eines Prozentwertes W und dem dazugehörigen Prozentsatz p ist demnach nur dann sinnvoll, wenn man weiß, welche inhaltliche Bedeutung der Grundwert G hat.
Das Snellius’sche Brechungsgesetz
![]()
Das nach dem niederländischen Astronomen und Mathematiker Willebrord Snell van Roijen (1591−1626) benannte Brechungsgesetz beschreibt das Verhalten von Licht beim Übergang von einem transparenten Medium in ein anderes. Trifft ein schmales Lichtbündel auf eine plane Grenzschicht zwischen zwei solchen Medien, dann wird ein Teil des Lichts reflektiert und der andere Teil des Lichts gebrochen. Diese Lichtbrechung gehorcht nach Snellius der folgenden Verhältnisgleichung:
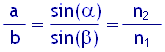
In der folgenden Abbildung ist erklärt, was a, b, α und β bedeuten. Der Winkel α heißt Einfallswinkel, β ist der Brechungswinkel, n2 und n1 sind Materialkonstanten („absolute Brechungsindizes“). Kurz gesagt: Bei der Lichtbrechung ist das Verhältnis sin(α)sin(β) konstant. Der Wert der Konstante n2n1 ist charakteristisch für die verwendeten Materialien und beträgt im hier abgebildeten Beispiel 1,3.
Es gilt a = sin(α) und b = sin(β) genau dann, wenn der Radius des grau eingezeichneten Kreises die Länge 1 hat.
Das Reflexionsgesetz (Einfallswinkel = Ausfallswinkel) und das Brechungsgesetz sind grundlegend für die elementare Strahlenoptik.
Der italienische Universalgelehrte und Renaissance-Baumeister Leone
Battista Alberti (1404−1472) definierte die Schönheit eines Bauwerks als
„Harmonie und Zusammenklang aller Teile, die dort erreicht wird, wo nichts
zugefügt, nichts weggenommen und nichts verändert werden kann, ohne dass das
Ganze beeinträchtigt wird“. Die Struktur der von Alberti entworfenen
Fassade des Palazzo Rucellai in Florenz
zum Beispiel beruht auf ganz bestimmten Zahlenverhältnissen, die auch für
die Harmonielehre der Musik grundlegend sind. Das Geheimnis dieser
Zahlenverhältnisse kann man sich erschließen durch eine Untersuchung der Teilungen von Strecken.
Seien zwei Punkte A und B (in der euklidischen Ebene) gegeben. Dann soll die Strecke mit den Endpunkten A und B „AB“ heißen; „|AB|“ bezeichnet den Abstand zwischen A und B.
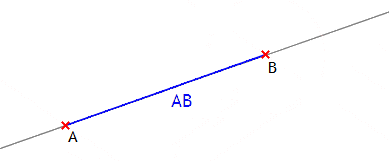
Es
gilt offensichtlich |AB| = |BA|.
Durch zwei Punkte A und B sei eine Gerade gegeben. Sei T ein dritter Punkt auf dieser Geraden. Dann heißt das Streckenverhältnis |TA|:|TB| das Teilverhältnis des Punktes T in Bezug auf die Strecke AB. Liegt T zwischen A und B, so heißt T innerer Teilpunkt. AB wird dann durch T innen geteilt. Liegt T außerhalb von AB, so wird T äußerer Teilpunkt genannt. AB wird dann durch T außen geteilt.
Zu jeder Strecke AB und zu
einem beliebig vorgegebenen Verhältnis r:s gibt es jeweils genau einen
inneren und genau einen äußeren Teilpunkt.
Beweis:
Eine beliebige Strecke AB werde durch einen Punkt T im Verhältnis r:s geteilt.
Fall 1: T ist innerer Teilpunkt.
Wird T innerhalb der Strecke AB in Richtung A verschoben, so wird der Zähler des Bruches rs
verkleinert und der Nenner dieses Bruches gleichzeitig vergrößert;
wird T in Richtung B verschoben, so wird der Zähler des Bruches rs
vergößert und gleichzeitig der Nenner verkleinert. In jedem Fall
ändert sich der Wert des Bruches rs und damit das Teilverhältnis.
Fall 2: T ist äußerer Teilpunkt.
Wird T außerhalb der Strecke AB verschoben, so verändern sich Zähler und Nenner des Bruches rs in
gleicher Weise um einen Wert x.
Es gilt aber einerseits
r+xs+x = (r+x)·s(s+x)·s = rs+xs(s+x)·s
und andererseits
rs = (s+x)·r(s+x)·s = rs+xr(s+x)·s.
Weil T die Strecke AB außen
teilt, ist entweder |TA| < |TB| oder |TA| > |TB|, das heißt, r ǂ s.
Hieraus folgt die Behauptung.
Wird eine Strecke AB durch die Punkte Ti und Ta innen und außen in demselben Verhältnis geteilt, so ist AB harmonisch geteilt. Die vier Punkte A, B, Ti und Ta heißen dann harmonische Punkte.
Gegeben sei eine beliebige Strecke AB und ein innerer Teilpunkt Ti. Ta ist so zu konstruieren, dass AB harmonisch geteilt wird. Die folgende Abbildung zeigt die Lösung dieser Aufgabe. Es ist schnell einzusehen, dass hierbei Ti nicht genau in der Mitte zwischen A und B liegen darf.
Wird eine Saite in einfachen Zahlenverhältnissen abgegriffen und dann angeschlagen, hört man Töne, die harmonisch zueinander passen. Die folgende Darstellung zeigt eine zwischen den Punkten O und A eingespannte Saite. Nimmt man an, dass sich O an der Stelle 0 und A an der Stelle 1 befindet, so befindet sich der eingezeichnete Griffpunkt B an der Stelle 13, das heißt, B teilt die gesamte Saite im Verhältnis 1 zu 2. Seien Ti und Ta zwei weitere Griffpunkte, Ti an der Stelle ti und Ta an der Stelle ta. Dann wird die Strecke AB genau dann von Ti und Ta harmonisch geteilt, wenn die Verhältnisgleichung
1−titi − 1/3 = 1−ta1/3 − ta
erfüllt ist. Das liefert beispielsweise für ta = 14 den Wert ti = 25. Für ta = 0 ergibt sich ti = 12, usw.
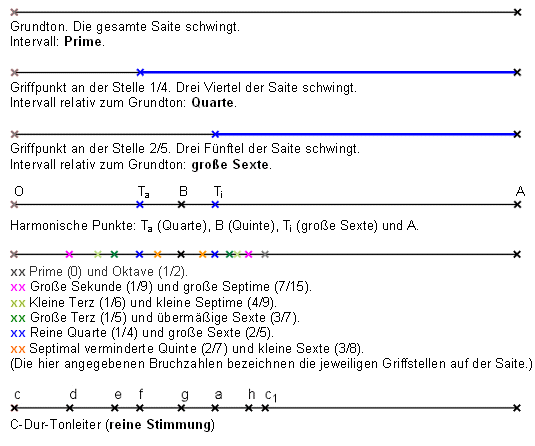
Durch Konstruktion ergibt sich so die Einteilung einer Oktave in zwölf Halbtonschritte, die in der folgenden Tabelle aufgelistet sind. s bezeichnet dabei die Griffstelle des jeweiligen Tons, k gibt den klingenden Teil der Saite an, V ist das Verhältnis der Frequenz des jeweiligen Tones zur Frequenz des Grundtons, v ist dieses Frequenzverhältnis als Dezimalzahl geschrieben.
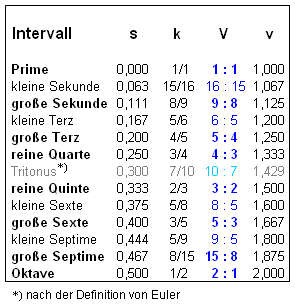
Die Frequenz eines Tones hängt umgekehrt proportional von der Länge der schwingenden Saite ab. Zum Beispiel ergibt eine Halbierung der Saite die Verdoppelung der Frequenz. Durch fortgesetzte Halbierung einer Saite erhält man aneinander gehängte Oktaven:
Die Frequenz des Tones c1 ist doppelt so hoch, die von c2 viermal, die von c3 achtmal so hoch im Vergleich zur Frequenz von c, und so fort. Kurz geschrieben: f(ck) = 2k·f(c). Unser Hörempfinden allerdings läuft dieser Gleichung zuwider, denn wir haben vom Hören her den Eindruck, die Tonhöhe von c2 sei dreimal, die von c3 viermal so hoch usw. relativ zur Tonhöhe von c. Dies liegt daran, dass wir Intervalle mit gleichem Frequenzverhältnis als gleich groß empfinden.
Es gibt für alle anderen Intervalle analoge Gleichungen. Die quintenweise Intervallvergrößerung beispielsweise liefert die Vergrößerung der Frequenz gemäß der Gleichung f(tk) = (32)k·f(t0), wobei t0 irgendein beliebiger Grundton ist. Es gilt f(tk)f(tk−1) = 32 für alle k = 1, 2, 3, .... und dennoch meinen wir zu hören, dass die Differenz von f(tk) und f(tk−1) konstant ist und nicht der Quotient von f(tk) und f(tk−1), wie es tatsächlich der Fall ist.
Um Intervallvergrößerungen gemäß unserem subjektiven Hörempfinden mathematisch beschreiben zu können, müssen wir logarithmieren. Aus der Gleichung f(tk)f(tk−1) = q folgt
lg (f(tk)f(tk−1)) = lg (f(tk)) − lg (f(tk−1)) = lg(q).
Das bedeutet: Vergrößern wir ein Intervall schrittweise immer im selben Verhältnis q, dann hören wir nacheinander Töne, bei denen sich die Logarithmen der jeweiligen Frequenzwerte um den festen Wert lg(q) unterscheiden.
Im folgenden Beispiel mit dem Grundton c ist q = 2 und lg(q) = 0,301.
| Ton | c | c1 | c2 | c3 | c4 |
| V | 1:1 | 2:1 | 4:1 | 8:1 | 16:1 |
| v | 1 | 2 | 4 | 8 | 16 |
| lg(v) | 0,000 | 0,301 | 0,602 | 0,903 | 1,204 |
Frequenzverhältnisse mit den in der Tabelle angegebenen Zahlenwerten für lg(v) zu beschreiben, wäre reichlich unhandlich. Deshalb wurde nach einem Vorschlag von Alexander John Ellis (1814−1890) festgelegt, das zu einer Oktave gehörende Frequenzverhältnis durch den logarithmischen Wert 1200 Cent zu beschreiben. Hiernach ergibt sich:
| Ton | c | c1 | c2 | c3 | c4 |
| i in Cent | 0 | 1200 | 2400 | 3600 | 4800 |
Die Umrechnung eines beliebigen Frequenzverhältnisses v ergibt sich demnach mit folgender Formel:
i = 1200·lg(v)lg(2) Cent.
Umgekehrt gilt:
v = 2(i/1200 Cent).
Beispielsweise gilt für eine Quinte
i = 1200·lg(1,5)lg(2) Cent = 701,955 Cent.
Baut man nun unter Benutzung der oben angegebenen Frequenzverhältnisse mit verschiedenen Grundtönen Tonleitern in Halbtonschritten (so genannte chromatische Tonleitern) auf, dann ergibt sich beispielsweise Folgendes:
| Ton | c | cis | d | dis | e | f | fis | g | gis | a | b | h | c1 |
| i | 0 | 112 | 204 | 316 | 386 | 498 | 617 | 702 | 814 | 884 | 1018 | 1088 | 1200 |
| Ton | g | gis | a | b | h | c1 | cis1 | d1 | dis1 | e1 | f1 | fis1 | g1 |
| i | 702 | 814 | 906 | 1018 | 1088 | 1200 | ... | ||||||
| Ton | d | dis | e | f | fis | g | gis | a | b | h | c1 | cis1 | d1 |
| i | 204 | 316 | 408 | 520 | 590 | 702 | 821 | 906 | 1018 | 1088 | 1222 | ... |
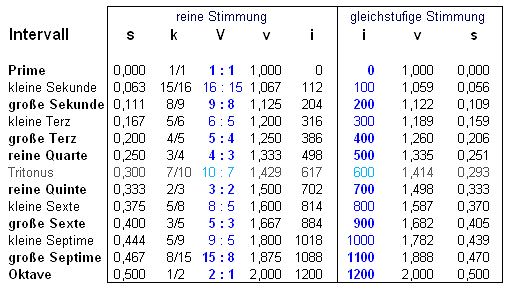
Die so konstruierten Tonleitern sind nicht in sich stimmig. Der Ton a zum Beispiel hört sich auf einer auf c gestimmten Saite völlig anders an als auf einer auf g gestimmten Saite. Lediglich die Töne d, g, b und h klingen in dem hier gewählten Beispiel auf allen Saiten gleich hoch, das heißt mit gleicher Frequenz.
Dieses Dilemma wird mit der gleichstufigen Stimmung beseitigt. Hier gehört zu jedem Halbtonschritt das Frequenzverhältnis v = 2(1/12) ≈ 1,059463 entsprechend 100 Cent („temperierter Halbtonschritt“). An dieser Stelle wird auch spätestens klar, warum Ellis für die Einheit der logarithmisch gemessenen Intervalllänge i den Namen „Cent“ gewählt hat.
1 Cent entspricht dem Frequenzverhältnis 1,005793, das heißt, die beteiligten Frequenzen unterscheiden sich lediglich um knapp 6 Promille.
Proportionen in Architektur und Kunst
![]()
Das erste der folgenden Bilder zeigt ein Teil der von Leone Battista Alberti entworfenen Fassade des Palazzo Rucellai in Florenz, der unter der Leitung von Bernardo Rosselino 1446 gebaut wurde. Das zweite (im Juni 2007 von mir aufgenommene) Bild zeigt eines der unteren Wandstücke im Detail.
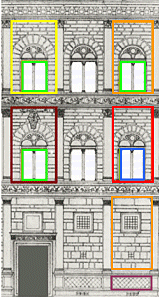

Die regelmäßig wiederkehrenden Pilaster des dreigeschossigen Gebäudes haben keine tragende Funktion, sondern dienen ausschließlich der Gliederung der Fassade. Zwischen den Pilastern des zweiten und dritten Obergeschosses befinden sich nach oben hin durch Rustikabögen abgeschlossene Biforienfenster. Diese Fenster sowie die durch die Pilaster eingerahmten Wandstücke sind nach musikalischen Zahlenverhältnissen proportioniert (vgl. harmonisch geteilte Strecken).
Die Wandstücke über den Portalen (im Bild ist nur eines der zwei Portale wiedergegeben) repräsentieren Sexten (gr. Sexte, 5:3 im 1.OG., dunkelrot; kl. Sexte, 8:5 im 2.OG, gelb), die übrigen, etwas schmaleren Wandstücke repräsentieren Septimen (gr. Sept, 15:8 im 1.OG., rot; kl. Sept, 9:5 im 2.OG. und im EG., orange).
Die Fenster über den Portalen und im 2.OG. entsprechen einer großen Terz (hellgrün), die anderen Fenster einer Quarte (blau).
Alberti hat sich in seinem 1452 veröffentlichten Werk über die Baukunst (De re aedificatoria) stark auf den römischen Baumeister Marcus Vitruvius Pollio (84−27 v.Chr.) bezogen, der im dritten seiner zehn Bücher über Architektur (De architectura libri decem) geschrieben hat:
"Proportion besteht darin, dass in jedem Falle sowohl für die Teile eines Gebäudes als auch für das Ganze eine bestimmte Maßeinheit gilt, wodurch das System der Symmetrie in Kraft tritt. Denn ohne Symmetrie und Proportion kann kein Tempel einen ordentlichen Plan haben; das heißt, er bedarf einer genauen Proportion nach Art der Glieder eines wohlgeformten menschlichen Körpers."
 Vitruvs
Idee, die Maße von Gebäuden nach menschlichen Proportionen auszurichten,
haben viele Baumeister der Renaissance aufgegriffen. Francesco di Giorgio
Martini (1439−1501) hat Ende des 15. Jahrhunderts einen Kirchengrundriss
gezeichnet, nach dem die Gesamtlänge der Kirche in 9¼
Abschnitte geteilt ist, ¼ entsprechend den Füßen eines erwachsenen Mannes,
4 Abschnitte gleich den Beinen, 3½ Abschnitte für den Rumpf und
1½ Abschnitte für den Kopf. Das Mittelschiff seiner Kirche ist genau doppelt
so breit im Vergleich zu den Seitenschiffen, die Länge des Langhauses
entspricht dem Abstand zwischen Bauchnabel und Fußsohle.
Vitruvs
Idee, die Maße von Gebäuden nach menschlichen Proportionen auszurichten,
haben viele Baumeister der Renaissance aufgegriffen. Francesco di Giorgio
Martini (1439−1501) hat Ende des 15. Jahrhunderts einen Kirchengrundriss
gezeichnet, nach dem die Gesamtlänge der Kirche in 9¼
Abschnitte geteilt ist, ¼ entsprechend den Füßen eines erwachsenen Mannes,
4 Abschnitte gleich den Beinen, 3½ Abschnitte für den Rumpf und
1½ Abschnitte für den Kopf. Das Mittelschiff seiner Kirche ist genau doppelt
so breit im Vergleich zu den Seitenschiffen, die Länge des Langhauses
entspricht dem Abstand zwischen Bauchnabel und Fußsohle.
Im Laufe der Zeit wurden die menschlichen Proportionen je nach Zeitgeschmack und mathematischem Ansatz auf ganz verschiedene Weisen versucht zu idealisieren. Der Maler und Grafiker Albrecht Dürer (1471−1528) hat wenig später als Martini den „idealen“ Menschen der Länge nach in 600 Teile geteilt, wovon 29 Teile auf die Füße, 249 auf die Beine, 246 auf den Rumpf und 76 Teile auf den Kopf entfallen.
Das Proportionsschema Dürers ist außerordentlich fein. Beispielsweise steht nach Dürer der Abstand zwischen der Nasenspitze und der Unterkante des Kinns im Verhältnis 1 : 200 zur Gesamtlänge des Menschen.
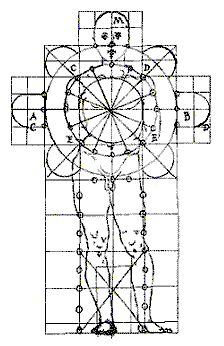
Von Leonardo da Vinci (1452−1519) stammt die berühmte Zeichnung des Mannes mit gespreizten Beinen und schräg ausgestreckten Armen. Dieser Zeichnung liegen die Maßangaben von Vitruv zugrunde.
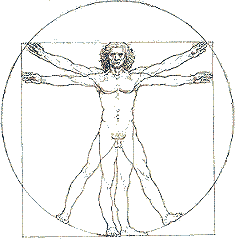
Nach Vitruv bilden 4 Finger eine Handbreite, 4 Handbreiten einen Fuß und 6 Handbreiten eine Elle. Die Höhe eines Mannes misst 24 Handbreiten. Wenn man die Beine so weit spreizt, dass sich die Höhe, gemessen vom Scheitel, um 114 vermindert, und gleichzeitig die Arme so weit öffnet und ausstreckt, dass man mit den Mittelfingern die Waagerechte auf Scheitelhöhe berührt, dann liegen die äußersten Punkte der ausgestreckten Gliedmaßen auf einer Kreislinie. Der Nabel ist der Mittelpunkt dieses Kreises und die Beine bilden zusammen mit der Strecke zwischen den Füßen ein gleichseitiges Dreieck.
Der französisch-schweizerische Architekt, Städteplaner und Maler Le Corbusier (1887−1965) hat im letzten Jahrhundert Wohngebäude konzipiert, die gleichermaßen ästhetisch streng und von der Funktionalität her für die Bewohner ideal sein sollten. Die Proportionen seiner Wohneinheiten beruhten auf dem von ihm entwickelten „Modulor“, dem ein Mensch in durchschnittlicher Größe mit nach oben ausgestrecktem Arm zugrunde liegt. Wesentlich für die Berechnungen von Le Corbusier war das Prinzip des goldenen Schnittes, womit wir beim Thema des nächsten Abschnitts dieses Kapitels wären.
Sei mit AB irgendeine Strecke gegeben und sei T ein innerer Teilpunkt dieser Strecke.
Dann teilt T die Strecke AB genau dann im goldenen Schnitt, wenn das Verhältnis der größeren Teilstrecke zur kleineren Teilstrecke und das Verhältnis der gesamten Strecke zur größeren Teilstrecke gleich groß sind.
Wird die Länge der größeren Teilstrecke mit M („Major“) und die der kleineren Teilstrecke mit m („Minor“) bezeichnet, dann gilt im Fall des goldenen Schnittes die Verhältnisgleichung
Mm = M+mM.
Das Verhältnis Mm wird üblicherweise mit Φ (Phi) bezeichnet und goldene Zahl genannt. Mit dieser Bezeichnung hat man
Φ = 1 + 1Φ.
Hieraus folgt die quadratische Gleichung Φ2 − Φ − 1 = 0 und da Φ nach Voraussetzung eine positive Zahl ist, ergibt sich
Φ = 1+√52.
Demnach ist Φ ≈ 1,618.
Die Konstruktion des goldenen Schnittes verläuft beispielsweise folgendermaßen:
- Zeichne eine Strecke AB.
- Konstruiere das Lot BC in B mit |BC| = 0,5·|AB|.
- Zeichne einen Kreis um C mit dem Radius |CB|.
- Dieser Kreis schneidet die Strecke AC in einem Punkt S.
- Zeichne einen Kreis um A mit dem Radius |AS|.
- Dieser Kreis schneidet die Strecke AB im Punkt T.
Der so konstruierte Punkt T teilt die Strecke AB im goldenen Schnitt.
Beweis:
Sei die Länge von AT mit M und die Länge von TB mit m bezeichnet.
Sei ferner (M+m) = a.
Dann folgt nach der Konstruktion mit dem Satz
des Pythagoras:
(M + a2)2 = a2 + (a2)2.
Also gilt M2 + M·a = a2. Dividieren durch M2
liefert 1 + aM = (aM)2.
Hieraus folgt durch Vergleich mit der Gleichung Φ2 − Φ − 1 = 0 die Behauptung.
Der von Adalbert Göringer erfundene goldene Zirkel ist ein Instrument, bei dem die mittlere Zirkelspitze S die Strecke zwischen den äußeren Zirkelspitzen P und Q immer im goldenen Schnitt teilt. Mit Göringers Zirkel kann man zum Beispiel überprüfen, ob ein Teilpunkt T einer gegebenen Strecke AB diese im goldenen Schnitt teilt oder nicht. In der folgenden Abbildung wird ein solcher Zirkel schematisch dargestellt.
Der goldene Zirkel ist so gebaut, dass U die Strecke PZ im goldenen Schnitt teilt und dass ferner |UP| = |US| und |VS| = |VQ| gilt. Wegen |ZP| = |ZQ| folgt |ZV| = |US| und ZUSV ist ein Parallelogramm. Also hat man ∡UZV = ∡VSU und ∡SUZ = ∡ZVS. Bezeichnet man den ersten Winkel mit α und den zweiten mit β, dann gilt α+β = 180°; mit anderen Worten: α und β sind Nebenwinkel. Also folgt ∡PUS = ∡SVQ = α und damit die Ähnlichkeit der Dreiecke PSU und SQV. Wird ∡SPU mit γ bezeichnet, dann gilt 2·γ + α = 180° und deswegen liegen die Zirkelspitzen P, S und Q auf einer Geraden. Mit dem ersten Strahlensatz folgt, dass wenn U die Strecke PZ im goldenen Schnitt teilt, dasselbe auch für S im Hinblick auf die Strecke PQ gelten muss.
Die Teilung einer gegebenen Strecke im goldenen Schnitt kann auf folgende Art beliebig oft fortgesetzt werden:
T teilt AB im goldenen Schnitt, T1 teilt TA im goldenen Schnitt, und so fort.
Beweis:
Wenn T AB im goldenen Schnitt
teilt, dann folgt mit M = |AT| und m = |TB| aufgrund der Gleichung
Φ = 1 + 1Φ, dass
mM = Mm − 1. Also gilt
mM = M − mm = M − mM − (M − m).
Wegen (M − m) = |AT1| und M − (M − m) = |T1T| teilt T1 die Strecke TA im goldenen Schnitt.
Diesen Konstruktionsschritt kann man beliebig oft wiederholen.
Vielen Baumeistern und Künstlern diente (manchmal nachweislich und zuweilen angeblich) der goldene Schnitt als wichtiges Gestaltungsmittel. Ich gebe an dieser Stelle drei Beispiele: ein berühmtes Beispiel aus der Architektur, ein vielleicht ebenso bekanntes Beispiel aus der Musik und ein wahrscheinlich bisher unbekanntes Beispiel aus der Kunst.
![]() Beispiel 1:
Beispiel 1:
Westseite und Ostseite des zwischen 447 und 432 v.Chr. auf der Spitze der Akropolis in
Athen erbauten Parthenon passten jeweils fast genau in ein goldenes
Rechteck, bei dem die Länge zur Breite im Verhältnis
Φ:1
steht (Abbildung unter Benutzung eines Bildes von Roy George:
The East Side of the Parthenon![]() ).
).

![]() Beispiel 2:
Beispiel 2:
Béla Bartóks Sonate für zwei Klaviere und Schlagzeug besteht aus vier
Sätzen und ist insgesamt 6432 Achtelnoten lang. Der erste Satz Assai lento
- allegro molto endet mit der 3975ten Achtelnote. Die prozentuale
Abweichung von 64323975 relativ zu Φ
beträgt weniger als 0,005%.
Im 274ten Takt wird der Höhepunkt des ersten Satzes erreicht (Paukenwirbel,
volle Akkorde auf beiden Klavieren fortissimo; es beginnt die Reprise). Der
gesamte erste Satz besteht aus 443 Takten. Es gilt 443274
≈ Φ.
Nach Untersuchungen von Ernö Lendvai ist der goldene Schnitt ein ganz
wesentliches Merkmal bei zahlreichen Kompositionen von Bartók.
![]() Beispiel 3:
Beispiel 3:
Das Kegelbild von Kurt
Schwitters ist eine vor allem aus Spielzeugen seines damals dreijährigen
Sohnes hergestellte Assemblage. Die scheinbar wahllos montierten Bauklötze,
Kegel und anderen Gegenstände folgen jedoch bei genauerem Hinsehen genau
festgelegten Konstruktionsprinzipien. Eines dieser Prinzipien ist der
goldene Schnitt (Kurt
Schwitters - Das Werk![]() ).
).
Der goldene Schnitt steht in sehr enger Beziehung mit dem Pentagramm, das man erhält, wenn man jeden Eckpunkt eines regelmäßigen Fünfecks mit dem jeweils übernächsten Eckpunkt geradlinig verbindet. Die so entstehenden Strecken AC, BD, CE, DA und EB sind die Diagonalen des Fünfecks ABCDE.
Je zwei Diagonalen eines regelmäßigen Fünfecks, die keinen Eckpunkt gemeinsam haben, teilen einander im goldenen Schnitt. Beispielsweise teilt T sowohl die Diagonale AD als auch die Diagonale CE im goldenen Schnitt.
Beweis:
ABCDE ist nach Voraussetzung ein regelmäßiges Fünfeck, das heißt, es gilt
|AB| = |BC| = |CD| = |DE| = |EA| und jeder Innenwinkel des Fünfecks ist
gleich weit.
Also sind die Dreiecke ABC, BCD, CDE, DEA und EAB kongruent und
hiermit alle Diagonalen gleich lang.
Aus Symmetriegründen ist AC parallel
zu ED. Ebenso sind AD und BC bzw. EC und AB zueinander parallel. Also ist
ABCT ein Parallelogramm und es gilt |TC| = |AB| und |BC| = |AT|.
Wegen |AB| = |BC| folgt |TC| = |AT|.
Mit |AD| = |EC| und |TC| = |AT| hat man |TD| = |ET|.
Mit dem zweiten Strahlensatz folgt |TD||DE| = |AT||AC| und deswegen gilt auch
|ET||DE| = |TC||AC|.
Wegen |DE| = |AB| = |TC| sowie |AC| = |EC| ergibt sich
|ET||TC| = |TC||EC|.
Hieraus folgt unter Verwendung des ersten Strahlensatz die Behauptung.
Aus dem eben bewiesenen Satz folgt für Pentagramme: Das Verhältnis der Länge einer Diagonalen zur Länge einer Seite ist gleich Φ.
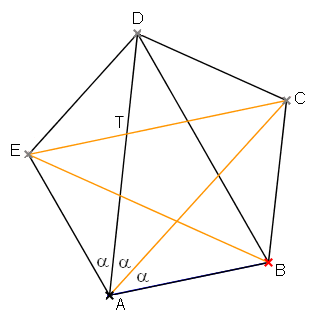
Aufgrund dieser Tatsache ist zum Beispiel das Dreieck ABD ein goldenes Dreieck, denn es ist gleichschenklig und das Verhältnis der Länge eines Schenkels zur Grundseite ist gleich Φ.
ABCT ist eine Raute. Das bedeutet, dass AC den Winkel ∡BAD halbiert. Da jeder Innenwinkel eines regelmäßigen Fünfecks (3·180°)5 = 108° beträgt, gilt für die in der Abbildung gezeigten Winkel α = 36°.
Die Konstruktion eines Pentagramms ist relativ einfach. Eine Möglichkeit besteht darin, mit der Konstruktion eines goldenen Dreiecks ABD zu beginnen.
Das Pentagramm ist eines der ältesten und am weitesten verbreiteten Symbole: Zeichen der Göttin Ischtar im alten Babylon vor viertausend Jahren, antikes Symbol für Harmonie und Gesundheit, Erkennungszeichen der Pythagoräer, bei den Kelten das Zeichen der Erdgöttin Morgan, im Mittelalter Drudenfuß als Schutz gegen Dämonen und böse Geister, esoterisches Symbol mit magischen Kräften, altes kirchliches Symbol zum Beispiel zur Darstellung der fünf Wunden Christi, architektonisches Merkmal gotischer Kirchen, als roter ausgefüllter Fünfstern Symbol des Kommunismus, Bestandteil vieler Staatssymbole. Beispielsweise besteht die europäische Flagge aus zwölf im Kreis regelmäßig angeordneten, goldenen Fünfsternen auf blauem Grund.
Die nach dem französischen Mathematiker Edouard Lucas (1842−1891) benannten Zahlenfolgen beginnen jeweils mit zwei vorgegebenen natürlichen Zahlen. Ab dem dritten Folgenglied gilt die Regel, dass jedes Folgenglied berechnet werden kann durch die Summe seiner beiden Vorgänger. Mit anderen Worten:
Eine Zahlenfolge (xn) heißt genau dann Lucas-Folge, wenn für alle n ∈∈ ℕ mit n > 1 Folgendes gilt:
xn = xn−1 + xn−2 .
Die Lucas-Folge mit x0 = 1 und x1 = 1 heißt Fibonacci-Folge.
Die ersten Folgenglieder der Fibonaccifolge lauten also 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
Mit Hilfe der Fibonaccifolge lässt sich in natürlicher Weise folgende Spirale konstruieren, die nach einem der größten europäischen Mathematiker des Mittelalters Leonardo Pisano (1170−1250) benannt ist (Leonardo nannte sich selbst „Fibonacci“):
Sei (xn) eine Lucas-Folge mit x0 > 0 und x1 > 0. Dann ist die Folge (qn) der Quotienten aufeinander folgender Lucas-Zahlen mit
qn =def xn+1xn für alle n ∈∈ ℕ
konvergent und es gilt
qn → Φ (n → ∞).
Beweis:
Für alle n ∈∈ ℕ mit n > 1 gilt
qn = xn+1xn = xn + xn−1xn = 1 + 1qn−1.
Daraus folgt
Φ − qn = 1 + 1Φ − (1 + 1qn−1) = qn−1 − ΦΦ·qn−1.
Sowohl Φ als auch qn−1 sind positiv, also gilt
|Φ − qn| = |Φ − qn−1|Φ·qn−1.
(xn) ist nach Definition streng monoton wachsend, das heißt: qn−1 > 1 und damit hat man
|Φ − qn| < |Φ − qn−1|Φ.
Hieraus folgt für alle n > 1, dass
|Φ − qn| < |Φ − qn−1|Φ < |Φ − qn−2|Φ2 < ... < |Φ − q2|Φn−2.
Wegen Φ > 1 wird Φn−2 mit wachsendem n beliebig groß, also ist (qn) eine konvergente Zahlenfolge und es gilt qn → Φ (n → ∞).
Der Grenzwert der Folge (qn) ergibt sich auch auf andere Art, wenn man beachtet, dass für alle n ∈∈ ℕ Folgendes gilt:
|xn+12 − xn·xn+1 − xn2| = k.
k ist eine Konstante, die durch die ersten zwei Folgenglieder der Lucas-Folge (xn) festgelegt ist:
k = x12 − x0·x1 − x02
Beweis:
Die behauptete Aussage wird durch
vollständige Induktion
über n bewiesen.
Induktionsanfang:
Die behauptete Aussage gilt natürlich für n = 0.
Induktionsvoraussetzung:
Es gelte |xm+12 − xm·xm+1 − xm2| = k für ein m ∈∈ ℕ.
Induktionsschluss:
|xm+22 − xm+1·xm+2 − xm+12|
= |(xm+1+xm)2−xm+1·(xm+1+xm)−xm+12|
= |2·xm·xm+1 + xm2 − xm+1·xm −
xm+12|
= |−xm+12 + xm·xm+1 + xm2|
= |xm+12 − xm·xm+1 − xm2|
Die Behauptung folgt mit der Induktionsvoraussetzung.
Die Lösung der quadratischen Gleichung xn+12 − xn·xn+1 − xn2 = K mit xn+1 als Variable liefert unter Beachtung, dass xn+1 positiv ist:
xn+1 = xn2 + 12·sqrt(5xn2 + 4K).
K ist hierbei gleich k oder gleich −k.
Division durch xn ergibt mit qn = xn+1xn
qn = 12 + 12·sqrt(5 + 4Kxn2).
Wegen 4Kxn2 → 0 (n → ∞) folgt, dass
qn → 1+√52 (n → ∞) .
Jede relle Zahl x lässt sich in folgender Weise additiv zerlegen:
x = x0 + R0.
Hierbei ist x0 die größte ganze Zahl, die kleiner ist
als x.
Wenn x ∉∉ ℤ, dann ist R0
positiv und kleiner als 1. Die Zahlen x0
und R0 sind eindeutig bestimmt.
Der Kehrwert von R0,
also 1R0, ist wegen R0 < 1 größer als 1.
Er lässt sich auf die gleiche Art zerlegen wie x.
Mit r0 = 1R0
folgt:
x = x0 + 1r0 = x0 + 1x1 + R1.
Wendet man dieselbe Überlegung auf R1 an, so ergibt sich
x = x0 + 1x1 + R1 = x0 + 1x1 + 1x2 + R2 .
Schrittweise fortgesetzt erhält man eine durch x eindeutig bestimmte Zahlenfolge (xn).
Sei n ∈∈ ℕ, x0 ∈∈ ℤ und xn ∈∈ ℕ für alle n > 0. Dann nennt man einen Bruch in der Form
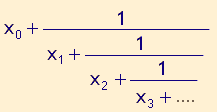
Kettenbruch, abkürzend geschrieben:
<x0; x1; x2; x3; ...>.
Jede irrationale Zahl kann man als unendlichen Kettenbruch darstellen. In diesem Fall sind alle Rn mit n ∈ ℕ größer als 0. Umgekehrt gilt: Jeder unendliche Kettenbruch beschreibt eine irrationale Zahl, denn <x0; x1; x2; x3; x4; ...> induziert in natürlicher Weise eine rationale Zahlenfolge
x0, x0 + 1x1, x0 + 1x1 + 1x2 , ... .
Diese unendliche Kettenbruchfolge ist eine Cauchyfolge rationaler Zahlen und repräsentiert in eindeutiger Weise eine reelle Zahl, die nicht rational ist (vgl. die Untersuchung von Cauchyfolgen im Kapitel Zahlen).
Ist x dagegen eine rationale Zahl, dann gibt es ein Ri mit Ri = 0 und der Kettenbruch endet im i-ten Iterationsschritt.
Die Kettenbruchentwicklung der rationalen Zahl 355113
zum Beispiel ergibt
355113 = <3; 7; 16>.
| 355/113 | ||||
| = | 3 + 16/113 | R0 = | 16/113 | |
| = | 3 + 1/(113/16) | |||
| = | 3 + 1/(7 + 1/16) | R1 = | 1/16 | |
| = | 3 + 1/(7 + 1/(16/1)) | |||
| = | 3 + 1/(7 + 1/(16 + 0)) | R2 = | 0 |
355113 ist das dritte Folgenglied der die Kreiszahl π approximierenden Kettenbruchfolge. Dieser Bruch kommt dem Wert von π schon sehr nahe (der Fehler beträgt lediglich etwa 0,0000085%). Man sieht sehr rasch, warum dies so ist, wenn man sich die Kettenbruchentwicklung von π anschaut.
Mit dem folgenden in JavaScript realisierten Programm lassen sich die Kettenbruchentwicklungen von positiven Zahlen berechnen (→ Quelltext). Hierbei kann x als Bruch (Beispiel: 355/113) oder als Dezimalbruch (Beispiel: 3.14) eingegeben werden. Es sind für x auch folgende Werte zulässig: Pi, Phi, e, ln(2), ln(10), sqrt(2). Phi ist hierbei die goldene Zahl und e die Euler’sche Zahl. Die Iterationstiefe N ist maximal gleich 20.
| n | Kettenbruch | Bruch | Dezimalbruch |
Die rekursive Anwendung der Gleichung Φ = 1 + 1Φ liefert die Kettenbruchentwicklung des goldenen Schnittes:
Φ = <1;1;1;1;1;....>
Es ist die einfachste Kettenbruchentwicklung, die man sich vorstellen kann. Sie sorgt dafür, dass Φ diejenige irrationale Zahl ist, die sich am schlechtesten durch eine rationale Zahlenfolge approximieren lässt.
