Ebene
Die Elemente von Euklid bieten eine systematische und umfassende Darstellung der Mathematik im Griechenland des dritten Jahrhunderts v. Chr. und waren mehr als 2000 Jahre lang zumindest im europäischen Raum die Grundlage für den Mathematikunterricht. Auf der Basis von Definitionen, Postulaten und Axiomen werden die in einzelnen Paragraphen präsentierten Lehrsätze deduktiv abgeleitet. Das I. Buch der Elemente, in dem es um geometrische Grundtatsachen geht, beginnt mit den drei folgenden Definitionen:
1. Ein Punkt ist, was keine Teile hat.
2. Eine Linie breitenlose
Länge.
3. Die Enden einer Linie sind Punkte.
Bereits diese ersten Sätze sind Beispiele dafür, dass Euklid in seinen Definitionen Begriffe vielfach in beschreibender Form erklärt, und zwar ohne dass mit den hierfür verwendeten Wörtern (wie etwa „Teile“, „Länge“ oder „Linie“) eine klare mathematische Bedeutung verbunden wäre. Zudem werden in den Beweisen mancher Lehrsätze Dinge stillschweigend vorausgesetzt, die der bloßen Anschauung geschuldet sind (beispielsweise die Aussage des Axioms von Pasch oder die des sogenannten Crossbar-Theorems).
Gegen Ende des 19. Jahrhunderts haben sich viele Mathematiker − etwa Guiseppe Veronese (1854−1917) oder Moritz Pasch (1843−1930) − darum bemüht, Wege zu finden, um Euklid’s Geometrie logisch einwandfrei neu entwickeln zu können. David Hilbert (1862−1943) hat dann 1899 die Grundsätze der Geometrie in Gestalt von Axiomen formuliert, mit denen keineswegs die grundlegenden geometrischen Objekte wie Punkte, Geraden, Strecken und Ebenen explizit definiert, sondern vielmehr deren gegenseitige Beziehungen festgelegt werden. Diese Beziehungen werden von Hilbert mit Hilfe von Worten wie „bestimmen“, „liegen“, „zwischen“, „kongruent“, ... ausgedrückt.
Indem einige der Hilbert’schen Axiome (nämlich diejenigen, die die räumliche Geometrie betreffen) weggelassen bzw. ein wenig umformuliert werden, erhält man ein Axiomensystem der ebenen euklidischen Geometrie. Das so reduzierte Axiomensystem enthält insgesamt sechzehn Axiome: die ebenen Inzidenzaxiome (I.1 bis I.3), die linearen Anordungsaxiome (II.1 bis II.3), das Axiom von Pasch (II.4), die linearen Kongruenzaxiome (III.1 bis III.3), die ebenen Kongruenzaxiome (III.4 bis III.6), das Parallelenaxiom (IV) und die Axiome der Stetigkeit (V.1 und V.2).
Euklid forderte mit den ersten beiden seiner fünf Postulate im I. Buch der Elemente, dass „man von jedem Punkt nach jedem Punkt die Strecke ziehen“ und dass „man eine begrenzte gerade Linie zusammenhängend gerade verlängern kann“. Auf Euklids Ebene, die man sich als ein flaches, unbegrenztes und nicht gekrümmtes Gebilde vorstellen kann, lassen sich aufgrund gewisser Regeln geometrische Objekte zeichnen und konstruieren.
Dagegen haben die für die Geometrie grundlegenden Axiome von Hilbert, die in diesem Kapitel der Reihe nach vorgestellt werden, nicht von vornherein einen anschaulichen Bezug. Jede der in den folgenden Abschnitten formulierten Aussagen darf nicht ad hoc (weil man es „so sieht“) akzeptiert, sondern muss auf axiomatischer Basis bewiesen werden. Gleichwohl kann Euklids Zeichenebene als anschauliches Modell des (reduzierten) Hilbert’schen Axiomensystems dienen.
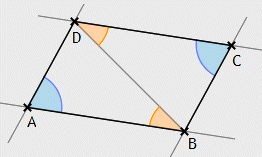
Ebene Inzidenzaxiome
![]() I.1. Zwei voneinander verschiedene Punkte bestimmen stets
genau eine Gerade.
I.1. Zwei voneinander verschiedene Punkte bestimmen stets
genau eine Gerade.
![]() I.2. Irgend zwei voneinander verschiedene Punkte einer Geraden bestimmen diese Gerade.
I.2. Irgend zwei voneinander verschiedene Punkte einer Geraden bestimmen diese Gerade.
![]() I.3. Auf jeder Geraden gibt es wenigstens zwei Punkte. Es gibt wenigstens
drei nicht auf einer Geraden gelegene Punkte.
I.3. Auf jeder Geraden gibt es wenigstens zwei Punkte. Es gibt wenigstens
drei nicht auf einer Geraden gelegene Punkte.
Die durch zwei verschiedene Punkte P und Q nach I.1 eindeutig festgelegte Gerade soll mit gPQ bezeichnet werden. Anschaulich kann man sich unter gPQ ein in zwei Richtungen unbegrenzt weit reichendes geometrisches Objekt vorstellen:

Sind A und B Punkte, die zu gPQ gehören, so sind nach I.2 die Geraden gAB und gPQ identisch; kurz: gAB = gPQ.
Die Sprechweisen „P gehört zu g, „P liegt auf g“, „g geht durch P“ und dergleichen sollen stets denselben Sachverhalt beschreiben.
![]() X1
X1
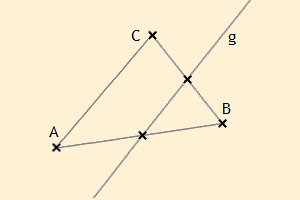
Zwei voneinander verschiedene Geraden haben entweder genau einen oder keinen gemeinsamen Punkt.
Beweis:
Angenommen, g und h seien zwei voneinander verschiedene Geraden mit
mindestens zwei gemeinsamen Punkten. Da nach Axiom I.1 aber jede Gerade bereits durch zwei Punkte eindeutig
bestimmt ist, müssen g und h identisch sein, ein Widerspruch zur Annahme!
Haben zwei Geraden g und h genau einen Punkt S gemeinsam, so sagt man: „g und h schneiden sich in S“ oder „S ist der Schnittpunkt von g und h“. Schneiden g und h sich nicht, so nennt man g und h parallel, in Zeichen: g||h.
Wenn es für drei Punkte heißt, dass einer dieser Punkte zwischen den beiden anderen liegt, so soll vorausgesetzt sein, dass alle drei Punkte auf ein und derselben Geraden liegen.
Lineare Anordnungsaxiome
![]() II.1.
Liegt der Punkt B zwischen den Punkten A und C, so liegt B auch zwischen C und A.
II.1.
Liegt der Punkt B zwischen den Punkten A und C, so liegt B auch zwischen C und A.
![]() II.2. Zu je zwei Punkten A und C gibt es stets wenigstens einen Punkt B, der zwischen A
und C liegt und wenigstens einen Punkt D, so dass C zwischen A und D liegt.
II.2. Zu je zwei Punkten A und C gibt es stets wenigstens einen Punkt B, der zwischen A
und C liegt und wenigstens einen Punkt D, so dass C zwischen A und D liegt.
![]() II.3. Unter irgend drei Punkten einer Geraden gibt es stets genau
einen Punkt, der zwischen den beiden anderen liegt.
II.3. Unter irgend drei Punkten einer Geraden gibt es stets genau
einen Punkt, der zwischen den beiden anderen liegt.
Wenn ein Punkt B zwischen A und C liegt, soll dies kurz mit der Formel _ABC_ ausgedrückt werden. Nach II.1 sind die Ausdrücke _ABC_ und _CBA_ äquivalent.
Drei voneinander verschiedene Punkte heißen genau dann kollinear, wenn diese auf ein und derselben Geraden liegen.
Sind A, B und C kollineare Punkte, so gibt es die drei Möglichkeiten _ABC_, _BCA_ und _CAB_, die sich nach II.3 gegenseitig ausschließen. Nach II.2 gibt es zu zwei Punkten A und C immer zwei weitere Punkte B und D mit _ABC_ bzw. _ACD_.
Mit zwei voneinander verschiedenen Punkten P und Q auf einer Geraden ist eine − mit PQ oder mit QP bezeichnete − Strecke gegeben. Zu dieser Strecke gehören alle Punkte auf gPQ, die zwischen P und Q liegen. P und Q heißen Endpunkte der Strecke PQ.
Aus dem Axiom II.2 folgt insbesondere, dass zu einer Strecke wenigstens ein Punkt gehört.
Ebenes Anordnungsaxiom
![]() II.4. (Axiom von Pasch) Es seien A, B und C drei nicht in gerader Linie gelegene Punkte
und g eine Gerade, die durch keinen dieser Punkte geht. Wenn dann g
durch einen Punkt der Strecke AB geht, so geht sie gewiss
auch entweder durch einen Punkt der Strecke BC
oder durch einen Punkt der Strecke AC.
II.4. (Axiom von Pasch) Es seien A, B und C drei nicht in gerader Linie gelegene Punkte
und g eine Gerade, die durch keinen dieser Punkte geht. Wenn dann g
durch einen Punkt der Strecke AB geht, so geht sie gewiss
auch entweder durch einen Punkt der Strecke BC
oder durch einen Punkt der Strecke AC.
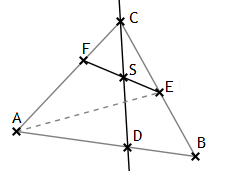
Aus dem Axiom von Pasch folgen unmittelbar die folgenden zwei Aussagen:
![]() X2
X2
Es seien A, B und C drei nicht in gerader Linie gelegene
und voneinander verschiedene Punkte. Die Gerade gA sei
bestimmt durch A und einen beliebigen Punkt der Strecke BC,
die Gerade gB durch B und einen beliebigen
Punkt der Strecke AC und die Gerade gC durch
C und einen beliebigen Punkt der Strecke AB.
(i) Je zwei der drei Geraden gA, gB und gC schneiden sich, und zwar in einem Punkt, der sowohl zwischen den die eine Gerade bestimmenden Punkten als auch den die andere Gerade bestimmenden Punkten liegt.
(ii) Sei E ein beliebiger Punkt zwischen B und C sowie F ein beliebiger Punkt zwischen A und C. Der Schnittpunkt von gC mit AB soll D heißen. Dann schneiden sich gC und EF in einem Punkt S, der sich zwischen D und C, bzw. zwischen E und F befindet.
Bei entsprechender Wahl der Punkte ergeben sich offensichtlich gleichlautende Aussagen für gA bzw. gB.
Beweis:
zu (i): Es reicht aus, einen Fall, beispielsweise den mit gC und gA,
zu diskutieren. Der Schnittpunkt von gC mit AB
soll D, derjenige von gA mit BC
soll E heißen. Die Gerade gC schneidet nicht
EB, denn der (nach
X1 einzige) gemeinsame Punkt C von gC und gBC liegt
nicht zwischen E und B. Unter Verwendung der Punkte A, B und E
folgt mit II.4, dass gC
die Strecke AE und somit gA schneidet.
zu (ii): Betrachtet man gC zunächst (wie unter (i))
relativ zu A, B und E und danach relativ zu A, E und F, so folgt mit
II.4 sofort die Behauptung.
![]() X3
(Satz von Moore)
X3
(Satz von Moore)
Vier beliebige kollineare Punkte lassen
sich stets derart mit A, B, C, D bezeichnen, so
dass der mit B bezeichnete Punkt zwischen A und C und auch zwischen A und D sowie der
mit C bezeichnete Punkt zwischen A und D und auch zwischen B und D liegt.
Dies bedeutet, dass vier auf einer Geraden liegende Punkte angeordnet sind; es gibt unter vier voneinander verschiedenen Punkten immer eine Reihenfolge: einen ersten, dann einen zweiten, dritten und schließlich einen letzten Punkt.

Die Aussage dieses Satzes mag man − anschaulich betrachtet − selbstverständlich finden (und wurde von Hilbert in der ersten Version seines Axiomensystems wenig verwunderlich als Axiom formuliert). Der amerikanische Mathematiker Eliakim Hastings Moore (1862−1932) hat allerdings gezeigt, dass man diese Aussage auf Grundlage der Axiome I.3 und II.1 bis II.4 beweisen kann (E. H. Moore: ON THE PROJEKTIVE AXIOMS OF GEOMETRY, §2):
Beweis:
Vier voneinander verschiedene und auf einer Geraden liegende Punkte seien beliebig gewählt. Für einen dieser
Punkte, etwa mit A bezeichnet, gibt es zwei Möglichkeiten: Entweder liegt A zwischen
zwei der anderen Punkte oder nicht. Im ersten Fall seien die Punkte, zwischen denen A liegt, mit B bzw. C bezeichnet.
Dann gibt es unter der Voraussetzung _CAB_ nach II.3 drei Möglichkeiten
für den vierten Punkt D: _ABD_, _ADB_ sowie _DAB_. Im zweiten Fall muss es neben A noch einen weiteren Punkt geben, etwa B,
der wie A ebenfalls kein „Zwischenpunkt“ ist. Dann gilt _ACB_ und _ADB_.
Wenn man annimmt, dass die vier auf einer Geraden liegenden Punkte A, B, C und D immer angeordnet
sind, dann sind gemäß der eben gemachten Vorbemerkungen alle
möglichen Anordnungen unter Benutzung der Zeichen ˄ (und),
⊻ (entweder oder), ⇀ (wenn, so) durch
die folgenden Aussagen vollständig beschrieben:
(1a) _CAB_ ˄ _ABD_ ⇀ _CAD_;
(1b) _CAB_ ˄ _ABD_ ⇀ _CBD_;
(2a) _CAB_ ˄ _ADB_ ⇀ _CAD_;
(2b) _CAB_ ˄ _ADB_ ⇀ _CDB_;
(3a) _CAB_ ˄ _DAB_ ⇀ _CDA_ ⊻ _DCA_;
_CDA_ ⇀ _CDB_;
(3b) _CAB_ ˄ _DAB_ ⇀ _CDB_ ⊻ _DCB_;
_CDB_ ⇀ _CDA_;
(4a) _ACB_ ˄ _ADB_ ⇀ _ACD_ ⊻ _ADC_;
_ACD_ ⇀ _CDB_;
(4b) _ACB_ ˄ _ADB_ ⇀ _CDB_ ⊻ _DCB_;
_CDB_ ⇀ _ACD_.
Diese Aussagen sind in ihrer Gesamtheit also äquivalent zur Aussage des zu beweisenden Satzes.
Der Beweis des Satzes hat zwei Teile: Erstens wird für vier kollineare Punkte A, B, C und D unter Benutzung der bisherigen Axiome die Aussage
(●) _ABC_ ˄ _ACD_ ⇀ _BCD_
bewiesen; zweitens wird gezeigt, dass aus (●) alle Aussagen (1a) bis (4b) folgen.
Teil I.
Sei für vier beliebig gewählte kollineare Punkte A, B, C und D vorausgesetzt, dass B zwischen A und C sowie C zwischen A und D liegt. Man kann zeigen, dass dann folgende Aussagen wahr sind:
(a) D liegt nicht zwischen B und C.
(b)
B liegt zwischen A und D.
(c) B liegt nicht zwischen C und D.
Aus (a) und (b) folgt wegen II.3, dass C zwischen B und D liegt.
zu (a):
Sei E ein Punkt, der nicht auf der Geraden gAB liegt.
(Die Existenz eines solchen Punktes ist wegen I.3 gesichert.)
Nach II.2 gibt es dann einen Punkt F zwischen E und C. A liegt nicht
zwischen B und C, also geht die Gerade gAF gemäß
II.4 durch einen Punkt, etwa G, der zwischen E und B und zudem zwischen A und F liegt.
Angenommen, D liegt zwischen B und C. Dann folgt unter Anwendung von X2(ii) im Hinblick auf die Punkte E, B und C, dass die Strecke DF von der Geraden gCG geschnitten wird. gCG schneidet zudem AD, denn nach Voraussetzung liegt C zwischen A und D. Da G zwischen A und F liegt, schneidet gCG schließlich auch AF.
Dies liefert einen Widerspruch, denn nach dem Axiom von Pasch kann es keine Gerade geben, welche die drei Strecken DF, FA und AD schneidet. Die Annahme war also falsch. Demnach liegt D nicht zwischen B und C.
zu (b):
Wegen (a) ist _ABC_ ˄ _ACD_ ˄ _CDB_,
also auch _DCA_ ˄ _DAB_ ˄ _ABC_ nicht möglich. Unter der Voraussetzung _ABC_ ˄ _ACD_
liegt also A sicher nicht zwischen D und B.
Die Annahme, dass D zwischen A und B liegt, führt zu _ABC_ ˄ _ACD_ ˄ _ADB_. Allerdings hat man dann wegen (a)
_ABC_ ˄ _ACD_ ⇀
nicht _BDC_
_ACD_ ˄ _ADB_ ⇀
nicht _CBD_
_ADB_ ˄ _ABC_ ⇀
nicht _DCB_
und damit einen Widerspruch zu II.3. Also liegt B zwischen A und D.
zu (c):
Sei E ein Punkt, der nicht auf der Geraden gAC liegt
und F ein Punkt auf EC. A liegt nicht
zwischen C und D, also geht die Gerade gAF gemäß
II.4 durch einen Punkt G, der zwischen E und D liegt. G
liegt nicht zwischen A und F. Ferner liegt B nach Voraussetzung zwischen A
und C, also schneidet die Gerade gBG die Strecke CF
in einem Punkt H.
Aus _CHF_˄ _CFE_ folgt nach (b) _CHE_, womit gBG auch die Strecke CE schneidet. Läge nun B zwischen C und D, so würde gBG nicht nur CE und ED, sondern auch CD schneiden, was aber unmöglich ist. B liegt also nicht zwischen C und D.
Teil II.
(i) zu zeigen: Aus (●) folgt (2a).
(●)
erhält durch Umbenennung der Punkte (A→B,
B→D, C→A,
D→C) die folgende Gestalt:
_BDA_ ˄ _BAC_ ⇀ _DAC_.
Unter Beachtung von II.1 folgt (2a).
(ii) zu zeigen: Aus (2a) folgt (2b).
Sei _CAB_ und _ADB_
vorausgesetzt.
Wäre _DCB_, so würde aus _BAC_ ˄ _BCD_ wegen
(2a) _ACD_ und aus _BCD_ ˄ _BDA_ ebenso wegen (2a) _CDA_ folgen.
_ACD_ und _CDA_ widersprechen sich aber wegen II.3. Wäre
andererseits _CBD_, so würde aus _DBC_ ˄ _BAC_ wegen (2a)
_DBA_ folgen, im Widerspruch zu _ADB_. Da nunmehr sowohl _CDA_ als auch
_DBA_ ausgeschlossen sind, bleibt als dritte Möglichkeit nur _CDB_ übrig. Es gilt also
_CAB_ ˄ _ADB_ ⇀ _CDB_,
wie zu zeigen war.
(iii) zu zeigen: (1a) sowie (1b) folgen aus (2a) und (2b).
(1a) und
(1b) sind äquivalent, denn sie entsprechen beide der Anordnung „CABD“ bzw. „DBAC“. Es genügt also, die Gültigkeit von
(1a) nachzuweisen.
Sei _CAB_ und _ABD_ vorausgesetzt.
Wäre _CDA_, so würde aus _BAC_ ˄ _ADC_ wegen (2a) _BAD_
folgen, im Widerspruch zu _ABD_. Angenommen, es gelte _DCA_ statt _CDA_. Dann folgt mit (2b) zum einen _DAC_ aus
_CBD_ ˄ _BAC_ im Widerspruch zu _DCA_ und zum anderen _DAB_ aus _DCB_ ˄ _CAB_ im
Widerspruch zu _ABD_. Unter der Voraussetzung _CAB_ ˄ _ABD_
ist demnach _DCA_ nur in Kombination mit _BDC_ möglich. Werden diese vier Formeln in geeigneter Reihenfolge
hingeschrieben, nämlich: _CAB_, _ABD_, _BDC_, _DCA_, so erkennt man, dass in diesem Fall C, A, B und D zyklisch angeordnet
sind. Eine solche Anordnung der vier Punkte (abkürzend in der Formel .CABD.
zusammengefasst) auf einer Geraden widerspricht zwar der Anschauung, ist jedoch auf Grundlage der bisherigen
Axiome (noch) nicht ausgeschlossen.
Unter der Voraussetzung _CAB_ ˄ _ABD_ gilt also aufgrund der vorangegangenen Argumentation
entweder _CAD_ oder die Punkte sind gemäß der Formel .CABD. zyklisch angeordnet:
(o) _CAB_ ˄
_ABD_ ⇀ _CAD_ ⊻ .CABD.
In gleicher Weise folgt
_CAB_ ˄ _ABD_ ⇀
_DBC_ ⊻ .DBAC.
Mit .DBAC. wird dieselbe Punktanordnung beschrieben wie mit .CABD., also hat man
(*)
_CAB_ ˄ _ABD_ ⇀ _CAD_ ˄ _DBC_ ⊻ .DBAC.
Angenommen, die Punkte A, B, C und D sind gemäß der Fomel .CABD.
auf der Geraden angeordnet. Dann existiert nach II.2 ein Punkt P, so
dass P zwischen D und C liegt: _DPC_. Aus _ACD_ ˄ _CPD_ folgt wegen
(2b) _APD_;
aus _BDC_ ˄ _DPC_ folgt aus demselben Grund _BPC_.
Wenn (*) gilt, so auch gleichermaßen
(**)
_ABD_ ˄ _BDP_ ⇀ _ABP_ ˄ _ADP_ ⊻ .ABDP.
_ABP_ ˄ _ADP_ steht im Widerspruch zu _APD_, was eben abgeleitet wurde. Folglich sind die
Punkte A, B, D und P gemäß .ABDP. angeordnet und somit gilt insbesondere _PAB_.
Mit (*) hat man auch
(***)
_PCA_ ˄ _CAB_ ⇀ _PCB_ ˄
_PAB_ ⊻ .PCAB.
_PCB_ ˄ _PAB_ steht im Widerspruch zu _BPC_. Daraus folgt, dass die Punkte P, C, A und B gemäß
.PCAB. angeordnet sind. Insbesondere folgt _PBA_, im Widerspruch zu _PAB_!
Die Punkte A, B, C und D können demnach nicht gemäß der Fomel .CABD.
auf der Geraden angeordnet sein. Mit (o) folgt _CAD_.
(iv) zu zeigen: (3ab) folgt aus (1ab) und (2ab).
Mit
(1a) und (1b) bzw. (2a) und (2b) folgt
(1) _CAB_ ˄ _ABD_ ⇀ _CAD_ ˄ _CBD_
(2) _CAB_ ˄ _ADB_ ⇀ _CAD_ ˄ _CDB_
Durch Umbenennung der Punkte (B→C, C→B) erhält man aus (1) bzw. (2)
_BAC_ ˄ _ACD_ ⇀ _BAD_ ˄ _BCD_
_BAC_ ˄ _ADC_ ⇀ _BAD_ ˄ _BDC_
und hiermit die Aussagen (3a) und (3b), wenn man beachtet, dass unter der Voraussetzung _CAB_ ˄ _DAB_ weder _CAD_ noch _CBD_ möglich ist.
(v) zu zeigen: (4ab) folgt aus (2ab).
Durch Umbenennung
der Punkte (A→C, C→A bzw. B→A,
A→C, C→B) erhält man aus
(2)
_ACB_ ˄ _CDB_ ⇀ _ACD_ ˄
_ADB_
_BCA_ ˄ _CDA_ ⇀ _BCD_ ˄ _BDA_
und hiermit die Aussagen (4a) und (4b) auf ähnliche Art wie unter (iv).
Nach dem Satz von Moore ist es möglich, eine Ordnungsrelation für Punkte einer Geraden zu definieren, so dass für zwei Punkte A und B dieser Gerade entscheidbar ist, ob A vor B (A < B), bzw. B hinter A (B > A) oder aber B vor A (B < A) liegt.
Sei eine Gerade g vorgegeben. Seien ferner zwei voneinander verschiedene Punkte, O und E, auf g beliebig ausgewählt. Man lege zunächst fest, welcher von diesen beiden Punkten vor dem anderen liegen soll:
O < E.
Für einen von O und E verschiedenen Punkt A auf g gibt es nach II.3
drei sich gegenseitig ausschließende Möglichkeiten: _AOE_, _OAE_ und
_OEA_. Es wird unter Benutzung des Zeichens ⇌
(genau dann, wenn) Folgendes definiert:
A < O ⇌ _AOE_
O < A ⇌
_OAE_ oder _OEA_
A < E ⇌
_AOE_ oder _OAE_
E < A ⇌
_OEA_
Sind A und B zwei voneinander verschiedene Punkte auf g, die jeweils zudem von O bzw. E verschieden sind, so soll A < B genau dann gelten, wenn O, E, A und B auf eine der folgenden Weisen angeordnet sind: „ABOE“, „AOBE“, „AOEB“, „OABE“, „OAEB“, „OEAB“. Dagegen soll B < A genau dann gelten, wenn die Anordnung der vier Punkte von jeder der eben aufgezählten Anordnungen verschieden ist.
![]() X4
X4
Die eben definierte Ordnungsrelation < ist irreflexiv, transitiv und konnex. Mit anderen
Worten: Die Punkte auf einer Geraden sind linear geordnet.
Beweis:
Es gibt keinen Punkt A mit A < A, denn A kann
nicht verschieden von sich selbst sein. Also ist < irreflexiv.
Die beiden Fälle A < B und B < A für
zwei beliebige Punkte schließen sich nach Definition von < gegenseitig aus.
Gilt weder A < B noch B < A,
so folgt zwingend B = A. Also
ist < konnex.
Es bleibt noch die Transitivität zu zeigen. Hierzu gelte für drei kollineare Punkte A, B und C, die paarweise voneinander verschieden sind, A < B und B < C.
Fall 1: O < E und E < C.
Wegen
E < C gilt _OEC_. Wäre C < O, so
hätte man _COE_ im Widerspruch zu _OEC_. Also folgt O < C.
Fall 2: A < O und O < E.
Wegen A < O gilt _AOE_. Wäre E < A, so
hätte man _OEA_ im Widerspruch zu _AOE_. Also folgt A < E.
Fall 3: O < B und B < E.
In diesem Fall ist nichts zu zeigen.
Fall 4: A < B und B < C, wobei
A, B und C verschieden sind von O bzw. von E.
Liegt A vor B und B vor C, so ergeben sich nach obiger Definition folgende mögliche Kombinationen: „ABCOE“, „ABOCE“,
„ABOEC“, „AOBCE“, „AOBEC“, „AOEBC“, „AOEBC“, „OABCE“, „OABEC“, „OAEBC“, „OEABC“. Elimination von B liefert unter
Weglassung von Doppelnennungen die Liste „ACOE“, „AOCE“, „AOEC“, „OACE“, „OAEC“, „OEAC“, entsprechend der
Aussage A < C.
Die Tatsache, dass die Punkte auf einer Geraden linear geordnet liegen, ist weder überraschend noch erstaunlich (der Begriff „lineare Ordnung“ lautet ja nicht zufällig und ohne Grund so). Erstaunlich ist vielmehr, dass sich dieses auf Grundlage weniger und unmittelbar einleuchtender Axiome herleiten lässt.
Nach dem Vorhergehenden lassen sich irgendwelche, auf einer Geraden liegende Punkte A, B, C, ... S auf zweierlei Art anordnen:
A < B < C < ... < S oder S < ... < C < B < A.

Falls A < B < C < ..., so sagt man: „Die Punkte A, B, C, ... folgen aufeinander“.
![]() X5
X5
Zu jeder Strecke und zu jeder Geraden gehören stets unendlich viele Punkte.
Beweis:
Angenommen, zu einer beliebig vorgegebenen Strecke gehören nur endlich viele, etwa n Punkte. Dann lassen sich diese Punkte nach
X4 anordnen:
P0 < P1 < P2 < ... < Pn.
Zwischen zwei aufeinander folgenden Punkten Pi und Pi+1 gibt es gemäß II.2 noch einen weiteren Punkt P mit Pi < P < Pi+1, im Widerspruch zur Annahme.
Die Punkte auf einer Geraden liegen dicht: zwei Punkte können noch so nah nebeneinander liegen, es existiert immer ein Punkt zwischen ihnen. Aus II.2 folgt zudem, dass zu einer Geraden weder ein „größter“ noch ein „kleinster“ Punkt gehört. (Dies gilt im Übrigen auch für jede Halbgerade.)
![]() X6
X6
(i) Zu jeder Geraden gibt es einen Punkt, der nicht zu dieser
Geraden gehört.
(ii) Zu jedem Punkt gibt es eine Gerade, die
nicht durch diesen Punkt geht.
(iii) Durch jeden Punkt gehen
unendlich viele voneinander verschiedene Geraden.
Beweis:
zu (i): Diese Aussage wird mittels vollständiger Induktion
bewiesen:
Induktionsanfang:
Nach I.3 gibt es mindestens eine
Gerade, zu welcher ein Punkt existiert, der nicht zu dieser Geraden gehört.
Induktionsvoraussetzung:
Es gebe m
voneinander verschiedene Geraden, zu denen mindestens ein Punkt außerhalb
der jeweiligen Gerade existiert.
Induktionsschluss:
Seien g und h zwei von
diesen m Geraden. Wegen X5
und X1
gibt es auf g sicher einen Punkt P, der auf keiner der anderen m−1
Geraden liegt. Auf h gibt es ebenso einen Punkt Q mit der gleichen
Eigenschaft. Unter Beachtung von I.2
folgt, dass die
Gerade gPQ von jeder der m vorgegebenen Geraden verschieden
ist. Da der Schnittpunkt von g und h nicht zu gPQ gehören
kann, gibt es demnach m+1 voneinander verschiedene Geraden, zu denen
mindestens ein Punkt außerhalb der jeweiligen Gerade existiert.
zu (ii): Sei ein Punkt A beliebig vorgegeben. Sei B ein weiterer, von A verschiedener Punkt. Dann wird nach I.1 durch A und B eindeutig eine Gerade g definiert und wegen (i) gibt es einen dritten Punkt C, der nicht auf g liegt. B und C bestimmen eine zweite Gerade h. Angenommen, A liegt auf h. Dann folgt g = h und damit gehört auch C zur Geraden g. Widerspruch! Somit ist mit h eine Gerade gefunden, die nicht durch A geht.
zu (iii): Sei P irgendein Punkt. Dann gibt es wegen (ii) eine Gerade, die nicht durch P geht. Diese sei etwa mit g bezeichnet. Dann wird aufgrund von I.1 zusammen mit P durch jeden Punkt auf g eindeutig je eine Gerade definiert. Seien nun S und T zwei voneinander verschiedene Punkte auf g. Angenommen, die Geraden gPS und gPT sind identisch. Dann folgt gPS = g und somit liegt P auf g. Widerspruch, denn nach Voraussetzung geht g nicht durch P. Demnach sind die Geraden gPS und gPT verschieden voneinander. Also folgt die behauptete Aussage, denn nach X5 liegen auf g unendlich viele Punkte.
Sei gOE eine Gerade mit O < E. Diese Gerade wird zerlegt in zwei von O ausgehende Halbgeraden (oder: Strahlen). Zur einen Halbgerade gehören alle Punkte P auf gOE mit P > O, zur anderen Halbgeraden gehören alle Punkte P mit P < O. Jeder Punkt auf gOE ist also entweder gleich O oder gehört zu einer der beiden Halbgeraden. Sind P und Q Punkte derselben Halbgerade, so liegt O nicht zwischen P und Q.
Ist h eine von O ausgehende Halbgerade und T irgendein Punkt auf h, so soll diese Halbgerade mit OT>, die andere von O ausgehende Halbgerade soll mit <OT bezeichnet werden. <OT heißt die zu OT> entgegengesetzte Halbgerade.
Gegeben sei eine Gerade g und zwei Punkte A und B, die nicht auf g liegen. Wenn AB und g einen gemeinsamen Punkt haben, so sagt man, dass A und B auf verschiedenen Seiten von g liegen; falls dagegen AB von g nicht geschnitten wird, so sagt man, dass A und B auf derselben Seite von g liegen.
![]() X7
X7
Jede Gerade hat genau zwei Seiten.

Beweis:
Sei g eine Gerade und O ein Punkt, der auf g liegt, sowie A ein Punkt, der nicht auf g liegt. Dann existiert
wegen II.2 ein dritter Punkt B, so dass O zwischen A und B liegt.
A und B liegen somit auf zwei verschiedenen Seiten von g. Sei nun P ein von A und B verschiedener Punkt, der nicht
zu g gehört, aber ansonsten beliebig gewählt ist.
Sind A, B und P keine kollinearen Punkte, so gibt es nach dem Axiom von Pasch für P genau zwei Möglichkeiten: Entweder wird die Strecke PA oder die Strecke PB von g geschnitten. Angenommen, g schneidet PB. Dann wird PA nicht von g geschnitten und A und P liegen auf derselben Seite auf g. Wird dagegen PA von g geschnitten, so wird PB nicht von g geschnitten und B und P liegen auf derselben Seite von g.
Sind A, B und P kollinear, so liegen A, B, O und P auf ein und derselben Geraden. Dann liegt P entweder auf der Halbgeraden OA> und damit auf derselben Seite von g wie A oder auf OB> und damit auf derselben Seite von g wie B.
Abgesehen von II.2 folgt der Satz, dass jede Gerade genau zwei Seiten hat, im Wesentlichen aus dem Axiom von Pasch. Umgekehrt folgt aus X7 die Aussage des Axioms von Pasch. Ist nämlich ein Dreieck ABC gegeben, das in mindestens einer Seite (etwa AB) von einer Geraden g geschnitten wird, so gibt es unter der Voraussetzung, dass X7 gültig ist, für den dritten Punkt C genau zwei verschiedene Möglichkeiten: Entweder er liegt zusammen mit A auf einer der beiden Seiten von g oder zusammen mit B auf der anderen Seite. Im ersten Fall schneidet g BC, aber nicht AC, im zweiten Fall schneidet g AC, aber nicht BC.
Ein Streckenzug ABC...N besteht aus den Strecken AB, BC, CD, ... MN. Fällt der letzte Punkt mit dem ersten Punkt eines Streckenzugs zusammen, so wird dieser Streckenzug Polygon genannt. AB, BC, ... heißen dann die Seiten des Polygons; A, B, ... sind die Eckpunkte (oder kurz: Ecken) des Polygons.
Sind die Ecken eines Polygons paarweise verschieden voneinander, gehört kein Eckpunkt des Polygons zu einer seiner Seiten und haben jeweils zwei der Seiten keinen gemeinsamen Punkt, so handelt es sich um ein einfaches Polygon. Einfache Polygone mit 3, 4, ..., n Ecken heißen Dreiecke, Vierecke, ... bzw. n-Ecke.
Wird aus (beliebig vielen) Punkten, die auf derselben Seite einer Geraden liegen, ein Streckenzug gebildet, so befindet sich dieser Streckenzug komplett auf eben dieser Seite. Wird dagegen (mindestens) eine Seite eines Streckenzuges von g geschnitten, so gibt es nach X7 mindestens zwei Punkte dieses Streckenzugs, die sich auf verschiedenen Seiten von g befinden.
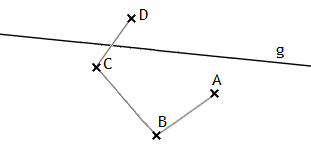
Lineare Kongruenzaxiome
![]() III.1. Seien A und B Punkte auf einer Geraden und h eine von einem beliebigen
Punkt A’ ausgehende Halbgerade. Dann gibt es genau einen Punkt B’ auf h, so dass
AB kongruent zu A’B’ ist, in Zeichen:
III.1. Seien A und B Punkte auf einer Geraden und h eine von einem beliebigen
Punkt A’ ausgehende Halbgerade. Dann gibt es genau einen Punkt B’ auf h, so dass
AB kongruent zu A’B’ ist, in Zeichen:
AB ≡ A’B’.
![]() III.2. Ist eine Strecke
AB sowohl zu A’B’
als auch zu A’’B’’
kongruent, so ist auch A’B’ kongruent zu A’’B’’,
formal geschrieben:
III.2. Ist eine Strecke
AB sowohl zu A’B’
als auch zu A’’B’’
kongruent, so ist auch A’B’ kongruent zu A’’B’’,
formal geschrieben:
AB ≡ A’B’ und AB ≡ A’’B’’ ⇀
A’B’ ≡ A’’B’’.
![]() III.3. Es seien
AB und BC zwei Strecken ohne gemeinsame Punkte auf einer
Geraden g. Seien ferner A’B’ und B’C’
zwei Strecken auf derselben oder einer anderen Geraden g’, ebenfalls ohne gemeinsame Punkte. Dann gilt
III.3. Es seien
AB und BC zwei Strecken ohne gemeinsame Punkte auf einer
Geraden g. Seien ferner A’B’ und B’C’
zwei Strecken auf derselben oder einer anderen Geraden g’, ebenfalls ohne gemeinsame Punkte. Dann gilt
AB ≡ A’B’
und BC ≡ B’C’ ⇀
AC ≡ A’C’.
Axiom III.1 besagt in alternativer Sprechweise, dass eine gegebene Strecke von einem beliebigen Punkt aus auf einer von diesem Punkt ausgehenden Halbgeraden in eindeutiger Weise abgetragen werden kann.
![]() X8
X8
≡ („ist kongruent zu“) ist reflexiv, symmetrisch und transitiv.
Beweis:
zu zeigen: Reflexivität.
Es darf nach III.1 als A’ insbesondere A gewählt
werden. Dann ist B’ bereits gefunden: es ist B’ = B. Also gilt
AB ≡ BA,
mit anderen Worten: jede Strecke ist zu sich selbst kongruent.
zu zeigen: Symmetrie.
Wegen der Reflexivität von ≡ hat man mit III.2
AB ≡ A’B’ und
AB ≡ AB ⇀
A’B’ ≡ AB.
zu zeigen: Transitivität.
Wegen der Symmetrie von ≡ ist
AB ≡ A’B’
gleichbedeutend mit A’B’ ≡
AB. Wiederum mit III.2 hat man
A’B’ ≡
AB und
AB ≡ A’’B’’ ⇀
A’B’ ≡ A’’B’’
und damit die Transitivität von ≡.
Wegen der Symmetrie von ≡ bedeutet „AB ≡ CD“ fortan nicht mehr nur „AB ist kongruent zu CD“, sondern: „AB und CD sind zueinander kongruent“.
Es seien AB und CD zwei beliebige Strecken. Dann ist der Punkt E auf der Halbgeraden AB> mit BE ≡ CD und _ABE_ nach III.1 eindeutig bestimmt. AE heißt die Summe von AB und CD.
AB + CD =def AE
Man sagt, „AE entsteht durch Verlängerung von AB mit CD“ oder „Wenn man AB mit CD verlängert, so erhält man AE“.
Obwohl AB = BA bzw. CD = DC gilt, sind die Summen AB + CD und BA + DC nicht identisch!
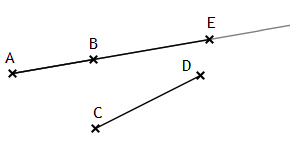
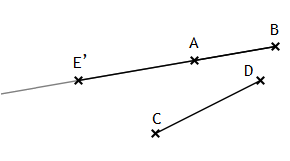
AB + CD =
AE,
BA + DC =
BE’
Allerdings folgt mit III.2 und III.3, dass AE ≡ BE’. In gleicher Weise ergibt sich die Aussage des nächsten Satzes:
![]() X9
X9
Ist AB ≡ A’B’ und CD ≡
C’D’, so folgt AB + CD
≡ A’B’+ C’D’.
![]() X10
X10
Seien A, B, C sowie D, E, F jeweils kollineare Punkte. B liege zwischen A und C und es gelte
AB ≡ DE
und AC ≡ DF.
Dann liegt E zwischen D und F und es gilt BC ≡ EF.
Beweis:
Auf der Halbgeraden DE> kann ein Punkt F’ so gewählt werden,
dass einerseits _DEF’_ (nach II.2)
und andererseits EF’ ≡ BC
(nach III.1) ist. Dann folgt mit III.3
AC ≡ DF’.
Da nach Voraussetzung auch AC ≡ DF
gilt, muss wegen III.1 F’ mit F identisch sein. Demzufolge gilt ebenfalls _DEF_.
Es seien A, B, C kollineare Punkte und B liege zwischen A und C. Dann heißt BC die Differenz von AC und AB.
AC − AB =def BC
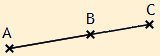
Eine Strecke AB heißt genau dann kleiner als eine andere Strecke CD (bzw. CD größer als AB), in Zeichen:
AB < CD,
wenn zur Strecke CD ein Punkt P gehört, so dass AB ≡ CP gilt.
![]() X11
X11
Ist AB ≡ A’B’
und CD ≡ C’D’,
so folgt
AB < CD
⇌ A’B’ < C’D’
Beweis:
Sei AB < CD. Dann existiert nach Definition
ein Punkt E mit _CED_ und AB ≡ CE.
Nach III.1 gibt es somit auf der Halbgeraden C’D’> genau einen Punkt E’, so dass
CE ≡ C’E’.
Zusammen mit CD ≡ C’D’
folgt wegen X10, dass E’ zwischen C’ und D’ liegt. Zudem hat man
A’B’ ≡ AB ≡ CE ≡ C’E’.
Wegen der Transitivität von ≡ folgt A’B’ ≡ C’E’ und hiermit A’B’ < C’D’.
A’B’ < C’D’ ⇀ AB
< CD zeigt man auf genau dieselbe Weise.
![]() X12
X12
Ist AB < CD und
CD < EF,
so gilt auch AB < EF.
Beweis:
Aus AB < CD
folgt nach Definition, dass es einen Punkt P zwischen C und D gibt, für
den AB ≡ CP
gilt. CD < EF
bedeutet für einen Punkt Q zwischen E und F, dass CD ≡ EQ.
Nach X10 gibt es dann einen Punkt R
zwischen E und Q mit CP ≡ ER.
Wegen AB ≡ CP
gilt somit auch AB ≡ ER.
Aus _EQF_ und _ERQ_ ergibt sich wegen X3, dass für die Punkte E, Q, R und F nur die Anordnungen „ERQF“ und „FQRE“ möglich sind. In jedem Fall bedeutet dies _ERF_ und damit folgt AB < EF.
![]() X13
X13
Für zwei beliebige Strecken AB und CD gilt genau eine der
folgenden Möglichkeiten: AB < CD,
AB ≡ CD,
CD < AB.
Beweis:
Sei ein Punkt P auf der Halbgeraden CD> so gewählt, dass
AB ≡ CE.
Dann trifft wegen II.3 nur
genau eine der folgenden Möglichkeiten zu: _CED_ (in diesem Fall
gilt AB < CD),
_CDE_ (dies bedeutet CD < AB),
E = D (was gleichbedeutend ist mit
AB ≡ CD).
Durch zwei von einem Punkt V ausgehende Halbgeraden h und k, die zwei verschiedenen Geraden angehören, wird ein Winkel definiert, der mit ∠(h,k) oder mit ∠(k,h) bezeichnet wird. h und k heißen Schenkel dieses Winkels; V wird Scheitel dieses Winkels genannt. Mit jedem Winkel ∠(h,k) gibt es ein bestimmtes Teilgebiet der Ebene, das wie folgt charakterisiert ist: Seien A und B Punkte, die in diesem Teilgebiet liegen, aber ansonsten beliebig gewählt sind. Dann wird die Strecke AB stets weder von h noch von k geschnitten. Dieses Teilgebiet heißt das Innere des Winkels ∠(h,k). Die Punkte im Inneren eines Winkels heißen innere Punkte.
Ist H ein Punkt auf h, K ein Punkt auf k und V der Scheitel des Winkels ∠(h,k), so kann dieser auch mit ∠HVK oder mit ∠KVH bezeichnet werden.
Zudem ist es allgemein üblich, Winkel auch mit griechischen Kleinbuchstaben zu bezeichnen.

Ebene Kongruenzaxiome
![]() III.4. Seien ein Winkel ∠(h,k) sowie eine von einem Punkt
V’
ausgehende Halbgerade h’ auf einer Geraden g’ gegeben. Man wähle nun eine der beiden Seiten von g’ aus. Dann gibt es auf
dieser Seite von g’ genau eine von V’ ausgehende Halbgerade k’, so
dass ∠(h,k) kongruent ist zu ∠(h’,k’)
und zugleich alle inneren Punkte von ∠(h’,k’)
auf der gewählten Seite von g’ liegen, in Zeichen:
III.4. Seien ein Winkel ∠(h,k) sowie eine von einem Punkt
V’
ausgehende Halbgerade h’ auf einer Geraden g’ gegeben. Man wähle nun eine der beiden Seiten von g’ aus. Dann gibt es auf
dieser Seite von g’ genau eine von V’ ausgehende Halbgerade k’, so
dass ∠(h,k) kongruent ist zu ∠(h’,k’)
und zugleich alle inneren Punkte von ∠(h’,k’)
auf der gewählten Seite von g’ liegen, in Zeichen:
∠(h,k) ≚ ∠(h’,k’).
Jeder Winkel ist zu sich selbst kongruent. Das heißt, es ist stets
∠(h,k) ≚ ∠(h,k) und ∠(h,k) ≚ ∠(k,h).
![]() III.5. Ist ein Winkel
∠(h,k) sowohl zu ∠(h’,k’)
als auch zu ∠(h’’,k’’) kongruent, so ist auch
∠(h’,k’) kongruent zu ∠(h’’,k’’),
formal geschrieben:
III.5. Ist ein Winkel
∠(h,k) sowohl zu ∠(h’,k’)
als auch zu ∠(h’’,k’’) kongruent, so ist auch
∠(h’,k’) kongruent zu ∠(h’’,k’’),
formal geschrieben:
∠(h,k) ≚ ∠(h’,k’) und
∠(h,k) ≚ ∠(h’’,k’’) ⇀
∠(h’,k’) ≚ ∠(h’’,k’’).
![]() III.6. Gelten für die Dreiecke ABC und A’B’C’ die Kongruenzen
III.6. Gelten für die Dreiecke ABC und A’B’C’ die Kongruenzen
AB ≡ A’B’, AC ≡ A’C’ und ∠BAC ≚ ∠B’A’C’,
so gilt auch
∠ABC ≚ ∠A’B’C’ und ∠ACB ≚ ∠A’C’B’.
Axiom III.4 besagt in alternativer Sprechweise, dass ein gegebener Winkel nach einer gegebenen Seite an einer gegebenen Halbgeraden auf eindeutig bestimmte Weise abgetragen werden kann.
So wie ≡ ist auch ≚ reflexiv, symmetrisch und transitiv. (vgl. X8)
Gegeben seien zwei Winkel, die denselben Scheitel und einen gemeinsamen Schenkel haben. Wenn deren nicht gemeinsame Schenkel auf einer Geraden liegen, heißen diese Winkel Nebenwinkel.
Zwei Winkel mit gemeinsamem Scheitel, deren Schenkel je eine Gerade bilden, heißen Scheitelwinkel.
Ein Winkel, der zu einem seiner Nebenwinkel kongruent ist, heißt ein rechter Winkel (oder kurz: ein Rechter).
Der letzte Satz legt zwar fest, was unter einem rechten Winkel verstanden werden soll, macht aber keine Aussage darüber, ob ein solcher Winkel überhaupt existiert (siehe aber X21: Es gibt rechte Winkel).
Zwei Dreiecke ABC und A’B’C’ heißen zueinander kongruent (in Zeichen: ABC ≅ A’B’C’), wenn
AB ≡ A’B’, BC ≡
B’C’, CA ≡ C’A’
und
∠A ≚ ∠A’,
∠B ≚ ∠B’,
∠C ≚ ∠C’
gilt. Hierbei ist ∠A eine abkürzende Schreibweise für ∠BAC (bzw. ∠B für ∠ABC und ∠C für ∠ACB). ∠A nennt man „den von AB und AC eingeschlossenen Winkel“; ∠B und ∠C werden entsprechend bezeichnet.
![]() X14
(Kongruenzsatz „sws“)
X14
(Kongruenzsatz „sws“)
Wenn für zwei Dreiecke ABC und A’B’C’
AB ≡ A’B’, AC ≡ A’C’ und ∠A ≚ ∠A’
gilt, so sind beide Dreiecke zueinander kongruent.
[vgl. Euklid I.§4]
Beweis:
∠B ≚
∠B’ bzw. ∠C ≚
∠C’ folgt bereits aus III.6.
Bleibt zu zeigen:
BC ≡ B’C’.
Angenommen, BC und B’C’ sind nicht kongruent. Dann gibt es wegen III.1 den
Punkt D’auf A’C’> mit
BC ≡ B’D’.
Hieraus folgt zusammen mit AB ≡ A’B’ und
∠B ≚ ∠B’
wegen III.6 insbesondere, dass
∠BAC ≚ ∠B’A’D’.
Nach Voraussetzung gilt auch
∠BAC ≚ ∠B’A’C’.
Dies bedeutet aber, dass der Winkel
∠BAC auf zweierlei Art an der Halbgeraden
A’B’> abgetragen werden kann, im Widerspruch zu III.4.
![]() X15
(Kongruenzsatz „wsw“)
X15
(Kongruenzsatz „wsw“)
Wenn für zwei Dreiecke ABC und A’B’C’
∠A ≚ ∠A’, ∠B ≚ ∠B’ und AB ≡ A’B’
gilt, so sind beide Dreiecke zueinander kongruent.
[vgl. Euklid I.§26]
Beweis:
Sei ∠A ≚
∠A’, ∠B ≚
∠B’ und
AB ≡ A’B’.
Wegen III.1 gibt es den Punkt D’auf A’C’> mit
AC ≡ A’D’.
Mit X14 folgt ABC ≅ A’B’D’ und
damit insbesondere
∠B ≚ ∠A’B’D’.
Nach Voraussetzung ist aber
∠B ≚ ∠B’,
also gilt
∠A’B’C’ ≚ ∠A’B’D’.
Nach III.4
müssen C’ und D’ auf ein und derselben, von B’ ausgehenden Halbgerade liegen. Andererseits liegen C’ und D’ beide auf der
Halbgeraden A’C’>.
Wegen X1 folgt C’ = D’
und somit AC ≡ A’C’.
Mit X14 folgt die Behauptung.
![]() X16
X16
Wenn zwei Winkel zueinander kongruent sind, so sind auch ihre Nebenwinkel kongruent zueinander.
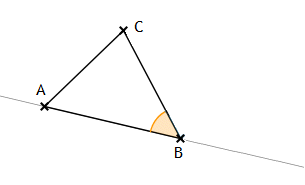

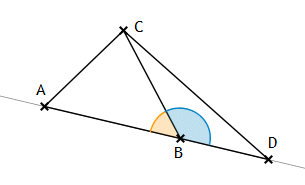
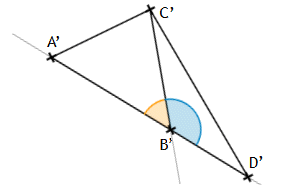
Beweis:
Gegeben sei ein beliebiges Dreieck ABC und ein Punkt B’ auf einer beliebigen Geraden h. Für zwei von B’ ausgehende
Halbgeraden h’ und k’ sei
∠(h’,k’) ≚ ∠ABC
vorausgesetzt, wobei h’ zu h gehören soll. Man wähle nun einen Punkt D auf der Geraden
gAB, so dass
B zwischen A und D liegt. Dann gibt es wegen
III.4 die Punkte A’ auf h’ bzw.
C’ auf k’ sowie danach D’ auf h mit _A’B’D’_, so dass
B’A’ ≡ BA,
B’C’ ≡ BC
und B’D’ ≡ BD.
Gemäß Voraussetzung ist
∠A’B’C’ ≚ ∠ABC.
Also gilt wegen X14 A’B’C ≅ ABC
und damit
∠B’A’C’ ≚ ∠BAC und
A’C’ ≡ AC.
Nach Axiom III.3 ist auch
A’D’ ≡ AD.
Somit folgt wiederum mit X14, dass
die Dreiecke A’D’C’ und ADC zueinander kongruent sind, was insbesondere
C’D’ ≡ CD
und ∠A’D’C’ ≚ ∠ADC bedeutet. Zusammen mit
B’D’ ≡ BD
folgt schließlich unter Anwendung von III.6, dass die Winkel ∠D’B’C’
und ∠DBC kongruent zueinander sind, was zu
zeigen war.
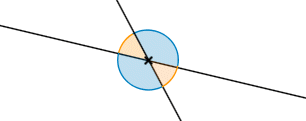
Aus X16 folgt unmittelbar der nächste Satz:
![]() X17
X17
Scheitelwinkel sind stets kongruent zueinander.
[vgl. Euklid I.§15]
![]() X18
(Crossbar-Theorem)
X18
(Crossbar-Theorem)
Es seien A, B und C drei nicht in gerader Linie
gelegene Punkte und P ein beliebiger Punkt im Inneren des Winkels ∠CAB.
Dann hat die Halbgerade AP> mit der Strecke BC
einen Punkt gemeinsam.
Beweis:
Nach II.2 gibt
es einen Punkt D auf der Geraden gAB mit _DAB_. gAP schneidet somit die Seite
DB des Dreiecks DBC, weswegen gAP nach dem Axiom von Pasch auch entweder
BC oder DC schneidet.
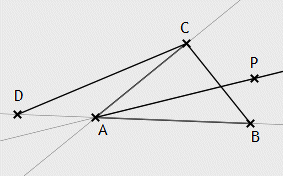
zu zeigen: gAP schneidet DC nicht.
Alle zur Strecke DC gehörenden Punkte liegen auf einer Seite von
gAC, und zwar auf
derjenigen Seite von gAC, auf welcher B nicht liegt (weil D und B wegen _DAB_ auf verschiedenen
Seiten von gAC liegen).
Alle Punkte der Halbgeraden AP> liegen im Inneren von ∠CAB und damit auf derjenigen Seite von gAC, auf welcher B liegt. Demnach kann keiner der Punkte von AP> zu DC gehören.
Alle Punkte der zu AP> entgegengesetzten Halbgeraden liegen nicht auf derjenigen Seite von gDB, auf welcher die Punkte von DC liegen. Also haben auch <AP und DC keinen gemeinsamen Punkt.
Der gemeinsame Punkt S von gAP und BC liegt auf AP>, denn sowohl C und S als auch C und P liegen auf derselben Seite von gAB, also auch P und S.
![]() X19
X19
Gegeben seien zwei zueinander kongruente Winkel
∠(h,k) und ∠(h’,k’).
Sei l eine vom Scheitel des Winkels ∠(h,k) ausgehende Halbgerade, die
im Inneren dieses Winkels verläuft. Dann gibt es stets eine Halbgerade l’, die vom Scheitel des Winkels
∠(h’,k’) ausgeht und im Inneren dieses Winkels verläuft, so dass Folgendes gilt:
∠(h,l) ≚ ∠(h’,l’) und ∠(k,l) ≚ ∠(k’,l’).
Beweis:
Die Scheitel von ∠(h,k) bzw. von ∠(h’,k’)
seien mit V bzw. V’ bezeichnet. Auf den Schenkeln h, k, h’ und k’ lassen
sich Punkte A, B, A’ und B’ wegen III.1 so wählen, dass
VA ≡ V’A’
und VB ≡ V’B’
gilt. Zusammen mit ∠(h,k) ≚ ∠(h’,k’)
folgt, dass die Dreiecke VAB und V’A’B’ zueinander kongruent sind. Demnach
gilt ∠VAB ≚ ∠V’A’B’
und ∠VBA ≚ ∠V’B’A’
sowie AB ≡ A’B’.
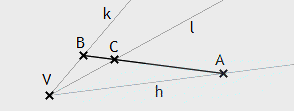
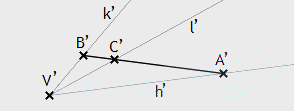
Da l nach Voraussetzung im Inneren von ∠(h,k) verläuft, muss es nach X18 einen Punkt geben, in dem sich l und AB schneiden. Dieser Schnittpunkt soll mit C bezeichnet werden. Sei nun C’ derjenige Punkt auf A’B’, so dass A’B’ ≡ AC. Weil AB ≡ A’B’ gilt, folgt unter Verwendung von III.3 auch B’C’ ≡ BC. Wegen X10 liegt C’ somit zwischen B’ und A’. Die von V’ ausgehende und durch C’ verlaufende, mit l’ bezeichnete Halbgerade liegt also im Inneren von ∠(h’,k’). Ferner folgen mit X14 die Kongruenzen VAC ≅ V’A’C’ sowie VBC ≅ V’B’C’ und damit ergibt sich schließlich die zu beweisende Aussage.
![]() X20
X20
Gegeben seien zwei Winkel ∠(h,k)
und
∠(h’,k’). Ferner seien l
und l’
zwei von den Scheiteln dieser Winkel ausgehende Halbgeraden und zwar derart, dass l im Inneren von
∠(h,k) bzw. l’ im Inneren von
∠(h’,k’) verläuft. Falls
dann ∠(h,l) ≚ ∠(h’,l’)
und ∠(k,l) ≚ ∠(k’,l’) gilt, so auch
∠(h,k) ≚ ∠(h’,k’).
Im Fall, dass
∠(h,k) ≚ ∠(h’,k’)
und
∠(h,l) ≚ ∠(h’,l’),
folgt
∠(k,l) ≚ ∠(k’,l’).
Beweis:
Die Scheitel von ∠(h,k) bzw. von ∠(h’,k’)
seien mit V bzw. V’ bezeichnet. A auf h, B auf k, C auf l, A’ auf h’, B’
auf k’, C’ auf l’ seien so gewählt, dass VA ≡ V’A’, VB ≡ V’B’,
VC ≡ V’C’
und dass C zwischen A und B bzw. C’ zwischen A’ und B’ liegt.


Wenn ∠(h,l) ≚ ∠(h’,l’) und ∠(k,l) ≚ ∠(k’,l’) gilt, so folgt mit dem Kongruenzsatz sws VAC ≅ V’A’C’ sowie VCB ≅ V’C’B’. Also gilt sowohl AC ≡ A’C’ und BC ≡ B’C’ (und damit wegen III.3 AB ≡ A’B’) als auch ∠VAB ≚ ∠V’A’B’ und ∠VBA ≚ ∠V’B’A’. Mit dem Kongruenzsatz wsw folgt VAB ≅ V’A’B’ und hiermit ∠BVA ≚ ∠B’V’A’.
Die zweite Aussage lässt sich auf ganz ähnliche Art beweisen.
Nach X20 ist nunmehr die folgende Definition sinnvoll:
Gegeben sei ein Winkel ∠(h,k) und eine vom Scheitel dieses Winkels ausgehende Halbgerade, wobei l im Inneren von ∠(h,k) verlaufen soll. Dann heißt ∠(l,k) die Differenz von ∠(h,k) und ∠(h,l) und ∠(h,k) die Summe von ∠(h,l) und ∠(l,k).
∠(h,k) −
∠(h,l) =def ∠(l,k)
∠(h,l) + ∠(l,k) =def ∠(h,k)
Die Bestandteile einer Winkelsumme sind gemäß dieser Definition zusammengefügte Winkel, das heißt Winkel, die einen gemeinsamen Schenkel und denselben Scheitel besitzen. Falls ∠(h,l) + ∠(l,k) = ∠(h,k) gilt, so sagt man, „∠(h,k) entsteht durch Erweiterung von ∠(h,l) mit ∠(l,k)“ oder „Wenn man ∠(h,l) mit ∠(l,k) erweitert, so erhält man ∠(h,k)“.
Seien ∠(h,l) und ∠(l,k) zwei zusammengefügte Winkel mit ∠(h,l) + ∠(l,k) = ∠(h,k). Wenn es dann zwei nicht-zusammengefügte Winkel ∠(r,s) und ∠(r’,s’) gibt mit ∠(h,l) ≚ ∠(r,s) und ∠(l,k) ≚ ∠(r’,s’), so sagt man auch: „∠(h,k) ist gleich der Summe von ∠(r,s) und ∠(r’,s’)“ oder „Die Summe von ∠(r,s) und ∠(r’,s’) ist gleich ∠(h,k)“.
Ein Winkel ∠AVB heißt genau dann kleiner als ein anderer Winkel ∠CWD, (in Zeichen: ∠AVB < ∠CWD), wenn es im Inneren des Winkels ∠CWD einen Punkt P gibt, so dass ∠AVB ≚ ∠CWP gilt.
Anders gesagt: Ein Winkel κ ist genau dann kleiner als ein anderer Winkel γ, wenn es einen Winkel δ gibt, so dass κ + δ = γ.
![]() X21
X21
Es gibt rechte Winkel.
Beweis:
Sei h eine vom Punkt V ausgehende Halbgerade. Nach III.4 gibt
es zwei weitere von V ausgehende Halbgeraden k und l mit
∠(k,h) ≚ ∠(l,h).
Nach III.1 kann man dann
Punkte A auf k und B auf l so festlegen, dass VA ≡ VB.
Wegen X18
wird die Strecke AB von h geschnitten, etwa im Punkt S.
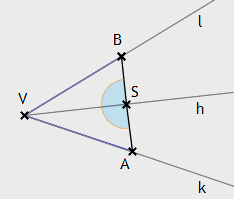
Die Dreiecke VAS und VBS sind wegen sws kongruent zueinander. Es folgt also
∠ASV ≚ ∠BSV.
Diese beiden Winkel sind gleichzeitig Nebenwinkel und somit nach Definition auch rechte Winkel.
![]() X22
X22
Alle rechten Winkel sind zueinander kongruent.
Beweis:
Seien der Winkel ∠BAD und sein
Nebenwinkel ∠CAD bzw. der Winkel ∠B’A’D’
und dessen Nebenwinkel ∠C’A’D’
zueinander kongruent. Dann ist jeder dieser vier Winkel ein rechter Winkel.
Angenommen, es gilt ∠B’A’D’ ≚ ∠BAD nicht. Der Winkel ∠B’A’D’ soll nun an der Halbgeraden AB> abgetragen werden, und zwar nach derjenigen Seite von gBC, auf welcher D liegt. Dann befindet sich der hierdurch entstehende Schenkel h im Inneren entweder von ∠BAD oder von ∠CAD. Es ist möglich, etwa den ersten dieser zwei Fälle anzunehmen (denn im zweiten Fall kann man die folgende Argumentation in gleicher Weise führen). Es befinde sich also AD* auf h mit AD* ≡ A’D’ im Inneren von ∠BAD.

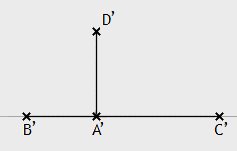
Weil die Winkel ∠B’A’D’ und ∠BAD* zueinander kongruent sind, gilt nach X16 das Gleiche auch für deren Nebenwinkel, also ∠C’A’D’ ≚ ∠CAD*. Andererseits hat man nach Voraussetzung ∠C’A’D’ ≚ ∠B’A’D’. Zusammen mit ∠B’A’D’ ≚ ∠BAD* folgt wegen III.5
(*) ∠BAD* ≚ ∠CAD*.
Nach Voraussetzung ist ∠BAD ≚ ∠CAD. Nach X19 gibt es demnach im Inneren von ∠CAD eine Halbgerade AD^> mit AD^ ≡ AD*, für die insbesondere
(**) ∠BAD* ≚ ∠CAD^
gilt. Wiederum mit III.5 folgt aus (*) und (**), dass ∠CAD* ≚ ∠CAD^. Da nach III.1 jeder Winkel an eine gegebenen Halbgerade nach einer gegebenen Seite nur auf genau eine Weise abgetragen werden kann, folgt D* = D^ und damit ein Widerspruch, denn D* und D^ liegen auf verschiedenen Seiten von gAD.
Das 4. Postulat von Euklid, welches besagt, dass „alle rechten Winkel einander gleich sind“, hat sich damit als unnötig erwiesen.
Seien B und C Punkte auf einer beliebigen Geraden g , A ein Punkt zwischen B und C und D ein Punkt, der nicht zu g gehört. Seien ferner ∠BAD bzw. ∠CAD rechte Winkel. Sei die von A ausgehende Halbgerade auf g mit g* bezeichnet. Liegt die von A ausgehende Halbgerade h im Inneren von ∠CAD, so ist ∠(g*,h) ein spitzer Winkel, liegt h dagegen im Inneren von ∠BAD, so ist ∠(g*,h) ein stumpfer Winkel.
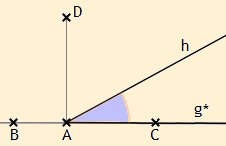
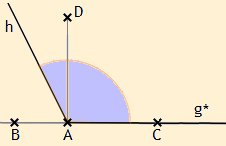
Durch das Zusammenfügen zweier rechter Winkel oder gar zweier stumpfer Winkel ergeben sich keine Winkel, denn in der Theorie der ebenen Geometrie nach Hilbert gibt es weder überstumpfe noch gestreckte Winkel. Allerdings sind (seit Euklid) folgende Sprechweisen üblich:
Werden zwei oder auch mehrere Winkel nacheinander zusammengefügt und liegen diejenigen zwei Schenkel, die jeweils nur zu einem Winkel gehören, auf ein und derselben Geraden, so sagt man beispielsweise: „Diese Winkel entsprechen zusammen zwei rechten Winkeln“ oder „Diese Winkel sind zusammen zwei Rechten gleich“ oder „Diese Winkel ergeben zusammen zwei Rechte“.
Zwei Nebenwinkel, die nach Definition bereits zusammengefügt sind, entsprechen immer zwei Rechten. Aus diesem Grund sind bei gegebenen Nebenwinkeln entweder beide rechte Winkel oder aber einer von beiden ist spitz, der andere stumpf.
![]() X23
(Basiswinkelsatz)
X23
(Basiswinkelsatz)
Sind in einem Dreieck ABC
die Seiten AC und BC
kongruent zueinander, so gilt
∠A ≚ ∠B.
[vgl. Euklid I.§5]
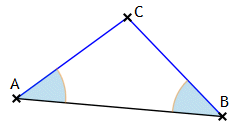
Beweis:
Aus AC ≡ BC
folgt ∠A ≚ ∠B
unmittelbar durch Anwendung von III.6
auf die Dreiecke ABC und BAC.
Ein Dreieck ABC mit AC ≡ BC heißt gleichschenklig. Die Seite AB eines gleichschenkligen Dreiecks heißt Basis (oder Grundseite), die zueinander kongruenten Winkel ∠A und ∠B werden Basiswinkel genannt.
![]() X24
(Umkehrung von X23)
X24
(Umkehrung von X23)
Sind in einem Dreieck ABC
die Winkel ∠A und ∠B
kongruent zueinander, so gilt
AC ≡ BC.
[vgl. Euklid I.§6]
Beweis:
Es gelte in einem Dreieck ABC
∠CAB ≚ ∠CBA.
Angenommen, die Seiten AC und BC
sind nicht kongruent zueinander. Dann kann man nach X13
annehmen, dass AC < BC
gilt. (Im Fall BC < AC
könnte nachfolgend in gleicher Weise argumentiert werden.) Unter der Annahme
AC < BC
gibt es einen Punkt D zwischen B und C, so dass
AC ≡ BD.
Zusammen mit ∠A ≚ ∠B
folgt wegen III.6, dass die Dreiecke BCD und CBA kongruent zueinander sind und damit
∠DAB ≚ ∠CBA.
Also gilt mit
∠CAB ≚ ∠CBA auch
∠DAB ≚ ∠CAB.
C und D liegen auf derselben Seite von gAB. Demnach folgt aus
∠DAB ≚ ∠CAB wegen
III.4,
dass die Halbgeraden AC> und AD> identisch sein müssen bzw. dass A, D und
C kollineare Punkte sind. Weil D ein Punkt der Strecke BC
ist, ergibt sich schließlich die Kollinearität der Punkte A, B und C. Dies
steht im Widerspruch zur Voraussetzung: ABC ist als Dreieck definiert.
![]() X25
(Kongruenzsatz „sss“)
X25
(Kongruenzsatz „sss“)
Wenn für zwei Dreiecke ABC und A’B’C’
AB ≡ A’B’, BC ≡ B’C’ und CA ≡ C’A’
gilt, so sind beide Dreiecke zueinander kongruent.
[vgl. Euklid I.§8]
Beweis:
Der Winkel ∠A wird an der Halbgeraden A’B’>
abgetragen, und zwar nach der Seite, auf welcher C’ nicht liegt. Auf der so entstehenden Halbgeraden gibt es den Punkt
C’’ mit A’C’’ ≡ AC.
Wegen des Kongruenzsatzes sws folgt
(*) ABC ≅ A’B’C’’
und hiermit B’C’’ ≡ BC. Unter Beachtung von BC ≡ B’C’ und CA ≡ C’A’ folgt die Gleichschenkligkeit der Dreiecke C’C’’B’ und C’’C’A’.
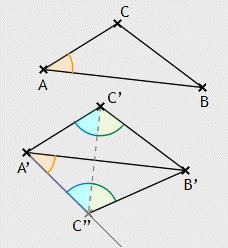
Wegen X23 in Verbindung mit X20 hat man ∠A’C’’B’ ≚ ∠A’C’B’ und hiermit auch A’B’C’’ ≅ A’B’C’. Mit (*) folgt die Behauptung.
Eine Ebene, in der die ebenen Inzidenzaxiome (I.1 bis I.3), die linearen Anordnungsaxiome (II.1 bis II.3), das Axiom von Pasch (II.4), die linearen Kongruenzaxiome (III.1 bis III.3) sowie die ebenen Kongruenzaxiome (III.4 bis III.6) gelten, heißt Hilbertebene.
Viele bekannte elementargeometrische Sätze (insbesondere solche aus der Dreiecksgeometrie) lassen sich bereits in einer Hilbertebene beweisen. Einige dieser Sätze sind Gegenstand dieses Abschnitts.
![]() X26
X26
Jede Strecke kann Basis eines gleichschenkligen Dreiecks sein.
[vgl. Euklid I.§1]
Beweis:
Sei die Strecke AB beliebig
gewählt und P ein Punkt auf einer der Seiten der Geraden gAB. Falls
∠PAB ≚ ∠PBA,
so folgt mit X24 sofort die behauptete Aussage. Angenommen also, dass etwa
∠PAB < ∠PBA
gilt. Sei BQ> eine im Inneren von ∠PBA verlaufende Halbgerade, so dass
∠PAB ≚ ∠QBA.
Dann existiert nach X18 genau
ein Punkt C zwischen A und P, in welchem BQ> die Strecke AP schneidet. Wegen
∠CAB ≚ ∠PAB ≚ ∠QBA ≚ ∠CBA
folgt mit X24 die Gleichschenkligkeit des Dreiecks ABC.
![]() X27
X27
Seien ABC und ABC’ zwei Dreiecke, wobei die Punkte C und C’ auf derselben Seite von AB liegen.
Wenn dann
AC ≡ AC’
und BC ≡ BC’
gilt, so ist C = C’.
[vgl. Euklid I.§7]
Beweis:
Mit dem Kongruenzsatzes sss
folgt unmittelbar ABC ≅ ABC’ und damit
∠CAB ≚ ∠C’AB.
Da C und C’ nach Voraussetzung auf derselben Seite von gAB liegen, gilt
AC> = AC’> wegen III.4. Zusammen mit
AC ≡ AC’
folgt wegen III.1 C = C’.
![]() X28
(Halbierung von Strecken)
X28
(Halbierung von Strecken)
Jede Strecke kann in zwei zueinander kongruente Teilstrecken zerlegt werden.
[vgl. Euklid I.§10]
Beweis:
Sei AB eine beliebige Strecke.
Die Punkte C und D seien so gewählt, dass C auf einer Seite von gAB und D
auf der anderen Seite von gAB liegt und die Kongruenzen
∠BAC ≚ ∠ABD
sowie
AC ≡ BD
gelten. Wegen X18 wird AB
von CD in genau einem Punkt geschnitten. Dieser Schnittpunkt soll
mit M bezeichnet werden.
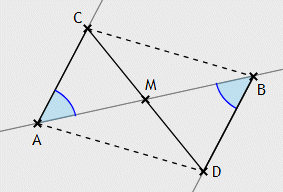
Mit dem Kongruenzsatz sws
folgt, dass die Dreiecke ABC und BAD zueinander kongruent sind, womit insbesondere
BC ≡ AD
gilt. Mit dem Kongruenzsatz sss
hat man dann DCA ≅ CDB, und somit
∠ACD ≚ ∠BDC,
also auch
∠ACM ≚ ∠BDM.
Mit dem Kongruenzsatz wsw
folgt schließlich AMC ≅ BMD und
damit AM ≡ MB.
Eine Strecke AB kann nach X28 halbiert, das heißt: in zwei zueinander kongruente Teilstrecken AM und MB zerlegt werden. Der Punkt M wird Mittelpunkt der Strecke AB genannt.
Sei ABC ein Dreieck. Dann heißen die Winkel ∠A, ∠B und ∠C die Innenwinkel des Dreiecks. Die Nebenwinkel der Innenwinkel nennt man die Außenwinkel des Dreiecks.

Ein Dreieck, in welchem einer der Innenwinkel ein rechter Winkel ist, heißt rechtwinklig.
![]() X29
(Satz vom Außenwinkel)
X29
(Satz vom Außenwinkel)
Jeder Außenwinkel eines Dreiecks ABC ist größer als jeder der beiden
nicht-anliegenden Innenwinkel.
[vgl. Euklid I.§16]
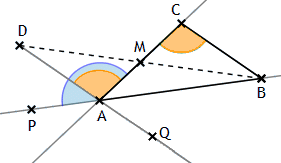

Beweis:
Sei M der Mittelpunkt von AC.
Der Punkt D auf der Halbgeraden BM> sei so gewählt, dass M zwischen D
und B liegt und BM ≡ MD
gilt. Dann folgt mit dem Kongruenzsatz sws
MBC ≅ MDA und damit
∠MCB ≚ ∠MAD.
Sei P ein Punkt auf BA> mit _PAB_ und Q ein Punkt auf DA> mit _DAQ_. Dann bleibt noch zu zeigen, dass ∠MAD < ∠MAP gilt: Mit dem Axiom von Pasch erkennt man, dass D und P auf derselben Seite von gAC liegen (denn gAC schneidet PQ und DQ) und dass D und C auf derselben Seite von gAB liegen (denn gAB schneidet CQ und DQ). Hieraus folgt, dass die Halbgerade AD> im Inneren von ∠MAP liegt, was zu zeigen war.
Ist M’ der Mittelpunkt von AB und D’ auf CM’> mit _CM’D’_ und CM’ ≡ M’D’, so folgt ∠CBM’ ≚ ∠D’AM’. Sei nun P’ ein Punkt auf CA> mit _PAC_ und Q’ ein Punkt auf D’A> mit _D’AQ_. Dann folgt auf ähnliche Weise wie oben, dass AD’> im Inneren von ∠M’AP’ liegt.
Damit ist die behauptete Aussage für die am Winkel ∠A anliegenden Außenwinkel bewiesen. Die Beweise für die anderen Außenwinkel verlaufen entsprechend.
Der Satz vom Außenwinkel (oft auch schwacher Außenwinkelsatz genannt) spielt beispielsweise in den Beweisen von X30, X31 und X34 eine entscheidende Rolle:
Gegeben sei eine Gerade g und ein Punkt P, der nicht auf g liegt. Dann gibt es nach X21 einen Punkt F auf g, so dass g und die Strecke PF einen rechten Winkel bilden.
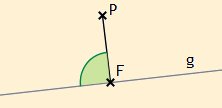
PF heißt Lotstrecke (oder kurz: Lot) von P auf g. Die Gerade gPF heißt Lotgerade (oder kurz: Lot) in F zu g. Man sagt üblicherweise: Eine Lotstrecke bzw. eine Lotgerade „ist senkrecht (oder orthogonal) zu g“. F wird Lotfußpunkt (oder kurz: Fußpunkt) genannt.
![]() X30
X30
Der Fußpunkt der Lotstrecke eines gegebenen Punktes P auf eine gegebene Gerade g ist eindeutig
bestimmt.
[vgl. Euklid I.§12]
Beweis:
Gegeben seien zwei voneinander verschiedene und auf einer Geraden g liegende Punkte F und F’. Ferner sei P
ein Punkt, der nicht auf g liegt. Dann ist PFF’ ein Dreieck. Die Annahme, dass sowohl PF als auch PF’ Lotstrecken von
P auf g sind, führt zu einem Widerspruch zu X29, denn aus diesem Satz folgt unmittelbar,
dass es in einem Dreieck nie zwei rechte Innenwinkel geben kann. Demzufolge müssen die Punkte F und F’ identisch sein.
![]() X31
X31
Es gibt in jedem Punkt einer Geraden genau ein Lot zu dieser
Geraden.
[vgl. Euklid I.§11]
Beweis:
Gegeben sei eine Gerade g. Seien ferner zwei voneinander verschiedene
Punkte F und A, die beide auf g liegen, beliebig gewählt. Sei dann B
derjenige Punkt auf <FA, so dass FA ≡ FB.
Dann gibt es nach X26 einen Punkt C
außerhalb von g, so dass das Dreieck ABC gleichschenklig ist. Mit dem
Kongruenzsatz sss folgt, dass die
Dreiecke FAC und FBC zueinander kongruent sind. Demnach sind ∠CFA
und ∠BFC zueinander kongruente Nebenwinkel,
also Rechte. gCF ist somit die (wegen I.1 eindeutig
bestimmte) Lotgerade in F zu g.
![]() X32
X32
In jedem Dreieck liegt der kleineren Seite der kleinere Winkel gegenüber.
[vgl. Euklid I.§18]
Gilt in einem Dreieck ABC beispielsweise AB < AC, so folgt ∠C < ∠B.
Beweis:
Sei in einem Dreieck ABC die Seite AB
kleiner als AC. Dann gibt es den Punkt D zwischen A und C mit
AD ≡ AB.
Das Dreieck BDA ist somit gleichschenklig und es folgt
∠DBA ≚ ∠ADB
wegen X23. Nach X29 ist
∠BCA < ∠ADB.
D liegt im Inneren von ∠CBA. Dies bedeutet, dass ∠DBA < ∠ABC. Insgesamt folgt also
∠BCA < ∠ADB < ∠ABC.
und damit die behauptete Aussage.
![]() X33
(Umkehrung von X32)
X33
(Umkehrung von X32)
In jedem Dreieck liegt dem kleineren Winkel die kleinere Seite gegenüber.
[vgl. Euklid I.§19]
Gilt in einem Dreieck ABC beispielsweise ∠C < ∠B, so folgt AB < AC.
Beweis:
Sei in einem Dreieck ABC der Winkel ∠C
kleiner als ∠B. Angenommen, es gelte dann
AB < AC nicht. Falls AB ≡ AC,
würde wegen X23
∠C ≚ ∠B folgen. Falls
AC < AB, wäre wegen X32
∠B < ∠C.
Beide Fälle führen demnach zum Widerspruch zu
∠C < ∠B,
was vorausgesetzt war.
![]() X34
X34
In jedem Dreieck ist die Summe zweier Seiten stets größer als die jeweilige dritte Seite.
[vgl. Euklid I.§20]
Beweis:
Es gibt den Punkt D auf AC> mit _ACD_ und CD ≡ BC.
Wegen der Gleichschenkligkeit des Dreiecks BDC ist
∠DBC ≚ ∠BDC.
Da C im Inneren von ∠DBA liegt,
gilt ∠DBC < ∠DBA.
Wegen der Kollinearität von A, C und D hat man
∠BDA < ∠DBA.
Mit X33 folgt
AB < AC + CD und hieraus die Behauptung.
![]() X35
(Kongruenzsatz „sww“)
X35
(Kongruenzsatz „sww“)
Wenn für zwei Dreiecke ABC und A’B’C’
∠A ≚ ∠A’, ∠B ≚ ∠B’ und AC ≡ A’C’
gilt, so sind beide Dreiecke zueinander kongruent.
[vgl. Euklid I.§26]
Beweis:
Sei ∠A ≚
∠A’, ∠B ≚
∠B’ und
AC ≡ A’C’.
Angenommen, es gilt
nicht AB ≡ A’B’.
Dann gibt es einen Punkt D’ auf A’B’> mit AB ≡ A’D’ und es folgt mit
sws, dass ABC ≅ A’D’C’. Also
gilt insbesondere
∠A’D’C’ ≚ ∠ABC.
Andererseits war aber
∠A’B’C’ ≚ ∠ABC
vorausgesetzt. Das bedeutet im Fall
AB < A’B’ für das Dreieck D’B’C’, dass der
Außenwinkel ∠A’D’C’ kongruent zum nicht-anliegenden Innenwinkel
∠A’B’C’ ist bzw. im Fall
A’B’ < AB für das Dreieck B’D’C’, dass der
Außenwinkel ∠A’B’C’ kongruent zum nicht-anliegenden Innenwinkel
∠A’D’C’ ist, beides ein Widerspruch zu X29!
Aus AB ≡ A’B’
folgt mit dem Kongruenzsatz sws die Behauptung.
![]() X36
(Halbierung von Winkeln)
X36
(Halbierung von Winkeln)
Jeder Winkel kann auf genau eine Weise halbiert werden.
[vgl. Euklid I.§9]
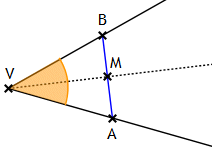
Beweis:
Gegeben sei ein beliebiger Winkel ∠(h,k) mit dem Scheitel
V. Man wähle die
Punkte A und B auf h bzw. auf k so, dass VA ≡ VB. Die Halbierung der Strecke AB
liefert nach X28 den eindeutig bestimmten Mittelpunkt M von AB.
Mit dem Kongruenzsatz sss folgt
VAM ≅ VBM und damit
∠AVM ≚ ∠MVB,
was zu beweisen war.
Unter Benutzung der Bezeichnungen aus X36 wird definiert: Die Halbgerade VM> heißt Winkelhalbierende des Winkels ∠AVB.
![]() X37
X37
In jedem Dreieck schneiden sich die drei Winkelhalbierenden in genau einem Punkt.
[vgl. Euklid IV.§4]

Beweis:
Gegeben sei ein beliebiges Dreieck ABC und zwei seiner Winkelhalbierenden, etwa wA, die den Winkel
∠BAC halbiert, und wB, die den Winkel
∠CBA halbiert. wA und wB schneiden sich wegen
X18
in einem Punkt W. Man zeigt mittels des Kongruenzsatzes sww und
unter Beachtung von III.3, dass die drei
Lotstrecken WD,
WE und WF zueinander kongruent sind. Deswegen ist EFW ein
gleichschenkliges Dreieck und wegen des Basiswinkelsatzes gilt
∠WFE ≚ ∠FEW.
Aus X20 zusammen mit X22 folgt ∠EFC ≚ ∠CEF,
was nach X24 bedeutet, dass
CF ≡ CE.
Hieraus folgt mit dem Kongruenzsatz
sws die Kongruenz WCF ≅ WCE.
Daraus ergibt sich
∠FCW ≚ ∠WCE
und hiermit die Behauptung.
Gegeben seien zwei voneinander verschiedene Geraden g und h, die von einer dritten Geraden l in zwei voneinander verschiedenen Punkten A und C geschnitten werden. B sei ein beliebig gewählter Punkt zwischen A und C. Wenn dann für einen Punkt P die Strecke PB weder von g noch von h geschnitten wird, so sagt man, dass P innerhalb von g und h liegt. Falls ein Punkt nicht innerhalb von g und h liegt, so liegt er außerhalb von g und h.
Werden zwei voneinander verschiedene Geraden g und h von einer dritten Geraden k in zwei voneinander verschiedenen Punkten geschnitten, so erhält man vier Paare von zueinander kongruenten Scheitelwinkeln. Sind von diesen insgesamt acht Winkeln je zwei Winkel keine Nebenwinkel und liegen die inneren Punkte des einen bzw. die inneren Punkte des anderen Winkels auf derselben Seite von k und liegen alle inneren Punkte von genau einem der beiden Winkel außerhalb von g und h, so sind beide Winkel Stufenwinkel.
Ersetzt man einen von zwei gegebenen Stufenwinkeln durch seinen Scheitelwinkel und behält den anderen Stufenwinkel bei, so erhält man zwei Wechselwinkel.
![]() X38
X38
Wenn zwei Geraden g und h von einer dritten Gerade derart geschnitten werden, dass Wechselwinkel
zueinander kongruent sind, so sind g und h parallel zueinander.
[vgl. Euklid I.§27]
Beweis:
Seien g und h zwei Geraden, die von einer dritten Geraden in voneinander verschiedenen Punkten A und B
geschnitten werden. Angenommen, g und h haben einen gemeinsamen Punkt C. Sei D irgendein Punkt auf CB> mit
_CBD_. Wegen der vorausgesetzten Kongruenz von Wechselwinkeln folgt dann, dass beispielsweise der Innenwinkel
∠A des Dreiecks ABC zum nicht-anliegenden Außenwinkel
∠ABD kongruent ist, im Widerspruch zum Satz vom Außenwinkel.
![]() X39
X39
Wenn zwei Geraden g und h von einer dritten Gerade l derart geschnitten werden, dass
Stufenwinkel zueinander kongruent sind, oder innerhalb von g und h und auf
derselben Seite von l liegende Winkel zusammen zwei Rechten entsprechen,
so sind g und h parallel zueinander.
[vgl. Euklid I.§28]
Beweis:
Der Satz folgt sofort aus X38 zusammen mit X17
und der Tatsache, dass sich Nebenwinkel immer zu zwei Rechten ergänzen.
![]() X40
X40
Sei g eine Gerade und P ein Punkt, der nicht auf g
liegt. Dann gibt es mindestens eine Gerade h durch P, so dass h parallel zu g ist.
[vgl. Euklid I.§31]
Beweis:
Sei die Gerade g beliebig gewählt, k eine zweite Gerade und P ein Punkt auf k. Falls
k||g, so ist nichts zu zeigen. Seien also g und k zwei Geraden, die sich in einem Punkt
S schneiden. Dann kann nach III.4 einer der von g und k eingeschlossenen Winkeln
an einer von P ausgehenden Halbgerade so abgetragen werden, dass sich zueinander kongruente Wechselwinkel ergeben.
Der Beweis von X40 ist der Nachweis dafür, dass eine Gerade, die durch einen gewissen Punkt läuft und parallel zu einer gegebenen Geraden ist, existiert. Das sogenannte Parallelenproblem, nämlich einen Weg zu finden, die Eindeutigkeit derartiger Parallelen auf der Grundlage der anderen Axiome der Geometrie herzuleiten, hat sich als unlösbar erwiesen. Das heißt: will man eindeutig existierende Parallelen haben, so muss man dies axiomatisch festlegen.
Dementsprechend hat Euklid in seinem fünften Postulat gefordert, „dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind.“
Die von Hilbert und bis heute üblicherweise verwendete Formulierung des zu Euklids Postulat äquivalenten Parallelenaxioms geht angeblich auf den schottischen Mathematiker John Playfair (1748−1819) zurück („Given a line and a point not on the line, there exists a unique line through the point parallel to the given line“) und lautet beispielsweise wie folgt:
Parallelenaxiom
![]() IV.
Ist g eine Gerade und P ein Punkt, der nicht auf g liegt, so gibt es genau eine
Parallele h zu g derart, dass P auf h liegt.
IV.
Ist g eine Gerade und P ein Punkt, der nicht auf g liegt, so gibt es genau eine
Parallele h zu g derart, dass P auf h liegt.
Wegen X40 würde es in IV ausreichend sein zu fordern, dass es höchstens eine Parallele h zu g gibt derart, dass P auf h liegt.
Die Annahme, dass es zu einer gegebenen Gerade mehrere Parallelen durch einen vorgegebenen Punkt geben kann, führt zur hyperbolischen nichteuklidischen Geometrie (zuerst entwickelt und veröffentlicht von den Mathematikern Nikolaj Ivanovič Lobačevskij und János Bolyai); die Annahme, dass es zu einer gegebenen Gerade und einem Punkt, der nicht auf der Geraden liegt, keine Parallele gibt, führt zur elliptischen Geometrie.
![]() X41
X41
Werden zwei zueinander parallele Geraden g und h von einer dritten Gerade l in zwei voneinander
verschiedenen Punkten geschnitten, so sind jeweilige Wechselwinkel bzw. Stufenwinkel zueinander kongruent und die innerhalb
von g und h auf derselben Seite von l entstehenden Winkel sind zwei Rechten gleich.
[vgl. Euklid I.§29]
Beweis:
Seien g und h zwei zueinander parallele Geraden und k eine Gerade, die g und h in zwei voneinander verschiedenen
Punkten S bzw. T schneidet. Sei ferner G ein von S verschiedener Punkt auf g, H ein von T verschiedener Punkt auf h derart,
dass G und H auf verschiedenen Seiten von k liegen.
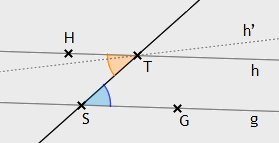
Sei nun angenommen, dass beispielsweise die Wechselwinkel ∠GST und ∠HTS nicht kongruent zueinander sind. Ohne Beschränkung der Allgemeinheit sei ∠GST < ∠HTS. Wird ein zu ∠GST kongruenter Winkel an der Halbgeraden TS> abgetragen, und zwar nach der Seite von k, auf der sich das Innere von ∠GST nicht befindet, so erhält man wegen X38 eine zweite Parallele h’ zu g durch T, im Widerspruch zum Parallelenaxiom.
Aus X41 zusammen mit dem Parallenaxiom folgt unter Beachtung von III.6 unmittelbar der nächste Satz:
![]() X42
X42
Sind zwei Geraden g und h zu einer dritten Geraden parallel, so sind auch g und h parallel
zueinander.
[vgl. Euklid I.§30]
![]() X43
X43
Gegeben sei ein Winkel ∠(g,h). Der von beliebigen Lotgeraden auf g bzw.
auf h gebildete Winkel ist kongruent zu ∠(g,h).
Beweis:
Gegeben seien die Winkel ∠(g,h)
mit dem Scheitel V sowie ∠(g’,h’) mit dem Scheitel V’, und zwar derart, dass g’ senkrecht
zu g bzw. h’ senkrecht zu h ist. Der Schnittpunkt von g und g’ sei mit G, derjenige von h und h’ mit H bezeichnet. Ohne
Beschränkung der Allgemeinheit sei die Situation so gewählt, dass V und H auf ein und derselben Seite von g’ liegen.
Die durch V’ gehende und zu g parallele Gerade sei mit g*, die ebenso durch V’ gehende und zu h parallele Gerade sei
mit h* bezeichnet. S sei der gemeinsame Punkt von g und h*, S* der gemeinsame Punkt von g* und h.
H* auf h* sei so gewählt, dass V’ zwischen H* und S liegt.
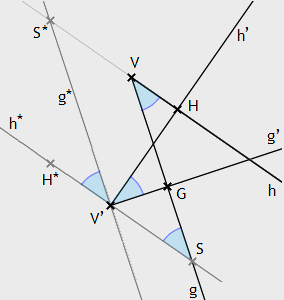
∠SVH und ∠VSV’ sind Wechselwinkel, ∠VSV’ und ∠S*V’H* Stufenwinkel. Demnach gilt ∠SVH ≚ ∠S*V’H*. Sowohl ∠HV’H* als auch ∠GV’S* sind rechte Winkel, also zueinander kongruent. Aus ∠HV’H* − ∠HV’S* = ∠S*V’H* und ∠GV’S* − ∠HV’S* = ∠GV’H folgt demzufolge ∠S*V’H* ≚ ∠GV’H und damit die Behauptung.
![]() X44
(Satz über die Winkelsumme im Dreieck)
X44
(Satz über die Winkelsumme im Dreieck)
In jedem Dreieck ist jeder Außenwinkel gleich der Summe der
nicht-anliegenden Innenwinkel. Die Summe der drei Innenwinkel entspricht stets zwei Rechten.
[vgl. Euklid I.§32]
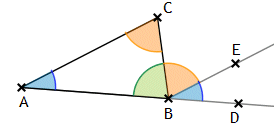
Beweis:
Gegeben sei ein beliebiges Dreieck ABC. D sei ein Punkt auf
gAB, so dass B zwischen A und D liegt. BE> sei eine zu gAC parallele Halbgerade, wobei
E auf derselben Seite von gAB liegen soll wie C. Dann
sind nach X41 sowohl die Stufenwinkel ∠BAC und
∠DBE als auch die Wechselwinkel ∠ACB und
∠EBC zueinander kongruent. Die Summe der zusammengefügten Winkel
∠DBE, ∠EBC und ∠CBA entspricht
zwei Rechten, womit die zweite behauptete Aussage bewiesen ist.
∠DBE + ∠EBC und ∠CBA
sind Nebenwinkel, woraus die erste behauptete Aussage folgt.
Sei M der Mittelpunkt einer beliebigen Strecke AB. Die Lotgerade in M zu gAB heißt Mittelsenkrechte von AB.
![]() X45
X45
Ein Punkt P liegt genau dann auf der Mittelsenkrechten einer Strecke
AB, wenn AP ≡ BP gilt.
Sei ABC ein Dreieck. Dann heißen die Mittelsenkrechten von AB, BC bzw. CA Mittelsenkrechten des Dreiecks ABC.
![]() X46
X46
Die drei Mittelsenkrechten eines Dreiecks ABC schneiden sich stets in einem Punkt
M. Es gilt
AM ≡ BM ≡ CM.
[vgl. Euklid IV.§5]

Beweis:
Gegeben sei ein beliebiges Dreieck ABC und die Mittelsenkrechte mc von
AB
sowie die Mittelsenkrechte mb von AC.
Es ist zunächst zu zeigen, dass sich mc und mb in
einem Punkt schneiden. Sei hierfür der Mittelpunkt von AC mit Mb bezeichnet.
Angenommen, mc und mb sind parallel zueinander. Dann sind zwei Fälle zu diskutieren: mb ist auch parallel zu gAB oder aber mb ist nicht parallel zu gAB. Der erste Fall liefert wegen X42 einen Widerspruch, denn mc schneidet gAB nach Voraussetzung. Im zweiten Fall schneiden sich mb und gAB, etwa im Punkt S. Dann hat aber das Dreieck ASMb wegen mc||mb zwei rechte Winkel im Widerspruch zu X44. Die Annahme mc||mb hat sich also als falsch herausgestellt, was zu zeigen war.
Wird der Schnittpunkt von mc und mb mit M bezeichnet, so gilt wegen X45 AM ≡ BM sowie AM ≡ CM, also auch BM ≡ CM. Dies bedeutet (wiederum wegen X45), dass M auf der Mittelsenkrechten von BC liegt. Hieraus folgt die behauptete Aussage.
Streckenlängen und Winkelweiten
![]()
In einer Hilbertebene kann man feststellen, ob eine gegebene Strecke kleiner oder größer als eine andere gegebene Strecke ist. Man kann zudem überprüfen, ob Strecken zueinander kongruent sind oder nicht. Es ist jedoch nicht möglich herauszufinden, wieviel mal eine gegebene Strecke größer oder kleiner ist als eine andere gegebene Strecke. Das Gleiche gilt in entsprechender Weise für Winkel. Mit anderen Worten: Auf der Grundlage der bisherigen Axiome ist es nicht möglich, Streckenlängen oder Winkelweiten zu messen.
Messen von Streckenlängen
Um Streckenlängen messen zu können, wird eine Abbildung ℓ benötigt, die in eindeutiger Weise jeder Strecke AB eine positive reelle Zahl μ zuordnet, wobei einer speziell gewählten Einheitsstrecke PQ die Zahl 1 zugeordnet wird. Die Maßzahl μ gibt dann die Länge von AB an, und zwar relativ zur Länge von PQ. Man wird von dieser Abbildung erwarten, dass zu kongruenten Strecken gleich große Maßzahlen gehören und dass die Maßzahl einer aus zwei Teilstrecken zusammengesetzten Strecke gleich der Summe der Maßzahlen dieser Teilstrecken ist. Demzufolge muss ℓ die folgenden drei Eigenschaften besitzen:
(S1) AB ≡ CD
⇒ ℓ(AB) = ℓ(CD)
(S2) ℓ(AB + BC)
= ℓ(AB) + ℓ(BC)
(S3) Es gibt eine Strecke PQ mit ℓ(PQ) = 1.
Eine Abbildung mit diesen drei Eigenschaften wird Längenfunktional genannt. Indem festgelegt wird, dass für eine bestimmte Strecke PQ ℓ(PQ) = 1 gelten soll, wird diese Strecke zum Eichmaß erklärt.
![]() X47
X47
Unter Voraussetzung des Archimedischen Axioms existiert für die Strecken einer Hilbertebene ein Längenfunktional. Mit der
Wahl eines Eichmaßes ist das Längenfunktional eindeutig bestimmt.
Archimedisches Axiom
![]() V.1
V.1
Sei AB eine beliebig gewählte Strecke auf einer Geraden g. Dann gibt es stets eine von 0 verschiedene natürliche Zahl n und
aufeinander folgende Punkte
A, C1, C2, ..., Cn
auf g, so dass Folgendes gilt:
(1) CiCi+1 ≡ AC1
für i = 1, 2, ..., n−1
(2) B liegt zwischen C0 und Cn, aber
nicht zwischen C0 und Cn−1.
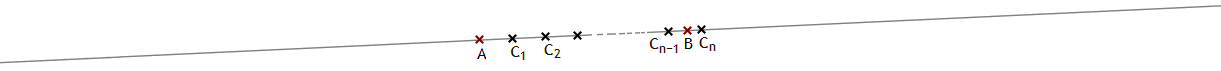
Das vermutlich auf Eudoxos von Knidos zurückgehende, aber nach Archimedes benannte Axiom (von Hilbert auch Axiom des Messens genannt) besagt, dass es weder „unendlich kleine“ noch „unendlich große“ Strecken geben kann, denn mit jeder noch so kleinen Strecke lässt sich, wenn man diese nur genügend oft aneinandersetzt, eine Strecke konstruieren, die größer ist als jede noch so große Strecke. Im Bereich der Zahlen gilt Entsprechendes: ℚ, die Menge aller rationalen Zahlen, und ℝ, die Menge der reellen Zahlen, sind archimedisch angeordnete Körper (vgl. insbesondere Q12 und Q14; siehe auch X82).
Beweis von X47:
Mit der Abbildung ℓ soll jeder Strecke eine positive reelle Zahl
zugeordnet werden, und zwar derart, dass ℓ die unter
(S1), (S2) und (S3) geforderten Eigenschaften besitzt.
(I)
Im Hinblick auf (S2) ist es zwingend, dass für jede beliebige Strecke ST
ℓ(SM1)
= 12·ℓ(ST)
und
ℓ(ST + ST) = ℓ(ST) + ℓ(ST)
festgelegt wird, wobei mit M1 der Mittelpunkt von ST bezeichnet wurde. Ist M2 der Mittelpunkt von SM1, M3 der Mittelpunkt von SM2, und so fort, so ergibt sich nach k-maliger Streckenhalbierung
(*) ℓ(SMk) = 12k·ℓ(ST).
Ist ST1 die Verlängerung von ST mit sich selbst, ST2 die Verlängerung von ST1 mit ST, und so weiter, so hat man nach k-maliger Streckenverlängerung
(**) ℓ(STk) = k·ℓ(ST).
Sei nun für eine Referenzstrecke PQ
ℓ(PQ) = 1
festgesetzt. Damit ist (S3) erfüllt.
(II)
Es soll nun gezeigt werden, dass ℓ additiv ist. Seien hierzu drei
kollineare Punkte A, B und C gegeben, wobei B zwischen A und C liegt. Man halbiere nun PQ
solange, bis ein genügend großes k gefunden wurde mit PMk < AB und
PMk < BC. Nach V.1
gibt es dann einerseits Punkte C1, C2, ..., Cn
auf der Halbgeraden BA> derart, dass
BC1 ≡ CiCi+1 ≡ PMk für alle i = 1, 2, ..., n−1
gilt und dass A zwischen B und Cn, aber nicht zwischen B und Cn−1 liegt. Andererseits gibt es Punkte D1, D2, ..., Dm auf der Halbgeraden BC> derart, dass
BD1 ≡ DiDi+1 ≡ PMk für alle i = 1, 2, ..., m−1
gilt und dass C zwischen B und Dm, aber nicht zwischen B und Dm−1 liegt. Dann folgt insbesondere mit (*) und (**) sowohl
n−12k ≤ ℓ(BA) < n2k
als auch
m−12k ≤ ℓ(BC) < m2k.
Hieraus ergibt sich (aus geometrischer Sicht)
m+n−22k ≤ ℓ(AC) < m+n2k
und rein arithmetisch (ℓ(BA) und ℓ(BC) sind positive reelle Zahlen!)
m+n−22k ≤ ℓ(BA) + ℓ(BC) < m+n2k.
Also hat man
|ℓ(BA) + ℓ(BC) − ℓ(AC)| < 12k−1.
Weil k in dieser Abschätzung beliebig groß werden darf, folgt
ℓ(AB) + ℓ(BC) = ℓ(AC).
Damit ist (S2) erfüllt.
(III)
Es bleibt noch nachzuweisen, dass die Maßzahl ℓ(AB) für eine beliebig gewählte Strecke AB in
eindeutiger Weise (relativ zu PQ) bestimmbar ist. Hierzu müssen drei Fälle unterschieden werden.
(i) AB ≡ PQ. Dann ist ℓ(AB) = 1. Fertig.
(ii) PQ < AB. Dann gibt es den Punkt C1 zwischen A und B mit AC1 ≡ PQ und es ist ℓ(AC1) = 1.
(iii) AB < PQ. Dann wird PQ schrittweise solange halbiert (PM1, PM2, PM3, ...), bis eine natürliche Zahl k gefunden wird, für die PMk < AB gilt. Dann gibt es den Punkt C1 zwischen A und B mit AC1 ≡ PMk und es ist wegen (*) ℓ(AC1) = 12k.
Nach Festlegung des Punktes C1 in den Fällen (ii) bzw. (iii) konstruiere man alle anderen Punkte Ci wie in V.1 beschrieben. Falls B = Cn−1 gilt, so ist nach (**) ℓ(AB) = (n−1)·ℓ(AC1). Andernfalls liegt B zwischen Cn−1 und Cn. In diesem Fall wird der Punkt Cn−1 zu D1 und Cn zu M0 umbenannt. Danach wird die Strecke D1M0 schrittweise halbiert (j = 1, 2, ...), und zwar nach folgendem Verfahren:
Ist nach dem j-ten Halbierungsschritt B < Mj, so setze man Dj+1 = Dj sowie zj = 0 und halbiere danach im (j+1)-ten Schritt die Strecke Dj+1Mj. Ist nach dem j-ten Halbierungsschritt Mj < B, so setze man Dj+1 = Mj sowie zj = 1 und halbiere danach im (j+1)-ten Schritt die Strecke Dj+1Mj−1. Ist nach dem j-ten Halbierungsschritt Mj = B, so setze man zj = 1 und breche ab.
Dies soll anhand eines Beispiels illustriert werden:

Dieses Halbierungsverfahren liefert eine gegen den Punkt B konvergente Punktfolge D1, D2, D3, ..., denn es gilt unter Beachtung von (II)
ℓ(Cn−1B) = ℓ(AC1)·∞∑j = 1zj2j.
Die Reihe ∞∑j = 1zj2j wird von
der konvergenten geometrischen Reihe ∞∑j = 112j
majorisiert. Der Wert von ℓ(Cn−1B) ist somit nach dem
Majorantenkriterium eindeutig bestimmt und die Maßzahl von AB gefunden:
ℓ(AB) = (n−1)·ℓ(AC1) + ℓ(Cn−1B).
Für eine zu AB kongruente Strecke A’B’ ergibt sich nach gleicher Konstruktion derselbe Wert. Kurz gesagt:
AB ≡ A’B’ ⇒ ℓ(AB) = ℓ(A’B’).
Damit ist die erste für ℓ geforderte Eigenschaft (S1) nachgewiesen.
(IV)
Seien ℓ und ℓ’ zwei Abbildungen, die (S1), (S2) und (S3) erfüllen.
Dann ergibt sich nach (I) bis (III) sofort, dass für alle Strecken AB
ℓ(AB) = ℓ’(AB)
gilt. Also ist ℓ = ℓ’ und demzufolge ℓ eindeutig bestimmt.
Sind A und B zwei Punkte, so wird mit
|AB| =def
|

|
0, falls A = B |
| ℓ(AB) sonst |
der Abstand zwischen A und B definiert.
Wegen X47 zusammen mit X34 hat man sofort den folgenden Satz:
![]() X48
(Dreiecksungleichung)
X48
(Dreiecksungleichung)
Sei ℓ das Längenfunktional für die Strecken einer Hilbertebene mit einem beliebig, aber fest gewählten Eichmaß. Dann
gilt für beliebige Punkte A, B und C
ℓ(AC) ≤ ℓ(AB) + ℓ(BC).
![]() X49
X49
Gegeben sei eine Gerade g und ein Punkt P, der nicht auf g
liegt. Dann ist PF genau dann das Lot von P auf g, wenn für alle von
F verschiedenen Punkte Q auf g
PF < PQ
gilt.
Beweis:
(i) Ist PF das Lot von P auf eine beliebig vorgegebene Gerade g und Q ein von F verschiedener, aber ansonsten beliebig
gewählter Punkt auf g, so ist der Winkel ∠QFP ein Rechter und damit wegen
X44 der größte Winkel im Dreieck FQP. Mit
X33 folgt PF < PQ.
(ii) Es gelte nun umgekehrt PF < PQ für einen Punkt F auf g und für alle von F verschiedenen Punkten Q auf g. Sei ferner PF* das Lot von P auf g. Die Annahme, dass F und F* voneinander verschiedene Punkte sind, führt nach (i) zu PF* < PF, und damit zu einem Widerspruch zur Voraussetzung.
Gegeben seien zwei zueinander parallele Geraden g und h. Sei ferner P ein beliebiger Punkt auf g und PF die Lotstrecke von P auf h. Dann nennt man ℓ(PF) den Abstand der Parallelen g und h.
![]() X50
X50
Gegeben seien die voneinander verschiedenen und zueinander parallelen Geraden g1, g2 und g3.
Werden diese drei Geraden von einer vierten Geraden g in den Punkten
A, B und C geschnitten, so sind die Abstände zwischen g1 und g2
bzw. zwischen g2 und
g3 genau dann einander gleich, wenn AB ≡ BC.

Mit anderen Worten: AB ≡ BC gilt unter den genannten Voraussetzungen genau dann, wenn g2 die Mittelparallele von g1 und g3 ist.
Messen von Winkelweiten
So wie mit der Abbildung ℓ jeder Strecke AB eindeutig eine Länge relativ zur Länge einer Einheitsstrecke zugeordnet werden kann, gibt es auch eine Abbildung b, die jedem Winkel in eindeutiger Weise eine Weite zuordnet, und zwar relativ zur Weite eines rechten Winkels. Hierzu wird festgelegt, dass für einen rechten Winkel ρ
b(ρ) = π2
gelten soll, wobei mit π die Kreiszahl gemeint ist.
![]() X51
X51
Sei b eine Abbildung, die jedem Winkel eine positive
reelle Zahl zuordnet, und zwar mit den folgenden Eigenschaften:
(W1) α ≚ β
⇒
b(α) = b(β)
(W2) σ
= α + β
⇒
b(σ)
= b(α) +
b(β)
(W3) Ist ρ ein rechter Winkel, so
gilt
b(ρ)
= π2.
Es gibt eine und nur eine solche Abbildung (vgl. X76 ).
Beweis:
Mit der Abbildung b soll jedem Winkel eine positive reelle Zahl
zugeordnet werden, und zwar derart, dass b die unter (W1), (W2) und (W3) geforderten
Eigenschaften besitzt.
(0)
Mit der Festsetzung
b(ρ) = π2
für einen rechten Winkel ρ ist (W3) erfüllt.
(I)
Nach X36 kann
jeder Winkel δ eindeutig halbiert werden.
Sei einer der beiden hierdurch entstehenden Winkel mit δ1
bezeichnet. Im Hinblick auf (W2) ist es zwingend, dass für jeden beliebigen Winkel δ
b(δ1)
= 12·b(δ)
und
b(δ + δ) =
b(δ) +
b(δ)
festgelegt wird. Ist δ2 einer der durch Halbierung von δ1, δ3 einer der durch Halbierung von δ2 entstehenden Winkel, und so fort, so ergibt sich nach k-maliger Winkelhalbierung
(*) b(δk) = 12k·b(δ).
Ist δI die Erweiterung von δ mit sich selbst, δII die Erweiterung von δI mit δ, und so weiter, so hat man nach K-maliger Winkelerweiterung
(**) b(δK) = K·b(δ),
wobei K nicht beliebig groß werden darf, weil δK stets kleiner als zwei Rechte bleiben muss.
(II)
Es soll nun gezeigt werden, dass b additiv ist. Seien hierzu zwei
miteinander verknüpfte Winkel ∠(h,k) und ∠(k,l) mit
gemeinsamem Scheitel V gegeben. Dann gibt es eine durch V gehende Gerade g derart, dass alle Punkte der
Halbgeraden h, k und l auf derselben Seite von g liegen. Man halbiere nun
den rechten Winkel ρ solange, bis ein
genügend großes j gefunden wurde, so dass b(ρj)
kleiner ist als jedem der durch h, k, l bzw. g eingeschlossenen Winkeln.
b(ρj)
wird an k beginnend fortgesetzt nach beiden Seiten abgetragen, und zwar solange, bis
h bzw. l sich im Inneren der beiden
jeweils letzten neu entstehenden Schenkel befinden.
Nach Beweisschritten, die denen im Beweis zu X47(II) entsprechen, folgt schließlich
b(∠(h,k)) + b(∠(k,l)) = b(∠(h,l))
und hieraus (W2).
(III)
Es bleibt noch nachzuweisen, dass die Maßzahl eines beliebig gewählten
Winkels in eindeutiger Weise (relativ zu ρ) bestimmbar ist.
Sei hierzu irgendein Winkel δ gegeben und
ein rechter Winkel dazu so gewählt, dass beide Winkel denselben Scheitel
besitzen, einen Schenkel gemeinsam haben und gemeinsame innere Punkte besitzen.
Dann müssen drei Fälle unterschieden werden:
(i) δ ≚ ρ. Dann ist b(δ) = π2. Fertig.
(ii) δ < ρ. Dann setze man δ1 = δ und z0 = 0.
(iii) ρ < δ. Dann wähle δ1 so, dass δ = ρ + δ1 und setze z0 = 1.
Unter Verwendung von (W2) folgt sowohl im Fall (ii) als auch im Fall (iii)
b(δ) = z0·π2 + b(δ1).
Nach Halbierung von ρ gibt es wiederum drei Möglichkeiten:
(i) δ1 ≚ ρ2. Dann ist b(δ1) = π4 und damit b(δ) = 34π. Fertig.
(ii) δ1 < ρ2. Dann setze man δ2 = δ1 und z1 = 0.
(iii) ρ2 < δ1. Dann wähle δ2 so, dass δ1 = ρ2 + δ2 und setze z1 = 1.
Nach diesem ersten Halbierungsschritt hat man im Fall (i)
b(δ) = z0·π2 + π4
bzw. im Fall (ii) oder (iii)
b(δ) = z0·π2 + z1·π4 + b(δ2).
Fortgesetztes Halbieren von ρ (ρ2, ρ4, ρ8, ...) liefert nach dem n-ten Schritt im Fall (i)
b(δ) = π2·n−1∑j = 0zj2j + π2n
bzw. im Fall (ii) oder (iii)
b(δ) = π2·n∑j = 0zj2j + b(δn+1).
In jedem Fall ist b(δ)
eindeutig bestimmt, denn die Reihe
∞∑j = 0zj2j
ist konvergent und die Folge b(δ),
b(δ1),
b(δ2),
... bricht entweder ab oder ist eine Nullfolge.
Für einen zum Winkel δ kongruenten Winkel δ’ ergibt sich nach gleicher Konstruktion derselbe Wert. Kurz gesagt:
δ ≚ δ’ ⇒ b(δ) = b(δ’).
Damit ist auch die erste für b geforderte Eigenschaft (W1) nachgewiesen.
(IV)
Seien b und b’ zwei Abbildungen, die (W1),
(W2) und (W3) erfüllen, so ergibt sich nach (I) bis (III) sofort, dass für alle Winkel
δ
b(δ) = b’(δ)
gilt. Also ist b = b’ und demzufolge b eindeutig bestimmt.
Vollständigkeit
Nach X47 wird mittels eines Längenfunktionals ℓ jeder Strecke eine Länge relativ zu einer bestimmten Referenzstrecke zugeordnet. Mit anderen Worten: Zu jeder Strecke gehört in eindeutiger Weise eine gewisse positive reelle Zahl. Man wird erwarten, dass auch die Umkehrung dieser Aussage wahr ist, nämlich dass es zu jeder positiven reellen Zahl r eine Strecke AB gibt mit ℓ(AB) = r. Aus den bisherigen Axiomen lässt sich dies jedoch nicht folgern. Dies führt zur Formulierung des letzten Hilbert’schen Axioms:
Ebenes Vollständigkeitsaxiom
![]() V.2
V.2
Die Elemente der ebenen Geometrie (Punkte, Geraden) bilden ein System von
Dingen, welches bei Aufrechterhaltung sämtlicher genannten Axiome keiner Erweiterung mehr fähig ist.
Hilbert bemerkt zu seinem Axiom der Vollständigkeit (Grundlagen der Geometrie, §8):
Die Aufrechterhaltung sämtlicher Axiome, von der in diesem Axiom die Rede ist, hat man so zu verstehen, daß nach der Erweiterung sämtliche früheren Axiome in der früheren Weise gültig bleiben sollen, d. h. sofern man die vorhandenen Beziehungen der Elemente, nämlich die vorhandene Anordnung und Kongruenz der Strecken und Winkel nirgends stört, also z. B. ein Punkt, der vor der Erweiterung zwischen zwei Punkten liegt, dies auch nach der Erweiterung tut, Strecken und Winkel, die vorher einander kongruent sind, dies auch nach der Erweiterung bleiben.
Nach V.2 ist es nicht möglich, etwa mit geschickt gewählten positiven reellen Zahlen neue Punkte auf einer gegebenen Gerade zu finden. Die Punkte auf einer Geraden liegen auf dieser nicht nur dicht, sondern darüberhinaus und von vornherein lückenlos. Aus diesem Grund lässt sich nun eine Zahlengerade definieren:
![]() X52
X52
Seien O und E zwei voneinander verschiedene Punkte auf einer Geraden g
mit O < E. Sei ferner ℓ
ein
Längenfunktional mit ℓ(OE) = 1
und E’ derjenige Punkt auf der zu OE> entgegengesetzten Halbgerade, für den
OE ≡ OE’ gilt. Dann ordnet die
Abbildung l, definiert durch
l(X) =def
|

|
0, falls X = O |
| ℓ(OX), falls X auf OE> | ||
| −ℓ(OX), falls X auf <OE |
jedem Punkt X auf g eineindeutig eine reelle Zahl zu.
Sei nun P ein beliebig gewählter Punkt, der nicht auf g liegt und F der nach X30 eindeutig bestimmte Fußpunkt von P auf g. Sei nun xp = l(F) und yp = +l(PF) oder = −l(PF) oder = 0, je nachdem, ob P auf der einen bzw. der anderen Seite von g oder auf g liegt. Dann kann man dem Punkt P das Zahlenpaar (xp; yp) eindeutig zuordnen. Umgekehrt folgt aus V.2, X31 und III.1, dass zu jedem Zahlenpaar (x; y) eindeutig ein Punkt gehört.
Mit der als x-Achse bezeichneten Geraden gOE und der als y-Achse bezeichneten Lotgeraden in O zu gOE ist ein nach René Decartes (1596−1650) benanntes kartesisches Koordinatensystem definiert (mit O(0; 0) als Koordinatenursprung) und man kann nach dem Vorhergehenden den folgenden Satz formulieren:
![]() X53
X53
Nach Wahl des Koordinatensystems gehört zu jedem Punkt P umkehrbar eindeutig ein Paar von rechtwinkligen
Koordinaten (xp; yp). Dabei erschöpfen die Punkte alle Paare reeller
Zahlen (x; y).
Seien gAB und gCD zwei voneinander verschiedene, durch die Punkte A und B bzw. durch C und D definierte Geraden. Dann heißt das Viereck ABCD genau dann ein Parallelogramm, wenn sowohl gAB||gCD als auch gAD||gBC gilt.
![]() X54
(Parallelogrammregel)
X54
(Parallelogrammregel)
Ist ABCD ein Parallelogramm, so gilt AB ≡ DC
und AD ≡ BC.
[vgl. Euklid I.§33]
![]() X55
X55
Gegeben sei ein Dreieck ZAB. Sei A1 der Mittelpunkt
von ZA und h die durch A1 gehende Parallele zu gAB. Dann ist der Schnittpunkt
von h und gZB der Mittelpunkt von ZB.
Beweis:
Nach dem Parallelenaxiom
gibt es genau eine durch A1 verlaufende Parallele zu gZB.
Nach dem Axiom von Pasch gibt es einen Schnittpunkt
dieser Parallelen mit AB. Dieser sei mit P und der aus dem
gleichen Grund existierende Schnittpunkt von h und gZB mit B1 bezeichnet.
Wegen X41 gilt ∠A1ZB1 ≚ ∠AA1P und ∠B1A1Z ≚ ∠BAZ. Mit dem Kongruenzsatz wsw folgt ZA1B1 ≅ A1AP und hiermit A1P ≡ ZB1. Andererseits folgt aus X54, dass A1P ≡ B1B. Mit III.2 folgt die behauptete Aussage.
![]() X56
X56
Seien ZA1> und ZB1> zwei Halbgeraden, die zusammen einen Winkel
definieren. Seien ferner A2, ..., An Punkte auf
ZA1> mit
Aj−1Aj ≡ ZA1 für j = 2, ..., n
und B2, ..., Bn Punkte auf ZB1> derart, dass alle jeweils durch Aj und Bj definierte Geraden gj parallel zueinander sind. Dann gilt
Bj−1Bj ≡ ZB1 für j = 2, ..., n.
Beweis:
Die durch A1 gehende und zu ZB1> parallele Gerade schneidet jede Gerade
gj. Die sich ergebenden Schnittpunkte seien mit Pj bezeichnet.
Der Satz wird nun mittels vollständiger Induktion
bewiesen:
Induktionsanfang:
Die behauptete Aussage gilt für n = 2
wegen X55.
Induktionsvoraussetzung:
Angenommen, der Satz ist bereits für ein gewisses m > 2 bewiesen.
Induktionssschluss:
Sei Aj−1Aj ≡ ZA1
sowie gi||gj
für i,j = 2, ..., m+1. Nach
Induktionsvoraussetzung gilt bereits
Bj−1Bj ≡ ZB1 für j = 2, ..., m.
Die Gerade durch die Punkte Bm−1 und Pm schneidet gm+1 in einem Punkt S. Wegen X50 gilt Bm−1Pm ≡ PmS. Die Anwendung von X55 auf das Dreieck Bm−1SBm+1 liefert Bm−1Bm ≡ BmBm+1, was zu beweisen war.
![]() X57
(Erster Strahlensatz und seine Umkehrung)
X57
(Erster Strahlensatz und seine Umkehrung)
Gegeben seien zwei Geraden gA1A2 und gB1B2,
die sich in einem Punkt Z schneiden, und zwar derart, dass
(i) A1
zwischen Z und A2 bzw. B1
zwischen Z und B2 liegt oder dass (ii)
Z
zwischen A1 und A2 bzw. zwischen B1
und B2 liegt. Wenn dann gA1B1 und gA2B2
parallel zueinander sind, so gilt
ℓ(ZA1)ℓ(ZA2) = ℓ(ZB1)ℓ(ZB2).
Ist umgekehrt diese Verhältnisgleichung erfüllt, so folgt die Parallelität von gA1B1 und gA2B2.
[vgl. Euklid VI.§2]
Die Verhältnisgleichung ℓ(ZA1)ℓ(ZA2) = ℓ(ZB1)ℓ(ZB2) ist äquivalent zu ℓ(ZA1)ℓ(ZB1) = ℓ(ZA2)ℓ(ZB2) = ℓ(A1A2)ℓ(B1B2).
Z heißt das Zentrum der jeweiligen Strahlensatzfigur.
Beweis von X57(i):
Gegeben seien zwei Geraden gA1A2 und gB1B2,
die sich in einem Punkt Z schneiden, und zwar derart, dass A1 zwischen
Z und A2 bzw. B1
zwischen Z und B2 liegt. Ferner seien gA1B1 und gA2B2
parallel zueinander.
Fall 1:
ℓ(ZA1)ℓ(ZA2)
ist eine rationale Zahl.
In diesem Fall gibt es zwei natürliche Zahlen n und m, so dass
ℓ(ZA1)ℓ(ZA2) = nn + m.
Man zerlege die Strecke ZA1 in n zueinander kongruente Teilstrecken Cj−1Cj (j = 1, ..., n) mit C0 = Z und Cn = A1. Dann kann unter Beachtung von (S2) die folgende Rechnung aufgemacht werden:
ℓ(A1A2)
= ℓ(ZA2) −
ℓ(ZA1)
= n+mn·ℓ(ZA1) − ℓ(ZA1)
= m·ℓ(ZA1)n
= m·ℓ(ZC1)
ℓ(A1A2) = m·ℓ(ZC1) besagt, dass auch A1A2 in gleicher Weise wie ZA1 zerlegt werden kann: in m zueinander kongruente Teilstrecken Cj−1Cj (j = n+1, ..., n+m) mit Cn+m = A2. Die durch die Punkte Cj gehenden und zu gA1B1 parallelen Geraden schneiden gB1B2, und zwar nach X56 in Punkten Dj mit
Dj−1Dj ≡ ZD1 für j = 2, ..., n+m,
wobei Dn = B1 und Dn+m = B2. Hieraus folgt
ℓ(ZB1)ℓ(ZB2) = n·ℓ(ZD1)(n + m)·ℓ(ZD1) = ℓ(ZA1)ℓ(ZA2).
Fall 2: ℓ(ZA1)ℓ(ZA2) ist eine irrationale Zahl.
Man wähle voneinander verschiedene Punkte C1, C2, ..., Cn+m auf gA1A2 mit
Cj−1Cj ≡ ZC1 für j = 2, ..., n+m,
und zwar derart, dass Cn = A1 ist und A2 zwischen Cn+m−1 und Cn+m liegt. Dann gilt
(n+m−1)·ℓ(ZC1) < ℓ(ZA2) < (n+m)·ℓ(ZC1)
und damit
(n+m−1)·ℓ(ZC1)n·ℓ(ZC1) < ℓ(ZA2)ℓ(ZA1) < (n+m)·ℓ(ZC1)n·ℓ(ZC1).
Die durch die Punkte Cj gehenden und zu gA1B1 parallelen Geraden schneiden gB1B2, und zwar in Punkten Dj so, dass
(n+m−1)·ℓ(ZD1)n·ℓ(ZD1) < ℓ(ZB2)ℓ(ZB1) < (n+m)·ℓ(ZD1)n·ℓ(ZD1)
gilt. Die letzten beiden Ungleichungen führen zu folgender Abschätzung:
|ℓ(ZA2)ℓ(ZA1) − ℓ(ZB2)ℓ(ZB1)| < 1n.
Hierbei kann n beliebig groß gewählt werden, also folgt
ℓ(ZA1)ℓ(ZA2) = ℓ(ZB1)ℓ(ZB2).
Gelte nun umgekehrt diese Verhältnisgleichung und sei P2 derjenige Punkt auf gB1B2 mit gA1B1||gA2P2, dann folgt mit dem Vorhergehenden
ℓ(ZA1)ℓ(ZA2) = ℓ(ZB1)ℓ(ZB2) = ℓ(ZB1)ℓ(ZP2).
Sowohl P2 als auch B2 liegen auf der Halbgeraden ZB1>, also gilt P2 = B2.
Teil (ii) des Satzes lässt sich auf gleiche Art beweisen.
Sind die rechtwinkligen Koordinaten zweier Punkte P und Q bekannt, so kennt man aufgrund des ersten Strahlensatzes auch die Koordinaten aller zwischen P und Q liegenden Punkte:
![]() X58
X58
Gegeben seien zwei
Punkte P(xp; yp) und Q(xq; yq).
Dann liegt der Punkt R(xr; yr) genau dann
zwischen P und Q, wenn es eine reelle Zahl t mit
0 < t < 1
gibt, so dass für die Koordinaten von R das Folgende gilt:
xr = xp +
t·(xq − xp)
yr = yp + t·(yq − yp).

![]() X59 (Zweiter Strahlensatz)
X59 (Zweiter Strahlensatz)
Gegeben seien zwei Geraden gA1A2 und gB1B2,
die sich in einem Punkt Z schneiden, und zwar derart, dass (i) A1
zwischen Z und A2 bzw. B1
zwischen Z und B2 liegt oder dass (ii)
Z
zwischen A1 und A2 bzw. zwischen B1
und B2 liegt. Wenn dann gA1B1 und
gA2B2 parallel zueinander sind, so gilt
ℓ(ZA2)ℓ(ZA1) = ℓ(A2B2)ℓ(A1B1).


Beweis:
Sei h die Gerade, die durch A1 geht und parallel zu
gB1B2 ist. Der Schnittpunkt von h und gA2B2 soll S heißen.

Die Anwendung des ersten Strahlensatzes auf diese Strahlensatzfigur mit A2 als Zentrum liefert (sowohl im Fall (i) wie abgebildet als auch im Fall (ii)) die Verhältnisgleichung
ℓ(A2Z)ℓ(A1Z) = ℓ(A2B2)ℓ(SB2).
Mit der Parallelogrammregel folgt ℓ(SB2) = ℓ(A1B1) und damit die Behauptung.
Die Umkehrung des zweiten Strahlensatzes ist nicht gültig!
Die Parallelogrammregel bzw. die Strahlensätze sind wesentliche Voraussetzung für die Beweise der folgenden Sätze X60, X61 und X62.
Gegeben sei ein Dreieck ABC. Die Lotstrecken von C auf gAB, von B auf gAC bzw. von A auf gBC heißen Höhen des Dreiecks ABC und sollen mit hc, hb bzw. ha bezeichnet werden. Die Lotgeraden in C zu gAB, in B zu gAC bzw. in A zu gBC heißen Höhengeraden des Dreiecks ABC.
![]() X60
X60
Die drei Höhen bzw. die Höhengeraden eines Dreiecks schneiden sich stets in einem Punkt.
Beweis:
Gegeben sei ein beliebiges Dreieck ABC mit den Höhen hc, hb
bzw. ha und deren Fußpunkten Fc, Fb bzw. Fa. Die Schnittpunkte der Parallelen
durch A zu BC, durch B zu CA und durch C zu AB bilden die Eckpunkte eines Dreiecks A’B’C’. Mit
der Parallelogrammregel hat man
BC ≡ CA ≡ A’B,
ebenso B’C ≡ CA’ und B’A ≡ AC’.
Somit sind die Geraden durch A und Fa, B und Fb sowie C und Fc die Mittelsenkrechten von
A’B’C’. Mit X46 folgt die Behauptung.

Gegeben sei ein Dreieck ABC. Die Mittelpunkte von AB, BC und CA seien mit Mc, Ma bzw. Mb bezeichnet. Die Strecken CMc, AMa und BMb heißen die Seitenhalbierenden von ABC und sollen mit sc, sb bzw. sa bezeichnet werden.
![]() X61
X61
Die drei Seitenhalbierenden eines Dreiecks schneiden sich stets in einem Punkt S.
S teilt sa, sb bzw. sc im Verhältnis 2 : 1.
Beweis:
Gegeben sei ein beliebiges Dreieck ABC mit den Seitenhalbierenden sb und sc,
die sich in einem Punkt S schneiden. Durch zweimalige Anwendung des ersten Strahlensatzes
(einmal mit A als Zentrum, das zweite Mal mit C als Zentrum) folgt, dass die Strecke AC durch sb und die zu
sb parallelen Geraden durch Mc bzw. Ma in vier
kongruente Teilstrecken zerlegt wird. Hieraus ergibt sich (wiederum mit
dem ersten Strahlensatz), dass ℓ(CS) = 2·ℓ(SMc)
gilt. Mittels sc und den zu sc parallelen Geraden durch Ma bzw. Mb folgt in
analoger Weise ℓ(BS) = 2·ℓ(SMb). Demnach gilt also
ℓ(CS)ℓ(SMc) = ℓ(BS)ℓ(SMb) = 2.

Die Seitenhalbierenden sa und sc schneiden sich in jedem Fall in einem Punkt S’. Mit entsprechender Argumentation wie oben folgt
ℓ(CS’)ℓ(S’Mc) = ℓ(AS’)ℓ(S’Ma) = 2.
Aus ℓ(CS’)ℓ(S’Mc) = ℓ(CS)ℓ(SMc) folgt unter Beachtung von III.1 S = S’ und damit die Behauptung.
![]() X62
X62
Gegeben sei ein Dreieck. Dann liegen der Schnittpunkt M der Mittelsenkrechten, der Schnittpunkt H der Höhengeraden und der
Schnittpunkt S der Seitenhalbierenden stets auf einer Geraden und es gilt
ℓ(HS) = 2·ℓ(SM).
Beweis:
In einem gleichseitigen Dreieck gilt S = M = H
und damit ist die behauptete Aussage trivialerweise erfüllt. Gegeben sei also ein Dreieck ABC mit verschieden langen Seiten. In
einem solchen Dreieck gibt es mindestens zwei Höhen, die nicht mit einer Seitenhalbierenden zusammenfallen. Ohne Beschränkung der
Allgemeinheit seien dies hc und hb.
Sei nun P derjenige Punkt mit der Eigenschaft, dass zum einen S zwischen P und M liegt und zum anderen ℓ(PS) = 2·ℓ(SM) gilt.
Mit X61 folgt ℓ(PS)ℓ(SM) = ℓ(CS)ℓ(SMc) und damit wegen X57(ii), dass die Geraden gCP und gMMc parallel zueinander sind. Auf die gleiche Weise folgt aus ℓ(PS)ℓ(SM) = ℓ(BS)ℓ(SMb) die Parallelität von gBP und gMMb. Demnach liegt P sowohl auf hc als auch auf hb, es gilt also P = H. Damit liegen H, S und M auf ein und derselben Geraden, wie zu zeigen war.
Die Gerade durch H, S und M wird Eulergerade genannt.
Die Maßzahl der bei einem Dreieck ABC dem Eckpunkt A gegenüberliegenden Seite BC soll in der Regel ab jetzt mit a, die Maßzahl der Seite AC mit b und die Maßzahl der Seite AB mit c bezeichnet werden.
Zwei Dreiecke ABC und A’B’C’ heißen zueinander ähnlich (in Zeichen: ABC ~ A’B’C’), wenn die entsprechenden Innenwinkel zueinander kongruent und die Seitenpaare BC und B’C’, CA und C’A’ sowie AB und A’B’ verhältnisgleich sind:
∠A ≚ ∠A’,
∠B ≚ ∠B’,
∠C ≚ ∠C’
a’a = b’b = c’c.
![]() X63
(Ähnlichkeitssätze)
X63
(Ähnlichkeitssätze)
Zwei Dreiecke ABC und A’B’C’ sind zueinander ähnlich, wenn
(i) je zwei sich entsprechende Winkel kongruent
(ii) alle drei Paare sich entsprechender Seiten verhältnisgleich
(iii) zwei Paare sich entsprechender Seiten verhältnisgleich und die jeweils von ihnen eingeschlossenen Winkel kongruent
sind.
Beweis:
Gegeben seien zwei Dreiecke ABC und A’B’C’.
(i) Es sei
∠A ≚ ∠A’,
∠B ≚ ∠B’,
∠C ≚ ∠C’.
Dann gibt es ein zu A’B’C’ kongruentes Dreieck A*B*C*, so dass CA> = CA*>
und CB> = CB*>. Es gilt ferner gAB||gA*B*
wegen X39. Mit dem ersten Strahlensatz
folgt ABC ~ A*B*C*
und damit auch ABC ~ A’B’C’.
(iii) Sei ohne Beschränkung der Allgemeinheit ∠C ≚ ∠C’ und a’a = b’b. Dann gibt es ein zu A’B’C’ kongruentes Dreieck A*B*C*, so dass CA> = CA*> und CB> = CB*>. Mit der Umkehrung des ersten Strahlensatzes schließt man auf die Parallelität von AB und A*B*, mit X39 folgt ∠A ≚ ∠A* sowie ∠B ≚ ∠B*, und mit (i) folgt schließlich ABC ~ A’B’C’.
(ii) Sei a’a = b’b = c’c vorausgesetzt und A* derjenige Punkt auf CA> mit CA* ≡ b’ und B* der Punkt auf CB> mit CB* ≡ a’. Wegen ℓ(CA*)b = ℓ(CB*)a ist dann nach der Umkehrung des ersten Strahlensatzes A*B* parallel zu AB. Mit dem zweiten Strahlensatz folgt ℓ(B*A*)c = b’b und damit A*B*C* ≅ A’B’C’. Wie bei (iii) folgt mittels X39 und (i) schließlich ABC ~ A’B’C’.
Ist in einem Dreieck ABC einer der Innenwinkel ein Rechter, so heißt dieses Dreieck rechtwinklig. Die dem rechten Winkel gegenüberliegende Seite heißt Hypotenuse, die anderen Seiten sind die Katheten.
Aus dem ersten Ähnlichkeitssatz X63(i) folgen in Verbindung mit dem Satz über die Winkelsumme im Dreieck drei wichtige Sätze:
![]() X64
(Satzgruppe des Pythagoras)
X64
(Satzgruppe des Pythagoras)
Gegeben sei ein rechtwinkliges Dreieck mit ∠C als rechtem Winkel. Die
Maßzahl der Höhe von C auf c soll mit h und die Maßzahlen der Hypotenusenabschnitte AF
und FB sollen mit q bzw. mit p bezeichnet werden.
Dann gilt der Höhensatz des Euklid:
h2 = p·q,
der Kathetensatz des Euklid:
a2 = c·p bzw. b2 = c·q,
und der Satz des Pythagoras:
c2 = a2 + b2.
[vgl. Euklid VI.§8]
Beweis:
Der Winkel ∠A wird an der Halbgeraden AB>
abgetragen, und zwar nach der Seite, auf welcher C nicht liegt. Auf der so entstehenden Halbgeraden gibt es den Punkt
C’ mit A’C’ ≡ AC.
Wegen des Kongruenzsatzes sws
folgt ABC ≅ ABC’.
Die Dreiecke FCA, FBC und C’BA sind ähnlich zueinander. Deswegen gelten die Verhältnisgleichungen
ph = hq, pa = ac und qb = bc.
Hieraus folgen unmittelbar die oben angegebenen Sätze.
![]() X65
X65
Gegeben seien zwei Punkte P(xp; yp) und Q(xq; yq)
mit ihren kartesischen Koordinaten. Dann gilt für die Maßzahl der Strecke PQ
ℓ(PQ) = √(xq − xp)2 + (yq − yp)2.
Beweis:
Die behauptete Formel folgt mit dem Satz des Pythagoras.
![]() X66
X66
Zwei Strecken AB und CD sind kongruent genau dann, wenn ℓ(AB) =
ℓ(CD).
Beweis:
Aufgrund der Eigenschaften des Längenfunktionals ℓ gilt
AB ≡ CD ⇒ ℓ(AB) = ℓ(CD)
bei vorgegebenem Eichmaß von vornherein. Es bleibt also nur noch die Umkehrung dieser Aussage zu zeigen. Gegeben seien hierzu zwei Strecken AB und CD mit ℓ(AB) = ℓ(CD) nach Wahl eines kartesischen Koordinatensystems mit OE> als x-Achse. Nach Axiom III.1 gibt es dann auf OE> einen eindeutig bestimmten Punkt S mit AB ≡ OS und daraus folgend auch mit ℓ(AB) = ℓ(OS). Aus demselben Grund gilt ebenso CD ≡ OT und ℓ(CD) = ℓ(OT) mit einem gewissen Punkt T auf OE>. Mit ℓ(OS) = ℓ(OT) folgt S = T und hieraus nach Axiom III.2 die Kongruenz von AB und CD.
Drei nicht-kollineare Punkte bestimmen stets einen Kreis: Sind A, B und C drei solche Punkte, so ist der Schnittpunkt M der Mittelsenkrechten des Dreiecks ABC der Kreismittelpunkt (kurz: Mittelpunkt) des mit A, B und C gegebenen Kreises; die Länge von MA, MB bzw. MC nennt man den Kreisradius r (kurz: Radius) dieses Kreises. Ein Punkt P liegt auf diesem Kreis genau dann, wenn ℓ(MP) = r.
Nach X46 ist sowohl der Mittelpunkt und demzufolge auch der Radius eines durch drei Punkte gegebenen Kreises stets eindeutig bestimmt. Jede Gerade, die durch den Mittelpunkt M eines gegebenen Kreises mit dem Radius r geht, hat mit diesem Kreis wegen X52 genau zwei Punkte gemeinsam: Es sind diejenigen Punkte D und E mit ℓ(MD) = r und ℓ(ME) = r.
![]() X67
X67
Sei mittels dreier Punkte A, B und C ein Kreis mit dem Mittelpunkt
M und dem Radius r gegeben. Gilt dann für einen Punkt M’
ℓ(M’P) = r für jeden auf diesem Kreis liegenden Punkt P, so folgt
M’ = M.
[vgl. Euklid III.§1]
Beweis:
Sei mittels dreier Punkte A, B und C ein Kreis mit dem Mittelpunkt M und dem Radius
r gegeben.
Angenommen, es gibt einen von M verschiedenen Punkt M’ derart, dass
ℓ(M’P) = r für jeden auf diesem Kreis liegenden Punkt P.
Dann gilt insbesondere ℓ(M’A) = r und
ℓ(M’B) = r, also M’A ≡ M’B.
Sei nun Mc der Mittelpunkt von AB und ferner D bzw. E diejenigen zwei Punkte auf der durch M und Mc gehenden Geraden gMMc mit ℓ(MD) = r und ℓ(ME) = r. Mit dem Kongruenzsatz sss ergibt sich AMcM’ ≅ BMcM’ und somit ∠M’McA ≚ ∠BMcM’. ∠M’McA und ∠BMcM’ sind demnach zueinander kongruente Nebenwinkel, also Rechte.
Demzufolge liegt neben D, M, Mc und E auch M’ auf der Geraden gMMc. Aus ℓ(M’D) = r und ℓ(MD) = r folgt dann M’ = M, was zu zeigen war.
![]() X68
X68
Ein Kreis und eine Gerade haben höchstens zwei Punkte gemeinsam.
Beweis:
Sei mittels dreier Punkte A, B und C ein Kreis mit dem Mittelpunkt M und dem Radius
r gegeben. Jede durch M
gehende Gerade hat mit diesem Kreis diejenigen zwei Punkte gemeinsam, deren
Abstand zu M gleich r ist.
Sei nun g eine Gerade, die mit dem gegebenem Kreis zwei Punkte S und T gemeinsam hat und nicht durch M geht. Ist H der Mittelpunkt von ST, so folgt aus HMS ≅ HMT, dass die Nebenwinkel ∠SHM und ∠MHT rechte Winkel sind.

Mit dem Satz des Pythagoras folgt, dass für jeden von S bzw. T verschiedenen Punkt P die Länge von PM entweder kleiner oder größer als r ist. Es folgt die Behauptung.
Hat eine Gerade mit einem Kreis genau zwei gemeinsame Punkte S und T, so nennt man ST im Fall dass M zwischen S und T liegt, einen Durchmesser, andernfalls eine Sehne.
![]() X69
X69
Ein Durchmesser schneidet eine Sehne in ihrem Mittelpunkt genau dann, wenn beide Strecken sich rechtwinklig
schneiden.
[vgl. Euklid III.§3]
Beweis:
Gegeben sei mittels dreier Punkte A, B und C ein Kreis mit dem Mittelpunkt M und ST eine beliebige Sehne,
die durch einen Durchmesser im Punkt H halbiert wird. Aus SH ≡ HT und
SM ≡ TM folgt mit dem Kongruenzsatz sss,
dass SHM ≅ THM und somit
∠MHS ≚ ∠THM.
∠MHS und ∠THM
sind demnach zueinander kongruente Nebenwinkel, also Rechte.
Sei nun umgekehrt vorausgesetzt, dass Durchmesser und Sehne sich rechtwinklig schneiden. Da das Dreieck STM gleichschenklig ist, folgt ∠HSM ≚ ∠THM wegen des Basiswinkelsatzes. Mit dem Kongruenzsatz sww folgt SHM ≅ THM und somit SH ≡ HT.
![]() X70
X70
Sei mittels dreier Punkte A, B und C ein Kreis mit dem Mittelpunkt M gegeben. Je drei auf diesem Kreis liegende,
aber ansonsten beliebig gewählte Punkte P, Q und R bestimmen genau den Kreis, auf dem sie liegen.
Beweis:
Gegeben sei mittels dreier Punkte A, B und C ein Kreis mit dem Mittelpunkt M und eine
beliebig gewählte Sehne ST. Sei ferner MF die (nach X31 eindeutig bestimmte)
Lotstrecke von M zu gST. Dann ist nach X69 die durch M und F gehende Gerade die Mittelsenkrechte eines
Dreiecks STP, wobei P ein von S und T verschiedener, aber ansonsten beliebig gewählter Punkt auf dem Kreis ist. Auf gleiche
Weise erhält man die zwei anderen, ebenso durch M gehenden Mittelsenkrechten des Dreiecks STP. Damit ergibt sich die
behauptete Aussage.
Gegeben sei ein Kreis mit zwei zueinander senkrechten Durchmessern AC und BD. Durch diese werden vier zueinander kongruente, gleichschenklige Dreiecke gebildet, deren Grundseiten demzufolge dieselbe Länge haben. Ferner folgt unter Verwendung von X23 und X44, dass alle Innenwinkel des Vierecks ABCD Rechte sind. Also ist ABCD ein Quadrat:
Ein Viereck, dessen Seiten gleichlang sind und aufeinander senkrecht stehen, nennt man ein Quadrat. Liegen die Eckpunkte des Quadrats auf einem Kreis, so sagt man: „Diesem Kreis ist das Quadrat einbeschrieben“.
![]() X71
X71
Zu einem Kreis gehören unendlich viele Punkte.
Beweis:
Gegeben sei ein beliebiger Kreis mit dem Mittelpunkt M und dem Radius
r, sowie ein diesem Kreis einbeschriebenes
Quadrat ABCD. Zu jedem der Winkel ∠AMB, ∠BMC,
∠CMD und ∠DMA existiert nach
X36 in eindeutiger Weise eine Winkelhalbierende. Auf jeder dieser
Winkelhalbierenden gibt es wegen III.1 einen Punkt, dessen Abstand zu M gleich
r ist
und der somit auf dem gegebenen Kreis liegt.
Dieser Prozess der Winkelhalbierung lässt sich beliebig oft fortsetzen, womit die Punkte auf dem Kreis − wenn man zudem
noch das Vollständigkeitsaxiom beachtet − lückenlos liegen.
Die Gesamtheit aller Punkte auf einem Kreis bildet die Kreislinie dieses Kreises.
Hat eine Gerade g mit einem Kreis genau einen Punkt T gemeinsam, so nennt man g eine Tangente an diesem Kreis. T heißt Berührpunkt.
Eine Tangente an einem Kreis hat stets die Eigenschaft, dass alle Punkte der Kreislinie außer dem Berührpunkt T auf ein und derselben Seite der Tangente liegen, denn es gibt ja nach Definition neben T keine weiteren Schnittpunkte von Kreislinie und Tangente. Jede von der Tangente verschiedene Gerade h, die durch deren Berührpunkt geht, hat dagegen die Eigenschaft, dass Punkte der Kreislinie auf beiden Seiten von h zu finden sind: h muss stets die Kreislinie in einem weiteren Punkt schneiden.
![]() X72
X72
Gegeben sei ein Kreis mit dem Mittelpunkt M und eine Tangente, die diesen Kreis im Punkt T berührt.
Dann ist MT die Lotstrecke von M auf die Tangente.
[vgl. Euklid III.§18]
Beweis:
Gegeben sei ein Kreis mit dem Mittelpunkt M und eine Tangente, die diesen Kreis im Punkt T
berührt. Angenommen, MT sei nicht die Lotstrecke von M auf die
Tangente. Dann gibt es auf der Tangente nach X31 einen
von T verschiedenen Punkt P derart, dass MP die Lotstrecke von M auf die
Tangente ist. Demzufolge ist der Winkel ∠TPM ein
Rechter und somit ∠MTP ein spitzer
Winkel. Mit X32 folgt MP < MT.
Da die Tangente außer T keinen weiteren Punkt mit dem Kreis gemeinsam hat, wird PM von der Kreislinie in einem Punkt S zwischen M und P geschnitten. Wegen MT = MS hat man mit MP < MT auch MP < MS im Widerspruch zu MS < MP. Die getroffene Annahme hat sich also als falsch erwiesen, was zu zeigen war.
![]() X73
X73
Gegeben sei ein Kreis und eine Tangente, die diesen Kreis im Punkt T
berührt. Dann geht die Lotgerade in T zur Tangente durch den Kreismittelpunkt.
[vgl. Euklid III.§19]
Beweis:
Gegeben sei ein Kreis mit dem Mittelpunkt M und eine Tangente, die diesen Kreis im Punkt T berührt. Sei ferner
g die Lotgerade in T auf die Tangente. Der zweite Punkt, den Kreis und Lotgerade gemeinsam haben, sei mit S bezeichnet.
Sei nun angenommen, dass M nicht auf g liegt. Von den Punkten auf der Tangente, die mit M zusammen auf ein und derselben Seite von g liegen, sei einer mit P bezeichnet. Dann ist sowohl ∠PTS als auch (nach X72) ∠PTM ein Rechter. Das ist aber nach X22 unmöglich, denn gemäß der getroffenen Annahme gilt ∠PTM < ∠PTS. Es folgt die behauptete Aussage.
Sind die Seiten eines einfachen Polygons gleich lang und zudem alle seine Innenwinkel gleich weit, so nennt man es ein regelmäßiges Polygon (oder: reguläres Polygon). Die Summe der Längen aller Seiten eines einfachen Polygons nennt man den Umfang dieses Polygons.
Gegeben sei ein Kreis K. Liegen alle Ecken eines einfachen Polygons auf K, so sagt man: „Diesem Kreis K ist das Polygon einbeschrieben“; hat jede Seite eines einfachen Polynoms genau einen Punkt mit K gemeinsam, so sagt man: „Diesem Kreis K ist das Polygon umbeschrieben“.
![]() X74
X74
Die Kreislinie eines Kreises lässt sich beliebig gut durch ein regelmäßiges Polygon approximieren.
Beweis:
Gegeben sei ein Kreis mit dem Mittelpunkt M und dem Radius
r. Diesem Kreis sei ein Quadrat einbeschrieben (das erste Glied
einer Folge (P2n)n=2..∞
von einbeschriebenen regulären Polygonen) und ein zweites Quadrat umbeschrieben
(das erste Glied einer Folge (Q2n)n=2..∞ von umbeschriebenen
regulären Polygonen), und zwar so, dass einander entsprechende
Quadratseiten parallel zueinander sind. Die Eckpunkte des Polynoms P2n
zusammen mit den Punkten, in denen die Mittelsenkrechten der Seiten von P2n den Kreis schneidet, bilden
die Eckpunkte von P2n+1. Die sich entsprechenden Seiten von P2n
und Q2n sind stets parallel zueinander. (Im obigen Diagramm sind die jeweils ersten beiden
Glieder beider Polygonfolgen dargestellt.) Das erste einbeschriebene Polygon hat vier, das zweite acht, das dritte
sechzehn Ecken, und so fort. Für die umbeschriebenen Polygone gilt Entsprechendes.
Wird die Länge einer Seite von P2n mit s2n und diejenige von Q2n mit t2n bezeichnet, dann kann mit Hilfe von X32 gezeigt werden, dass für alle n ≥ 2
s2n < 2·s2n+1 und 2·t2n+1 < t2n
gilt. Das aber bedeutet für die Umfänge U2n von P2n bzw. V2n von Q2n, dass für alle n ≥ 2
U2n < U2n+1 und V2n+1 < V2n
ist. Da zudem nach Konstruktion der Polynome der Umfang von P2n stets kleiner als derjenige von Q2n ist, bilden die Zahlenfolgen (U2n)n=2..∞ und (V2n)n=2..∞ eine Intervallschachtelung und diese hat nach Q26 genau einen inneren Punkt.
Mit anderen Worten:
lim n→∞U2n =lim n→∞V2n = U.
Der im Beweis von X74 ermittelte Grenzwert U nennt man den Umfang des Kreises.
![]() X75
X75
Der Kreisumfang U ist der Länge d eines Durchmessers proportional. Das heißt: Für jeden Kreis ist das
Verhältnis von U zu d stets eine Konstante.
Üblicherweise wird zwischen einem Durchmesser, der nach Definition eine Strecke ist, und seiner Länge sprachlich nicht unterschieden. Wenn aber von „dem Durchmesser eines Kreises“ die Rede ist, so ist immer die Länge eines der unendlich vielen Durchmesser dieses Kreises gemeint.
Beweis von X75:
Gegeben seien zwei Kreise mit dem gemeinsamen Mittelpunkt M, aber verschieden großen Radien:
r
< r’. Jeder der beiden Kreise kann nach
X74 durch ein reguläres Polygon mit
jeweils 2n Ecken approximiert werden, und zwar so, dass je zwei sich entsprechende Eckpunkte beider Kreise auf
einer der von M ausgehenden Halbgeraden liegen. Sich entsprechende Seiten, etwa AB und A’B’ mit den
Längen s2n bzw. s2n’, sind dann nach der Umkehrung
des ersten Strahlensatzes parallel zueinander.
Nach dem zweiten Strahlensatz gilt s2nr = s2n’r’, und zwar unabhängig von der Anzahl der Ecken beider Polynome. Daraus folgt für alle n ≥ 2
2n·s2nr = 2n·s2n’r’.
Ist U der Umfang des kleineren und U’ derjenige des größeren Kreises, so folgt
wegenlim n→∞2n·s2n = U
bzw.lim n→∞2n·s2n’ = U’ die
Behauptung.
Die Proportionalitätskonstante (oder: Proportionalitätsfaktor) zwischen dem Kreisumfang U und dem Kreisdurchmesser d ist die Kreiszahl π:
U = π·d.
Gegeben sei ein Kreis mit dem Mittelpunkt M und ein Winkel ∠AMB derart, dass die Punkte A und B auf dem gegebenen Kreis liegen. Dann nennt man ∠AMB einen Mittelpunktswinkel und den von A und B begrenzten Teil der Kreislinie den zu ∠AMB gehörenden Kreisbogen.
Ist der Umfang U eines Kreises bekannt, lässt sich die Länge eines Kreisbogens im Verhältnis zu U angeben. Hat ein Kreis den Radius 1 und ist ein gegebener Mittelpunktswinkel ein Rechter, so ist die Länge des zugehörigen Kreisbogens gleich π2.
In dieser Weise gehört zu jedem Winkel als Mittelpunktswinkel eines Kreises mit dem Radius 1 eindeutig ein Kreisbogen und damit auch die Länge dieses Kreisbogens. Die Länge des zur Summe zweier zusammengefügter Winkel gehörenden Kreisbogens ist offensichtlich gleich der Summe der Längen der zu den einzelnen Winkeln gehörenden Kreisbögen. Ferner sind die Längen der zu zwei zueinander kongruenten Winkeln gehörenden Kreisbögen stets einander gleich. Dies alles bedeutet:
![]() X76
X76
Gegeben sei ein beliebiger Winkel φ mit dem
Scheitel S sowie der Kreis mit S als Mittelpunkt und dem Radius 1.
Seien ferner A und B Punkte auf diesem Kreis mit
φ = ∠ASB
und x die Länge des von A und B begrenzten Kreisbogens. Dann ist die nach
X51 eindeutig existierende Abbildung b diejenige, die jedem
Winkel φ die reelle Zahl x zuordnet.
x ist das so genannte Bogenmaß des Winkels φ.
Ist F der Fußpunkt der Lotstrecke von B auf gSA, so gilt nach L16
ℓ(SF) = cos(x).
wobei statt „cos(x)“ üblicherweise auch „cos(φ)“ geschrieben wird: cos(x) = cos(φ).
Ist ein rechtwinkliges Dreieck ABC mit dem rechten Winkel β = ∠B gegeben, so folgt mit dem ersten Strahlensatz, dass
cos(α) = ℓ(AB)ℓ(AC) = cb
bzw.
cos(γ) = ℓ(CB)ℓ(AC) = ab
gilt. Das heißt: In jedem rechtwinkligen Dreieck ist der Kosinus jedes spitzen Innenwinkels stets gleich dem Verhältnis der Länge der diesem Winkel anliegenden Kathete (Ankathete) zur Länge der Hypotenuse.
![]() X77
(Kosinussatz)
X77
(Kosinussatz)
In jedem Dreieck ABC gelten die Identitätsgleichungen
a2 =
b2 + c2 − 2·b·c·cos(α),
b2 = a2 + c2 − 2·a·c·cos(β),
c2 = a2 + b2 − 2·a·b·cos(γ).
Beweis:
Es genügt, für ein beliebig gegebenes Dreieck ABC eine dieser drei Formeln zu beweisen, etwa die erste.
Fall 1: α ist kleiner als ein Rechter.
Sei CF die Höhe hc mit ℓ(hc) = h.
Der Fußpunkt F teilt die Strecke AB in zwei Teilstrecken mit den Längen q
bzw. p. Es gilt also c = p + q.
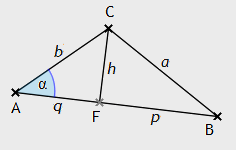
Wegen
h2 = b2 − q2
und
p2 = (c − q)2 = c2 − 2cq + q2
folgt aus a2 = h2 + p2
a2 = b2 + c2 − 2cq.
Mit q = b·cos(α) hat man die behauptete Identitätsgleichung.
Fall 2: α ist ein rechter Winkel.
In diesem Fall ist cos(α) =
0 und es gilt a2 = b2 + c2
nach dem Satz des Pythagoras.
Fall 3: α ist größer als ein Rechter.
Sei
wie oben CF die Höhe hc mit ℓ(hc) = h.
Der Fußpunkt F liegt außerhalb der Strecke AB und es gilt ℓ(FB) = q + c,
wenn die Länge der Strecke FA mit q bezeichnet wird.
Wegen
h2 = b2 − q2
folgt aus a2 = h2 + (q + c)2
a2 = b2 + c2 + 2cq.
Für den Winkel α’ gilt cos(α’) = qb. Da α und α’ Nebenwinkel sind, folgt mit L12
cos(α) = − qb
und hiernach
a2 = b2 + c2 − 2·b·c·cos(α).
![]() X78
X78
Gegeben seien drei beliebig gewählte nicht-kollineare
Punkte A(xa; ya), B(xb; yb)
und C(xc; yc) unter Verwendung eines kartesischen
Koordinatensystems. Sei ferner α der von AB und AC
eingeschlossene Winkel und (wie üblich) a = ℓ(BC),
b = ℓ(AC) und c = ℓ(AB). Dann gilt
b·c·cos(α) = (xb−xa)·(xc−xa) + (yb−ya)·(yc−ya).
Beweis:
Nach X77 ist
(*) b·c·cos(α) = 12·(b2 + c2 − a2).
Nach X65 gilt
b2 = (xc−xa)2 + (yc−ya)2,
c2 = (xb−xa)2 + (yb−ya)2 und
a2 = (xb−xc)2 + (yb−yc)2.
Ersetzt man in Gleichung (*) b2, c2 bzw. a2 durch die jeweiligen Summenterme, so ergibt sich anschließend nach längerer, aber elementarer Rechnung das gewünschte Ergebnis.
Gegeben sei ein beliebiger Winkel α = ∠BAC. Die Länge des nach X76 zu α gehörenden Kreisbogens sei x. Sei ferner
⟨AB,AC⟩ =def (xb−xa)·(xc−xa) + (yb−ya)·(yc−ya)
unter Verwendung der Bezeichnungen aus X78. Dann gilt für das Bogenmaß von α:
x = arccos ⟨AB,AC⟩ℓ(AB)·ℓ(AC).
arccos ist die Bezeichnung für die Umkehrfunktion der Kosinusfunktion cos, wobei hier der Definitionsbereich von cos auf das offene Intervall (0, π) eingeschränkt werden muss.
Gemäß X53 gehört nach Wahl eines Koordinatensystems zu jedem Punkt P umkehrbar eindeutig ein Paar von rechtwinkligen Koordinaten (xp; yp), wobei die Punkte alle Paare reeller Zahlen (x; y) erschöpfen.

In dieser Sichtweise wird das Tupel (xp; yp) als Eigenschaft des Punktes P verstanden. Die Idee, die Tupel (x; y) als Elemente des kartesischen Produktes ℝxℝ selbst als Punkte zu begreifen, führt zum Begriff der kartesischen Ebene.
Für die Definition der Winkelkongruenz bzw. der Streckenkongruenz in der kartesischen Ebene wird das Standard-Skalarprodukt
⟨(x; y),(x’; y’)⟩ = x·x’ + y·y’
bzw. die euklidische Norm
|(x; y)| = √x2 + y2
verwendet. Die üblichen Rechenoperationen in ℝxℝ ermöglichen die Addition bzw. die Subtraktion von Punkten der kartesischen Ebene:
(x; y) + (x’; y’) = (x + x’; y + y’)
(x; y) − (x’; y’) = (x − x’; y − y’).
(K1) Die Punkte der kartesischen Ebene sind die Elemente der Menge ℝxℝ.
(K2) Die Geraden der kartesischen Ebene sind Teilmengen von ℝxℝ, und zwar von der Form
g(a,b,c) =
{ (x; y) ∈∈ ℝxℝ |
ax+by+c = 0 },
wobei a, b und c beliebige reelle Zahlen sind mit der Einschränkung, dass
(a; b) ǂ (0; 0).
Ein Punkt (x; y) „liegt auf der Geraden g(a,b,c)“ (oder „gehört zu g(a,b,c)“) genau dann, wenn (x; y) ∈∈ g(a,b,c).
![]() X79
X79
Die kartesische Ebene erfüllt die Inzidenzaxiome
I.1 bis I.3.
Beweis:
Gegeben sei eine Gerade g(a,b,c) und zwei Punkte (x1; y1),(x2; y2) ∈∈ g(a,b,c).
Dann gilt

|
ax1 + by1 + c = 0 |
ax2 + by2 + c = 0. |
(1)
Mit der unter (K2) gemachten Voraussetzung, dass a und b nie
gleichzeitig den Wert 0 annehmen, wird dieses Gleichungssystem durch

|
a = y2 − y1 |
b = x1 − x2 |
|
c = x2y1 − x1y2 |
gelöst. Das heißt, die Koeffizienten a, b und c werden vollständig durch die Punkte (x1; y1) und (x2; y2) bestimmt, was der Forderung des Axioms I.1 entspricht.
(2)
Für Geraden g(a,0,c) ist im Hinblick auf I.2 nichts zu
zeigen. Sei also im Folgenden angenommen, dass x1 und x2
voneinander verschieden sind. Die die Gerade g(a,b,c) beschreibende Gleichung
(*) (y2 − y1)x + (x1 − x2)y
= x1y2 − x2y1
ist für x1 ǂ x2 äquivalent zu
(**) y = mx − mx1 + y1
mit
m = y2 − y1x2 − x1.
Seien nun (xP; yP) und (xQ; yQ)
zwei beliebig gewählte und voneinander verschiedene Punkte der vorgegebenen Geraden g(a,b,c). Dann gilt
wegen (**)

|
yP = mxP − mx1 + y1 |
yQ = mxQ − mx1 + y1. |
Die Anwendung von (*) auf (xP; yP) und (xQ; yQ)
liefert
m(xQ − xP)x + (xP − xQ)y
= xPyQ − xQyP.
Wird diese Gleichung mit x2 − x1xQ − xP
multipliziert, so erhält man anschließend nach längerer Rechnung schließlich die Gleichung
(*), entsprechend der Forderung des Axioms I.2.
(3)
Beispielsweise hat man mit (0; 0), (0; 1) und (1; 0) drei
Punkte, die nicht auf einer Geraden liegen.
Wegen X79 gilt auch in der kartesischen Ebene, dass zwei voneinander verschiedene Geraden entweder genau einen oder keinen gemeinsamen Punkt haben (vgl. X1). Zwei sich nicht schneidende Geraden sind parallel zueinander.
![]() X80
X80
Die kartesische Ebene erfüllt das Parallelenaxiom.
Beweis:
Gegeben sei eine Gerade g(a,0,c) und ein Punkt (xP; yP)
mit (xP; yP) ∉∉ g(a,0,c).
Die Gerade g(1,0,−xP) geht offensichtlich durch den Punkt (xP; yP),
ist parallel zu g(a,0,c) und ist die einzige Gerade mit diesen Eigenschaften.
Sei nun g(a,b,c) mit b ǂ 0 eine ansonsten beliebig vorgegebene Gerade, (xG; yG) ein Punkt mit (xG; yG) ∈∈ g(a,b,c) und (xP; yP) ein Punkt mit (xP; yP) ∉∉ g(a,b,c). Sei ferner g*(a*,b*,c*) mit b* ǂ 0 eine Gerade derart, dass (xP; yP) ∈∈ g*(a*,b*,c*). Dann gibt es eine reelle Zahl m, so dass alle Punkte (x; y) der Geraden g(a,b,c) der Gleichung
y = m(x − xG) + yG,
sowie eine reelle Zahl m*, so dass alle Punkte (x; y) der Geraden g*(a*,b*,c*) der Gleichung
y = m*(x − xP) + yP
genügen. Angenommen, g*(a*,b*,c*) schneidet g(a,b,c) immer, und zwar jeweils in einem gewissen, eindeutig bestimmten Punkt (xS; yS). Dann gilt
m(xS − xG) + yG = m*(xS − xP) + yP
und es folgt
xS(m − m*) = K
mit einer von xG, xP, yP, m und m*
abhängigen Zahl K. In dem einen einzigen Fall, wo m = m* gilt,
erhält man einen Widerspruch zur Annahme. In diesem Fall schneiden sich die Geraden g*(a*,b*,c*) und g(a,b,c) nicht und sind damit
parallel zueinander.
![]() X81
X81
Die kartesische Ebene erfüllt das Vollständigkeitsaxiom
V.2.
Beweis:
Die Menge der reellen Zahlen ist vollständig, anschaulich formuliert: In ℝ
gibt es keine Lücken.
Demzufolge ist auch ℝxℝ
vollständig.
Gegeben seien zwei voneinander verschiedene Punkte (xP; yP) und (xQ; yQ). Sei t eine beliebige reelle Zahl. Wenn dann für einen Punkt (xR; yR)
 |
xR = xP + t·(xQ − xP) |
| yR = yP + t·(yQ − yP) |
gilt, so gehören diese drei Punkte zu ein und derselben Geraden, denn unter der
Voraussetzung, dass sowohl axP + byP + c = 0 als auch
axQ + byQ + c = 0
gilt, folgt nach kurzer Rechnung, dass auch axR + byR + c = 0
gilt. Aus diesem Grund lässt sich jede Gerade parametrisieren: Zu
jedem Punkt auf einer durch zwei Punkte definierten Geraden gehört ein
bestimmter Wert von t. Umgekehrt ist wegen X81 jedem Wert von t eindeutig ein Punkt
auf dieser Geraden zugeordnet. Der Parameter t bezieht sich natürlich
stets auf die jeweilig vorgegebenen Punkte (xP; yP) und (xQ; yQ).
(K3) (xR; yR) liegt zwischen zwei voneinander verschiedenen Punkten (xP; yP) und (xQ; yQ) genau dann, wenn es eine reelle Zahl t mit 0 < t < 1 gibt, so dass
 |
xR = xP + t·(xQ − xP) |
| yR = yP + t·(yQ − yP). |
![]() X82
X82
Die kartesische Ebene erfüllt die Anordnungsaxiome
II.1 bis II.4.
Beweis:
Seien zwei voneinander verschiedene Punkte (xP; yP)
und (xQ; yQ) beliebig gewählt. Sei ferner t ∈∈ ℝ
und (xR; yR) ein dritter Punkt mit
 |
xR = xP + t·(xQ − xP) |
| yR = yP + t·(yQ − yP). |
(1)
Wird für t ein Wert zwischen 0 und 1 gewählt, so liegt (xR; yR)
zwischen (xP; yP) und (xQ; yQ); ist t größer als 1, so
liegt (xQ; yQ) zwischen (xP; yP) und
(xR; yR); ist t kleiner als 0, so liegt (xP; yP)
zwischen (xR; yR) und (xQ; yQ), entsprechend der Forderung von
Axiom II.2.
(2)
Liegt (xR; yR) zwischen (xP; yP) und
(xQ; yQ), so gilt 0 < t < 1
und man rechnet leicht nach, dass dann mit
t* =def 1 − t auch
 |
xR = xQ + t*·(xP − xQ) |
| yR = yQ + t*·(yP − yQ). |
gilt. Wegen 0 < t* < 1 folgt hiermit, dass (xR; yR) auch zwischen (xQ; yQ) und (xP; yP) liegt, entsprechend der Forderung von Axiom II.1.
(3)
Die Parametrisierung einer Geraden liefert für drei beliebige, aber
voneinander verschiedene Punkte, die auf dieser Geraden liegen, drei reelle Parameterwerte tA, tB und
tC. Die reellen Zahlen sind linear geordnet.
Wenn nun ohne Einschränkung der Allgemeinheit angenommen wird,
dass tA < tB < tC
gilt, so liegt der zu tB gehörende Punkt zwischen den beiden anderen Punkten, entsprechend der Forderung von
Axiom II.3.
(4)
Um die Gültigkeit des Axioms von Pasch nachzuweisen, genügt es
zu zeigen, dass jede Gerade zwei Seiten hat (vgl. X7
und die anschließende Bemerkung).
Hierzu wird festgelegt, dass alle diejenigen Punkte (x; y), für die
ax + by + c < 0 gilt, auf der einen
bzw. alle Punkte (x; y), für
die ax + by + c > 0 gilt,
auf der anderen Seite der Geraden g(a,b,c) liegen sollen.
Die Ordnungsrelation < in ℝ induziert in natürlicher Weise eine Ordnungsrelation in ℝxℝ:
Sei g eine parametrisierte Gerade sowie (xP; yP) und (xQ; yQ) zwei Punkte auf g. Sind tP bzw. tQ die zu (xP; yP) bzw. (xQ; yQ) gehörenden Parameterwerte, so soll
(xP; yP) < (xQ; yQ)
genau dann gelten, wenn tP < tQ gilt.
Gegeben sei eine parametrisierte Gerade g(a,b,c) und ein Punkt (x0; y0) mit
(x0; y0) ∈∈ g(a,b,c).
Dann zerfällt g(a,b,c) stets in drei Teilmengen:
g(a,b,c) = g<0(a,b,c) ∪ { (x0; y0) } ∪ g0>(a,b,c).
Hierbei sind
g<0(a,b,c) =def
{ (x; y) ∈∈ g(a,b,c) | (x; y) < (x0; y0) }
und
g0>(a,b,c) =def
{ (x; y) ∈∈ g(a,b,c) | (x; y) > (x0; y0) }
die von (x0; y0) ausgehenden und zueinander entgegengesetzte Halbgeraden.
(K4) Seien (xp; yp) und (xQ; yQ) zwei voneinander verschiedene Punkte. Dann ist die Strecke PQ gleich der Menge aller Punkte, die zwischen (xp; yp) und (xQ; yQ) liegen.
(K5) Zwei Strecken AB und PQ in der kartesischen Ebene heißen kongruent genau dann, wenn
|(xB; yB) − (xA; yA)| = |(xQ; yQ) − (xP; yP)|.
Nach Definition gilt
|(xB; yB) − (xA; yA)| = √(xB−xA)2 + (yB−yA)2.
|(xB; yB) − (xA; yA)| ist der Abstand zwischen den Punkten (xA; yA) und (xB; yB). Zwei Strecken sind also genau dann kongruent zueinander, wenn die Abstände ihrer jeweiligen Endpunkte gleich groß sind.
![]() X83
X83
Die kartesische Ebene erfüllt die linearen Kongruenzaxiome
III.1 bis III.3.
Beweis:
Gegeben seien eine beliebige Gerade sowie zwei auf dieser
Geraden liegende Punkte (xA; yA), (xB; yB) mit
|(xB; yB) − (xA; yA)| = dAB.
(1)
Sei ferner (xP; yP) ein Punkt auf einer
Geraden g.
Ist g = g(1,0,−c), so
definiert (xP; yP) zusammen mit (xP; yP+dAB)
bzw. mit (xP; yP−dAB)
die zwei einzigen zu AB kongruenten und von (xP; yP)
aus auf den Halbgeraden g<P(1,0,−c) bzw. gP>(1,0,−c)
abgetragenen Strecken. Sei nun g = g(a,b,c) mit b ǂ
0 eine ansonsten beliebig vorgegebene Gerade. Dann ist zu zeigen, dass es
auch in diesem Fall zwei eindeutig bestimmte, auf g liegende Punkte (xQ1; yQ1)
und (xQ2; yQ2) gibt,
derart dass sowohl PQ1 als auch PQ2 kongruent zu AB
ist und zudem (xP; yP) zwischen (xQ1; yQ1)
und (xQ2; yQ2) liegt. Die Bedingung
√(xQ−xP)2 + (yQ−yP)2 = dAB
führt unter Beachtung von
yQ = −abxQ − cb und yP = −abxP − cb
nach längerer Rechnung zur quadratischen Gleichung
xQ2 + p·xQ + q = 0
mit
p = −2·xP und q = xP2·(a2+b2) − dAB2·b2a2+b2.
Diese Gleichung wird gelöst durch
xQ1,2 = xP ± b·dAB√a2 + b2,
womit die gesuchten Punkte (xQ1; yQ1) und (xQ2; yQ2) − wie vom Axiom III.1 gefordert − gefunden sind.
(2)
Gegeben seien drei Punkte (xA; yA), (xB; yB)
und (xC; yC) auf ein und derselben Gerade,
wobei (xB; yB) zwischen (xA; yA)
und (xC; yC)
liegen soll. Dann kann (xB; yB) bezüglich (xA; yA) und (xC; yC)
parametrisiert werden:
 |
xB = xA + t·(xC − xA) |
| yB = yA + t·(yC − yA). |
Hierbei gilt 0 < t < 1. Ersetzt man in
 |
dAB = √(xB−xA)2 + (yB−yA)2 |
| dBC = √(xC−xB)2 + (yC−yB)2 |
xB bzw. yB durch den jeweiligen Summenterm, so ergibt sich
 |
dAB = √t2·√(xC−xA)2 + (yC−yA)2 |
| dBC = √(1−t)2·√(xC−xA)2 + (yC−yA)2 |
und es folgt
dAB + dBC = √(xC−xA)2 + (yC−yA)2.
Man sieht nunmehr sofort, dass Axiom III.3 erfüllt ist.
(3)
Bezüglich Axiom III.2 muss nichts gezeigt werden.
![]() X84
X84
Die kartesische Ebene erfüllt das Archimedische Axiom V.1.
Beweis:
Die Behauptung folgt (nach X81 bis X83)
aus Q12, wonach ℝ ein
archimedisch angeordneter Körper ist.
Angesichts der oben abgeleiteten Formel für das Bogenmaß eines Winkels ist es wenig verwunderlich, wenn nun Folgendes definiert wird:
(K6) Seien h und k zwei voneinander verschiedene, vom Punkt (xV; yV) ausgehende und nicht zueinander entgegengesetzte Halbgeraden. Dann wird durch diese zwei Halbgeraden in analoger Weise zu oben ein Winkel ∠(h,k) definiert.
(K7) Gegeben seien die Winkel ∠(h,k)
und ∠(h’,k’) mit (xP; yP) ∈∈ h
und (xQ; yQ) ∈∈ k
bzw. (xR; yR) ∈∈ h’
und (xS; yS) ∈∈ k’.
(xV; yV) sei der Scheitel von ∠(h,k)
und (xU; yU) der von ∠(h’,k’).
Dann heißen die zwei Winkel ∠(h,k)
und ∠(h’,k’) in der kartesischen Ebene kongruent
genau dann, wenn
⟨(xPV; yPV),(xQV; yQV)⟩|(xPV; yPV)|·|(xQV; yQV)| = ⟨(xRU; yRU),(xSU; ySU)⟩|(xRU; yRU)|·|(xSU; ySU)|.
Hierbei ist
(xPV; yPV) = (xP; yP) − (xV; yV),
(xQV; yQV) = (xQ; yQ) − (xV; yV),
(xRU; yRU) = (xR; yR) − (xU; yU),
(xSU; ySU) = (xS; yS) − (xU; yU)
gesetzt worden.
(K8) Ein durch drei Punkte (xP; yP), (xQ; yQ) und (xV; yV) gegebener Winkel heißt ein rechter Winkel mit (xV; yV) als Scheitel genau dann, wenn
⟨(xPV; yPV),(xQV; yQV)⟩ = 0
gilt.
Alle rechten Winkel in der kartesischen Ebene sind nach Definition kongruent zueinander.
![]() X85
X85
Die kartesische Ebene erfüllt die ebenen Kongruenzaxiome
III.4 bis III.6.
Beweis:
(1)
Aus dem Kosinussatz folgt, dass die Länge der dritten Seite eines
Dreiecks stets eindeutig bestimmt ist, sofern ein Innenwinkel und die Längen der zwei anliegenden Seiten
vorgegeben sind. Demzufolge ist die Aussage des Axioms III.6 für Dreiecke in der
kartesischen Ebene selbstverständlich erfüllt.
(2)
Bezüglich Axiom III.5 muss nichts gezeigt werden.
(3)
Es bleibt noch zu zeigen, dass ein gegebener Winkel nach einer gegebenen Seite an einer gegebenen Halbgeraden
stets auf eindeutig bestimmte Weise abgetragen werden kann. Gegeben sei hierzu ein beliebig gewählter Winkel
∠(h,k) mit dem Scheitel (xV; yV) und zwei Punkten
(xP; yP) ∈∈ h
und (xQ; yQ) ∈∈ k.
Es gelte
⟨(xPV; yPV),(xQV; yQV)⟩|(xPV; yPV)|·|(xQV; yQV)| = W
unter Verwendung der in (K7) eingeführten Abkürzungen. Gegeben sei zudem eine vom Punkt (xU; yU) ausgehende Halbgerade h’ mit (xR; yR) ∈∈ h’. Dann ist die Gleichung
a·(xS−xU) + b·(yS−yU)⟩c·|(xSU; ySU)| = W
zu lösen, wobei (xR−xU) durch a, (yR−yU) durch b und |(xRU; yRU)| durch c ersetzt wurde.
Nach zweckmäßiger Substitution (x = xS−xU und y = yS−yU) sowie den Abkürzungen f = ac und g = bc ergibt sich
f·x + g·y = W·√x2 + y2.
Diese Gleichung liefert unter der Voraussetzung W ǂ f die zwei Lösungen
x = f·g + √W2 − W4W2 − f2·y
x = f·g
− √W2 − W4W2 − f2·y,
die im Fall W ǂ 0 verschieden voneinander sind und die Gleichungen derjenigen Geraden darstellen, auf denen die gesuchten, vom Punkt (xU; yU) ausgehenden Schenkel liegen.
Im Fall W = f ist die Gleichung
W·x + g·y = W·√x2 + y2
zu lösen. Hieraus ergibt sich
x = W2 − g22Wg·y.
Dies ist die Gleichung derjenigen Geraden, auf welcher ein gesuchter Schenkel liegt. Der zweite Schenkel kann unschwer mittels einer Geraden, die senkrecht auf der durch (xU; yU) und (xR; yR) gegebenen Geraden steht, ermittelt werden.
Nach X79 bis X85 kann nunmehr zusammenfassend festgestellt werden:
![]() X86
X86
Die kartesische Ebene erfüllt vollständig das Hilbert’sche Axiomensystem der ebenen euklidischen Geometrie.
Angesichts dieser Tatsache erkennt man die Widerspruchslosigkeit der oben aufgestellten Axiome, denn − formuliert mit Hilberts Worten − „jeder Widerspruch in den Folgerungen aus den Axiomen müßte in der Arithmetik des Systems der reellen Zahlen erkennbar sein“ (Grundlagen der Geometrie, §9). Es ist demnach nicht möglich, durch logische Schlüsse aus den Axiomen eine Tatsache abzuleiten, welche einem der Axiome widerspricht.
![]() X87
X87
Die euklidische Ebene und die kartesische Ebene stehen in einer isomorphen Beziehung zueinander. (vgl.:
isomorphe Mengen)
Beweis:
1. Die Punkte der euklidischen Ebene können den Punkten der kartesischen
Ebene bijektiv einander zugeordnet werden (→ X53).
2. Liegt ein Punkt R zwischen zwei Punkten P und Q, so gilt das Gleiche auch
für die zugeordneten kartesischen Punkte (→ X58, K3): (xR; yR)
liegt dann ebenfalls zwischen (xP; yP) und (xQ; yQ).
Aus diesem Grund ist es so, dass
3. die kartesischen Punkte, die den auf einer euklidischen Geraden liegenden Punkten zugeordnet
sind, ebenfalls auf einer und nur einer Geraden liegen.
4. Sind zwei Strecken AB und CD in der
euklidischen Ebene kongruent zueinander, so gilt dies auch für die diesen zugeordneten Strecken in der kartesischen Ebene
(→ X65, X66, K5).
5. Sind zwei Winkel ∠AVB und ∠CUD
in der euklidischen Ebene kongruent zueinander, so gilt dies auch für die
diesen zugeordneten Winkeln in der kartesischen Ebene. (Ohne Beschränkung der
Allgemeinheit kann nämlich angenommen werden, dass VA ≡ UC
und VB ≡ UD gilt, wonach mit Axiom
III.6 AB ≡ CD
und wegen des Kongruenzsatzes sss
schließlich AVB ≅ CUD folgt. Wegen 3. sind
auch die den Dreiecken AVB und CUD zugeordneten Dreiecke in der kartesischen Ebene kongruent zueinander.)
Abgesehen von der Bezeichnung und der Darstellung der jeweiligen geometrischen Objekte haben nach X87 beide Ebenen und die ihnen zugrundeliegenden Geometrien die gleiche mathematische Struktur und sind diesbezüglich ununterscheidbar.
Die kartesische Ebene, also das kartesische Produkt ℝxℝ (→ K1), hat die Struktur einer Menge (→ Zahlenmengen im Sinne von ZFC). Demnach kann auch die euklidische Ebene als Menge aufgefasst werden.
Die Mengen ℝ und ℝxℝ besitzen dieselbe Mächtigkeit (→ M17). Aufgrund der Isomorphie zwischen der euklidischen und der kartesischen Ebene überträgt sich diese Aussage auf die Geometrie: Jede Gerade in der euklidischen Ebene hat dieselbe Mächtigkeit wie die gesamte Ebene. Anschaulich gesprochen: Auf jeder Geraden befinden sich genauso viele Punkte wie auf der Ebene! Angesichts dieser Erkenntnis, die Georg Cantor als Erster hatte, schrieb dieser in einem Brief am 20. Juni 1877 an Richard Dedekind „Je le vois, mais je ne le crois pas!“ (Ich sehe es, aber ich glaube es nicht!)
Literatur- und Quellenangaben:
Euklid:
Die Elemente, Bücher I bis XIII
Verlag Harri Deutsch, Frankfurt am Main 2010
John Playfair:
Elements of Geometry
W.E. Dean, New York 1846
Moritz Pasch:
Vorlesungen über neuere Geometrie
B. G.Teubner, Leipzig 1882
Eliakim Hastings Moore:
ON THE PROJEKTIVE AXIOMS OF GEOMETRY
in: Transactions of the American Mathematical Society Vol. 3, No. 1 Jan 1902,
pp. 142-158
David Hilbert:
Grundlagen der Geometrie
B. G.Teubner, Leipzig 1903
Richard Baldus:
Nichteuklidische Geometrie
Walter de Gruyter & Co., Berlin und Leipzig 1927
Dieter Neßelmann:
Axiomatische Geometrie
Vorlesung an der Universität Rostock 2010
Herbert Koch:
Elementare und Analytische Geometrie
Vorlesung an der Universität Bonn 2012
Richard Pink:
Geometrie
Vorlesung an der ETH Zürich 2012