Reihe
Im vom indischen Mathematiker und Astronom Nīlakaṇṭha Somayājī um 1500 geschriebenen Werk Tantrasaṅgraha
findet sich eine von Mādhava etwa 100 Jahre zuvor entdeckte Anleitung zur Berechnung der
Kreiszahl π, in heutiger Schreibweise:
π4 = 1 − 13
+ 15
− 17
+ 19
− 111 + −...
Es ist eine der verblüffendsten und schönsten Formeln der Mathematik: π ist nach dieser
Formel darstellbar mit einer alternierenden und nicht abbrechenden Summe aller Bruchzahlen mit ungeraden Nennern. Die Folge der Partialsummen der Mādhava-Reihe
1, 1 − 13, 1 − 13 + 15, 1 − 13 + 15 − 17, ...
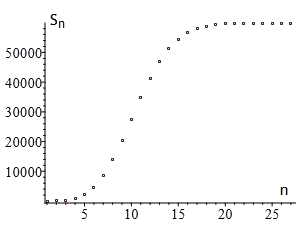
konvergiert leider recht langsam, wie das folgende Diagramm und auch die Tabelle einiger Näherungswerte von π
zeigen.
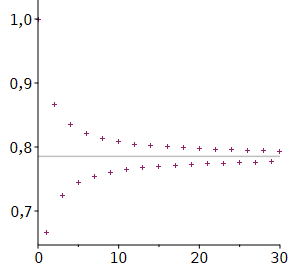
| n | 4·Sn | 4·S(n)π |
| 1 | 2,666666667 | 0,8488263632 |
| 10 | 3,232315809 | 1,028878077 |
| 100 | 3,151493401 | 1,003151506 |
| 1000 | 3,142591654 | 1,000317992 |
| 10000 | 3,141692644 | 1,000031828 |
| 100000 | 3,141602653 | 1,000003183 |
| 1000000 | 3,141593654 | 1,000000318 |
Hierbei ist
Sn = n∑k = 0 (−1)k12k+1.
Auch Gottfried Wilhelm Leibniz hat die Reihe von Mādhava gefunden und 1682 in der Zeitschrift Acta Eruditorum veröffentlicht. Deshalb spricht man heute von der „Mādhava-Leibniz-Reihe“. Um die Gültigkeit der Formel
π = 4·∞∑k = 0 (−1)k12k+1
beweisen zu können, muss man zuvor einen langen und teilweise beschwerlichen Weg zurücklegen, der im folgenden Diagramm stichwortartig skizziert ist:
Die unendliche Summe aller Folgenglieder einer reellen Zahlenfolge (ak)
∞∑k = 0ak = a0 + a1 + a2 + ...
wird Reihe genannt. Die ak heißen Summanden (oder Glieder) dieser Reihe. Die n-ten Partialsummen,
Sn =def n∑k = 0ak für alle n ∈∈ ℕ,
sind die Glieder der Summenfolge der Reihe
∞∑k = 0ak.
Ist die Summenfolge (Sn) einer Reihe konvergent, so heißt die zugehörige Reihe
konvergent. Der Grenzwert von (Sn) wird als Summe der Reihe bezeichnet:
S =lim n→∞Sn =lim n→∞ n∑k = 0ak.
Im Fall der Konvergenz schreibt man einfach: S = ∞∑k = 0ak.
Ist eine Reihe nicht konvergent, so heißt sie divergent.
Beginnt die Nummerierung der Summanden einer Reihe nicht bei 0, sondern bei einer natürlichen Zahl i, die größer als 0 ist, so erhält man Reihen der folgenden Form:
∞∑k = iak = ai + ai+1 + ai+2 + ...
und die obigen Definitionen gelten entsprechend (man ersetze das jeweilige „k = 0“ durch „k = i“).
![]() S1
S1
Ist A die Summe der konvergenten Reihe ∞∑k = 0ak,
B die der konvergenten Reihe ∞∑k = 0bk
und c eine Konstante, dann gelten die folgenden Rechenregeln:
(I) ∞∑k = 0ak +∞∑k = 0bk = ∞∑k = 0(ak + bk) = A + B
(II) ∞∑k = 0ak −∞∑k = 0bk = ∞∑k = 0(ak − bk) = A − B
(III) ∞∑k = 0c·ak = c∞∑k = 0ak = c·A.
Die Aussagen folgen sofort aus den Grenzwertsätzen für Folgen, (i), (iv) bzw. (v).
![]() S2
S2
Wenn eine Reihe konvergent ist, so strebt die Folge ihrer Glieder gegen 0.
Beweis:
Sei S =lim n→∞Sn = ∞∑k = 0ak.
Mit (Sn) ist auch (Sn+1) konvergent. Beide Folgen, (Sn) und (Sn+1), haben denselben Grenzwert. Also ist nach
dem ersten Grenzwertsatz die Folge
(an+1) = (Sn+1)+(−Sn)
eine Nullfolge und damit strebt auch (an) gegen 0.
![]() S3 (Cauchy’sches Konvergenzkriterium für Reihen)
S3 (Cauchy’sches Konvergenzkriterium für Reihen)
Eine Reihe ∞∑k = 0ak
konvergiert genau dann, wenn zu jedem ε > 0
eine natürliche Zahl n0 existiert, so dass
|n∑k = n0+1ak | < ε
für alle n > n0.
Beweis:
Es gilt n∑k = n0+1ak = Sn − Sn0.
Nach dem Cauchy’schen Konvergenzkriterium
konvergiert ∞∑k = 0ak
und damit (Sn) genau dann, wenn es bei vorgegebenem ε > 0 eine natürliche Zahl N gibt, so dass
für alle m,n ≥ N
|Sn − Sm| < ε
gilt. Im Fall der Konvergenz von (Sn) existiert also ein solches N. Mit n0 > N folgt für alle n > n0
|Sn − Sn0| < ε.
Sei nun umgekehrt vorausgesetzt, dass für ein beliebig gewähltes ε > 0 eine natürliche Zahl n0 existiert, so dass für alle n > n0
|Sn − Sn0| < ε2
gilt. Damit hat man für alle n,m > n0
|Sn − Sm|
= |Sn − Sn0 + Sn0 − Sm|
≤ |Sn − Sn0| + |Sm − Sn0|
< ε2
+
ε2
= ε
und hieraus folgt die Konvergenz
von ∞∑k = 0ak.
Mit S3 hat man unmittelbar den folgenden Satz:
![]() S4
S4
Gegeben sei die Reihe ∞∑k = 0ak
und eine beliebige natürliche Zahl n. Dann konvergiert ∞∑k = 0ak
genau dann, wenn ∞∑k = nak
konvergiert.
![]() S5
S5
Gegeben sei eine konvergente Reihe ∞∑k = 0ak
und eine beliebige natürliche Zahl n. Dann gilt
∞∑k = 0ak = n∑k = 0ak +∞∑k = n+1ak .
Beweis:
Es gilt für beliebige natürliche Zahlen m und n
m∑k = 1ak+n =m+n∑k = 0ak −n∑k = 0ak .
Lässt man nun m gegen unendlich streben und beachtet S4 und F2(v), dann ergibt sich
∞∑k = 1ak+n
=∞∑k = 0ak −n∑k = 0ak
und mit ∞∑k = n+1ak =∞∑k = 1ak+n
folgt die Behauptung.
![]() S6
S6
Die harmonische Reihe
∞∑k = 1 1k
ist divergent.
Beweis:
Sei ε = 12 und n0 ∈∈ ℕ beliebig gewählt.
Dann gilt
2n0∑k = n0+1 1k ≥ 2n0∑k = n0+1 12n0 = 12.
Mit S3 folgt die Behauptung.

Am Beispiel der harmonischen Reihe sieht man, dass die Umkehrung vom Satz S2 nicht gilt! Für die Konvergenz einer Reihe ist es nur notwendig, dass die Folge ihrer Summanden gegen 0 strebt, aber nicht hinreichend. Mit anderen Worten: Wenn die Folge der Summanden einer Reihe eine Nullfolge ist, folgt nicht, dass diese Reihe konvergent ist.
Sei x ∈∈ ℝ. Dann heißt
∞∑k = 0xk = 1 + x + x2 + x3 + ....
geometrische Reihe.
![]() S7
S7
Die geometrische Reihe konvergiert gegen
11 − x , falls |x| < 1
und divergiert, falls |x| ≥ 1.
Beweis:
Sei Sn = 1 + x + ... + xn.
Sn lässt sich einfach berechnen, indem die Gleichung Sn = 1 + x + ... + xn mit x multipliziert wird und das Ergebnis von der Ursprungsgleichung abgezogen wird:
Sn − x·Sn = 1 − xn+1 ⇒ Sn = 1 − xn+11 − x.
Sei nun |x| < 1. Dann folgt mit Hilfe der Grenzwertsätze
Sn =
11 − x −
xn+11 − x → 11 − x (n → ∞).
![]() S8
S8
Die Euler’sche Reihe
∞∑k = 01k! = 1 + 11! + 12! + 13! +
...
ist konvergent. Der Grenzwert dieser Reihe ist irrational.
Beweis:
Monoton steigende und nach oben beschränkte Folgen bzw. monoton fallende und
nach unten beschränkte Folgen sind immer konvergent.(→ Beweis).
Nun hat man mit
En =def n∑k = 01k! = 1 + 11! + 12! + 13! +
... + 1n!
erstens eine streng monoton wachsende Summenfolge (En) und zweitens ist die Folge (En) beschränkt. Die untere Schranke su ist 0, die obere Schranke so ist 3, denn es gilt unter Beachtung von S7:
En ≤ 1 + 1 + n−1∑k = 0(12)k = 2 + 1 − 12n1 − 12 < 3.
Der Grenzwert der Euler’schen Reihe, die Euler’sche Zahl, wird mit „e“ bezeichnet.
(En) konvergiert recht rasch, die ersten fünfzehn Folgenglieder (mit 10
Dezimalstellen hinter dem Komma hingeschrieben) lauten:
Angenommen, e ist eine rationale Zahl. Dann gibt
es zwei natürliche Zahlen p und q mit e = pq,
wobei p und q hierbei als teilerfremd vorausgesetzt werden dürfen und es folgt q·e ∈∈ ℕ
mit q ≥ 2 und somit auch q!·e ∈∈ ℕ.
q!·e
= q!·(1 + 11! + ... + 1q! +
1(q+1)! + ...)
= q!·(1 +
11! + ... + 1q!)
+ R
mit
R
= q!·(1(q+1)! + 1(q+2)! + ...)
= (1(q+1)
+ 1(q+1)(q+2) + ...)
= 1q+1·(1
+ 1q+2
+ 1(q+2)(q+3) + ...)
< 1(q+1)·(1
+ 12 + 122 + 123 + ...)
= 2(q+1)
< 1.
Hieraus folgt q!·e ∉∉ ℕ
und damit die Irrationalität von e.
Charles Hermite hat 1873 darüberhinaus bewiesen, dass
e eine transzendente Zahl ist.
![]() S9
S9
Die Zahlenfolge (en), definiert durch
en = (1 + 1n)n für alle n ∈∈ ℕ*
ist konvergent und es gilt en → e (n → ∞).
Beweis:
Sei im Folgenden stets n ∈∈ ℕ*. Mit dem binomischen Lehrsatz und S8 folgt
en
= n∑k = 0(nk)·1nk
= 1 + nn1·1!
+ n·(n−1)n2·2!
+ ... + n·(n−1)·...·2·1nn·n!
≤ 1 + 11! + 12! + 13! +
... + 1n! < 3.
Demnach ist (en) nach oben beschränkt; außerdem ist (en) monoton wachsend. Mit dem Monotoniekriterium folgt die Konvergenz dieser Folge gegen einen Grenzwert g.
Es gilt
en
= 2 + n·(n−1)n2·2! + ... + n·(n−1)·...·2·1nn·n!
= 2 + 12!(1−1n) + ... + 1n!(1−1n)·...·(1 − n−1n)
= n∑k = 0 (1k!·(1 − 1n)·...·(1 − k−1n))
= ∞∑k = 0 (1k!·(1 − 1n)·...·(1 − k−1n)),
denn (1 − 1n)·...·(1 − k−1n)
= 0 für alle k mit k > n.
Also hat man en ≤
∞∑k = 0 1k! =
e für alle n ∈∈ ℕ*.
Sei nun n ∈∈ ℕ*
beliebig, aber fest gewählt und m > n. Mit
S(a,b) =def
b∑k = a (1k!·(1 − 1m)·...·(1 − k−1m))
hat man
em = S(0,n) + S(n+1,m).
Somit gilt
S(0,n) ≤ em ≤ e.
m → ∞
ergibt n∑k = 0 (1k!) ≤
g ≤ e.
Mit n → ∞ folgt
e ≤ g ≤ e und damit die Behauptung.
Das nachfolgende Diagramm illustriert das sehr unterschiedliche Konvergenzverhalten der Folgen (En) (rot) und (en) (blau):

Von Zenon, einem antiken Philosophen des fünften vorchristlichen Jahrhunderts, der in Elea lebte, stammt die folgende Erzählung: Achilleus und eine Schildkröte beabsichtigen, einen Wettlauf zu veranstalten. Unter der Voraussetzung, dass Achilleus der Schildkröte zu Beginn einen gewissen Vorsprung gewährt, argumentiert Zenon nun, dass die langsamere Schildkröte vom schnelleren Achilleus niemals eingeholt werden wird, denn „das Verfolgende muss nämlich zuvor dort ankommen, von wo das Fliehende losgelaufen ist, und so muss das Fliehende immer etwas voraus sein“ (zitiert nach Aristoteles’ Physik, VI. Buch, 9. Kapitel). Dies soll mit der folgenden Zeichnung veranschaulicht werden, wobei hierbei willkürlich angenommen wurde, dass Achilleus (rot) doppelt so schnell ist wie die Schildkröte (grün):
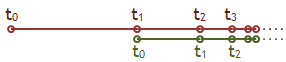
Zur Startzeit t0 laufen beide mit jeweils konstanter Geschwindigkeit los. Wenn Achilleus zur Zeit t1 am Startort der Schildkröte eintrifft, ist die Schildkröte bereits eine bestimmte Strecke voraus gelaufen, und zwar hat sie innerhalb der Zeitspanne t1 − t0 genau die halbe Strecke zurückgelegt im Vergleich zu Achilleus, wenn dieser - wie in diesem Beispiel vorausgesetzt - doppelt so schnell ist als seine Konkurrentin. Und so geht das fortlaufend weiter, denn immer, wenn Achilleus innerhalb einer Zeitspanne tk+1 − tk eine gewisse Strecke zurückgelegt hat, wird die Schildkröte ihm jeweils um die Hälfte dieser Strecke voraus sein.
Nun wird auch Zenon während seines Lebens, höchstwahrscheinlich mehrfach, wahrgenommen haben, dass ein Läufer einen langsameren Läufer bei einem nicht zu großen Vorsprung stets einholt. Dies kann man mit den physikalischen Gesetzen der gleichförmigen Bewegung auch nachrechnen: Der Startzeitpunkt t0 sei gleich 0, d sei der Abstand zwischen Achilleus und der Schildkröte beim Start und x(t) die von der Zeit t abhängige Position von Achilleus bzw. der Schildkröte. Ist vA die Geschwindigkeit von Achilleus und vS die der Schildkröte, dann gilt xA = vA·t und xS = d + vS·t. Für die Position x*, an welcher Achilleus die Schildkröte einholt, gilt vA·t* = d + vS·t* und hieraus ergibt sich nach wenigen Rechenschritten
x* = d·vAvA − vS.
Für die speziellen Positionen xk = x(tk) des Achilleus im obigen Beispiel ist für k = 1,2,3,...
xk+1 − xk = 12·(xk − xk−1).
Allgemein gilt
xk+1 − xk = vSvA·(xk − xk−1).
Das bedeutet, dass sich gemäß der Argumentation von Zenon die Laufstrecke des Achilleus als Reihe darstellen lässt:
d + vSvA·d + (vSvA)2·d + (vSvA)3·d + ... .
d ·∞∑k = 0(vSvA)k
= x*,
eine Formel, die mitnichten das Paradoxon des Zenon erledigt, sondern dessen paradoxe Aussage, der schnellere Achilleus könne (entgegen aller Erfahrung) die langsamere Schildkröte nie einholen, nur auf eine andere - eben formale - Art darstellt. Es ist paradox, dass eine Reihe, die aus unendlich vielen Summanden besteht, einem endlichen Wert gleichgesetzt werden kann! Mit den Worten des Mathematikers und Philosophen Hermann Weyl formuliert: Wenn die Strecke x* wirklich aus unendlich vielen Teilstrecken von der Länge (vSvA)k·d, k= 0,1,2,... „als ‚abgehackten‛ Ganzen besteht, so widerstreitet es dem Wesen des Unendlichen, des ‚Unvollendbaren‛, daß Achilleus sie alle schließlich durchlaufen hat“ (Philosophie der Mathematik und Naturwissenschaft, 8. Auflage, S.61).
Bevor die Summe einer konvergenten Reihe berechnet werden kann, muss zunächst immer erst die Konvergenz der jeweiligen Reihe nachgewiesen werden. Dieser Nachweis gelingt oft mit Hilfe der in diesem Abschnitt vorgestellten Kriterien.
Seien
∞∑k = 0ak
und ∞∑k = 0bk
zwei Reihen mit ak,bk ≥ 0 für alle k ∈∈ ℕ. Gilt dann
ak ≤ bk für
fast alle k (das heißt: ak > bk für
höchstens endlich viele k), so heißt ∞∑k = 0ak
eine Minorante der Reihe ∞∑k = 0bk und
∞∑k = 0bk
eine Majorante von ∞∑k = 0ak.
![]() K1 (Majorantenkriterium)
K1 (Majorantenkriterium)
Jede Minorante einer konvergenten Reihe konvergiert.
Beweis:
Sei ∞∑k = 0ak
eine Reihe mit lauter nichtnegativen Summanden und einer konvergenten Majoranten
∞∑k = 0bk.
Dann gibt es ein κ ∈∈ ℕ, so dass ak ≤ bk für alle k > κ.
Also gilt für alle n mit n > κ
n∑k = κ+1ak ≤ n∑k = κ+1bk ≤ ∞∑k = 0bk = S.
Demnach ist die nach Voraussetzung monoton wachsende Folge (n∑k = 0ak)n=0..∞ durch S +κ∑k = 0ak nach oben beschränkt. Mit dem Monotoniekriterium folgt die Behauptung.
![]() K2 (Quotientenkriterium)
K2 (Quotientenkriterium)
Sei ∞∑k = 0ak
eine Reihe mit lauter positiven Summanden. Wenn es eine Zahl q mit 0 < q < 1
gibt, so dass
ak+1ak ≤ q für fast alle k,
so konvergiert die Reihe. Gilt dagegen
ak+1ak ≥ 1 für fast alle k,
so ist die Reihe divergent.
Beweis:
Gegeben sei die Reihe
∞∑k = 0ak
mit lauter positiven Summanden und der Eigenschaft, dass
ak+1ak ≤ q < 1 für alle k mit k ≥ κ
mit einer gewissen natürlichen Zahl κ. Dann gilt für jede natürliche Zahl m, dass
aκ+m ≤ aκ·qm,
was sich mit vollständiger Induktion über m zeigen lässt: Der Induktionsanfang ist mit aκ+0 ≤ aκ·q0 klar und mit aκ+m ≤ aκ·qm folgt
aκ+m+1 ≤ aκ+m·q ≤ aκ·qm·q = aκ·qm+1.
Somit ist die Reihe ∞∑m = 0aκ·qm
Majorante von ∞∑m = 0aκ+m.
Mit S7 und K1 folgt die Konvergenz von ∞∑m = 0aκ+m
und damit auch die Konvergenz von
∞∑k = 0ak.
Im Fall, dass ak+1ak
≥ 1 für alle k mit k ≥ κ, ist (ak) keine Nullfolge.
Mit S2 folgt die Divergenz von ∞∑k = 0ak.
![]() K3 (Wurzelkriterium)
K3 (Wurzelkriterium)
Sei ∞∑k = 0ak
eine Reihe mit lauter nichtnegativen Summanden. Wenn es eine Zahl q mit 0 < q < 1
gibt, so dass
k√ak ≤ q für fast alle k,
so konvergiert die Reihe. Gilt dagegen
k√ak ≥ 1 für fast alle k,
so ist die Reihe divergent.
Beweis:
Gegeben sei die Reihe
∞∑k = 0ak
mit lauter nichtnegativen Summanden und der Eigenschaft, dass
k√ak ≤ q < 1 für
fast alle k.
Aus k√ak ≤
q folgt ak ≤ qk
und damit hat
∞∑k = 0ak
eine konvergente Majorante, nämlich ∞∑k = 0qk.
Aus k√ak ≥ 1 folgt ak ≥
1, womit die zweite Behauptung folgt.
Sei x irgendeine positive reelle Zahl. Dann konvergiert die Exponentialreihe für x
∞∑k = 0 xkk!,
was man mit dem Quotientenkriterium nachweisen kann: Für alle k > x gilt nämlich
xk+1(k+1)!·k!xk = xk+1 < xx+1 < 1.
Diese Argumentation setzt voraus, dass es immer möglich ist, zu jeder reellen Zahl x eine natürliche Zahl zu finden, die größer als x ist. Dies ist aber der Fall, denn die reellen Zahlen sind archimedisch angeordnet.
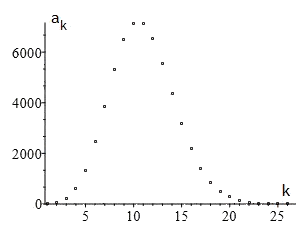
Die folgenden Diagramme zeigen das Verhalten der Summandenfolge (ak)k=0..∞ bzw. der zugehörigen Summenfolge (n∑k = 0ak)n=0..∞ mit ak = xkk! für x = 11.
Sei (ak) eine monoton fallende Folge positiver reeller Zahlen. Dann heißt
∞∑k = 0(−1)kak
eine alternierende Reihe.
![]() K4 (Leibnizkriterium)
K4 (Leibnizkriterium)
Eine alternierende Reihe konvergiert genau dann, wenn die Folge ihrer Summanden eine Nullfolge ist.
Beweis:
Wenn ∞∑k = 0(−1)kak
konvergiert, so folgt lim k→∞(−1)kak = 0 wegen S2.
Sei nun umgekehrt ((−1)kak) eine Nullfolge.
Dann konvergiert nach dem Monotoniekriterium auch (ak) gegen 0.
Die Reihe ∞∑k = 0(−1)kak
lässt sich durch geeignete Zusammenfassung ihrer Glieder auf zwei verschiedene Arten aufschreiben:
(a0 − a1) + (a2 − a3)
+ (a4 − a5) + ...
a0 − (a1 − a2) − (a3 − a4) − (a5 − a6) − ...
Nach Voraussetzung ist (ak) monoton fallend. Es ergeben sich
also nach dieser Idee zwei Teilfolgen der Summenfolge der gegebenen Reihe,
nämlich die monoton steigende Folge (S2k−1)k=1..∞
und die Folge (S2k)k=0..∞, welche monoton fällt. Wegen S2k−1 < S2k < S0
für k=1,2,... ist die erste Teilfolge nach oben
beschränkt, wegen S2k > S2k+1 ≥
S1 für k=0,1,... ist die zweite Teilfolge nach unten beschränkt. Somit
sind beide Teilfolgen konvergent und es gilt
lim k→∞S2k −lim k→∞S2k−1
=lim k→∞(S2k − S2k−1)
=lim k→∞a2k
= 0.
Die Konvergenz der Summenfolge (Sk)k=0..∞
ist damit bewiesen:
S =
lim k→∞Sk =
lim k→∞S2k =
lim k→∞S2k−1
Aus K4 folgt zum Beispiel, dass die alternierende harmonische Reihe
∞∑k = 1(−1)k+11k
konvergiert. Die Konvergenz ist allerdings sehr schlecht, wie das folgende Diagramm zeigt:

Eine Reihe ∞∑k = 0ak
heißt absolut konvergent, wenn die Reihe ∞∑k = 0|ak|
konvergiert.
![]() K5
K5
Eine absolut konvergente Reihe konvergiert.
Sei ∞∑k = 0ak
absolut konvergent, dann konvergiert ∞∑k = 0|ak|.
Es gibt also nach dem Cauchy’schen Konvergenzkriterium zu jedem ε > 0 eine natürliche Zahl n0, so dass
n∑k = n0+1|ak| = |n∑k = n0+1|ak| | < ε
für alle n > n0.
Mit |n∑k = n0+1ak | ≤ n∑k = n0+1|ak| folgt die Behauptung.
![]() K6
K6
Werden in einer absolut konvergenten Reihe beliebig viele Glieder
umgeordnet, so ist auch die neu entstehende Reihe absolut konvergent und die
Summen beider Reihen haben denselben Wert.
Beweis:
Sei ∞∑k = 0ak
eine absolut konvergente Reihe und ∞∑k = 0bk eine Reihe, die genau dieselben
Summanden wie die erstgenannte Reihe besitzt, allerdings in einer anderen Reihenfolge.
Die Summenfolge von∞∑k = 0ak soll (An), die Summenfolge der zweiten Reihe (Bn) heißen.
Sei nun ε > 0 beliebig gewählt, dann gibt es nach dem Cauchy’schen Konvergenzkriterium für Reihen,
angewandt auf ∞∑k = 0|ak|,
eine natürliche Zahl u, so dass
m∑k = u+1|ak| < ε für alle m > u.
In Abhängigkeit von u wähle man nun eine genügend große natürliche Zahl n0, so dass jeder Summand von Au auch Summand von Bn0 ist (Bedingung 1).
Sei nun n ≥ n0. Dann lässt sich eine natürliche Zahl v mit v > n so bestimmen, dass man zu jedem Summanden bk mit u+1 ≤ k ≤ n ein aκ mit u+1 ≤ κ ≤ v finden kann, so dass bk = aκ (Bedingung 2).
Aufgrund der Bedingung 1 folgt
An − Bn =n∑k = 0(ak − bk) =n∑k = u+1(ak − bk).
Jeder Summand von An − Bn ist entweder von der Form „ak“ oder aber (wegen Bedingung 2) von der Form „−aκ“ mit u+1 ≤ κ ≤ v. Somit gilt
|An − Bn| ≤ v∑k = u+1|ak| < ε.
Also ist |An − Bn| < ε
für alle n ≥ n0, gleichbedeutend mit
lim n→∞(An − Bn) = 0.
Aufgrund der Grenzwertsätze
gilt schließlich
lim n→∞Bn
=lim n→∞An −lim n→∞(An − Bn)
=lim n→∞An.
Die Anwendung der gesamten vorstehenden Argumentationskette auf
die Reihen ∞∑k = 0|ak| und
∞∑k = 0|bk| liefert als Ergebnis, dass auch ∞∑k = 0bk
absolut konvergiert.
Der Wert der Summe einer bedingt konvergenten Reihe (also einer konvergenten, aber nicht absolut konvergenten Reihe) ist von der Reihenfolge der Summanden nicht unabhängig! Zum Beispiel gilt
1 − 12 + 13 − 14 + 15 − 16 + 17 − 18 + ... = 0,693147...
1 + 13 − 12 + 15 + 17 − 14 + 19 + 111 − 16 + ... = 1,03972...
Die Ungleichheit beider Summenwerte lässt sich nachweisen, ohne diese numerisch kennen zu müssen:
Teilfolgen einer konvergenten Folge (xn) sind ebenfalls konvergent und streben gegen den Grenzwert von (xn). Also kann man die Summanden einer konvergenten Reihe durch Klammerungen beliebig gruppieren, ohne dass sich am Wert der Summe dieser Reihe etwas ändert, sofern nur die gegebene Reihenfolge der Summanden nicht angetastet wird. So wird zum Beispiel aus
S =∞∑k = 1(−1)k+11k
durch sukzessive Klammerung von jeweils zwei aufeinander folgenden Summanden
(i) S =∞∑k = 1(12k−1 − 12k).
und wenn jeweils vier aufeinander folgende Summanden geklammert werden, erhält man
(ii) S =∞∑k = 1(14k−3 − 14k−2 + 14k−1 − 14k)
Aus (i) folgt mit S1(III)
(iii) S2 =∞∑k = 1(14k−2 − 14k)
und aus (ii) und (iii) ergibt sich mit S1(I)
32S =∞∑k = 1(14k−3 + 14k−1 − 12k),
eine Reihe, die die gleichen Summanden wie die Ausgangsreihe besitzt, nur eben in einer veränderten Reihenfolge.
In diesem Abschnitt sei D stets ein Intervall reeller Zahlen, k eine natürliche Zahl und (fk) eine Folge von auf D definierten reellwertigen Funktionen.
Eine Funktionenfolge (fk) heißt (punktweise) konvergent auf D, wenn für jedes x ∈∈ D (fk(x)) eine konvergente Zahlenfolge ist.
Falls (fk) eine konvergente Funktionenfolge ist, so existiert zu jedem x ∈∈ D der eindeutig bestimmte Grenzwert von (fk(x)) und deswegen auch g, die Grenzfunktion von (fk), auf D definiert durch
g(x) =deflim k→∞fk(x),
und man schreibt dann
g =lim k→∞fk.
Eine Funktionenfolge (fk) ist also genau dann (punktweise) konvergent auf D mit der Grenzfunktion g, wenn es zu jedem x ∈∈ D und zu jedem ε > 0 eine natürliche Zahl k0 gibt, so dass für alle k ≥ k0
|fk(x) − g(x)| < ε
gilt.
Die Vermutung liegt nahe, dass sich gemeinsame Eigenschaften der Glieder einer konvergenten Funktionenfolge automatisch auf die Grenzfunktion dieser Funktionenfolge übertragen. Diese Vermutung erweist sich als falsch, wie das folgende Beispiel zeigt: Mit
fk(x) =def xk für k = 1, 2, 3, ...
hat man eine konvergente Funktionenfolge auf dem Intervall [0, 1]. Alle fk sind stetig auf [0, 1], aber die Grenzfunktion g mit g(x) = 0 für 0 ≤ x < 1 und g(x) = 1 für x = 1 ist offensichtlich nicht stetig.
Es wird sich herausstellen, dass sich die Stetigkeit nur dann auf die Grenzfunktion überträgt, wenn die Funktionenfolge gleichmäßig konvergiert.
Eine Funktionenfolge (fk) konvergiert auf D gleichmäßig gegen ihre Grenzfunktion g, wenn es zu jedem ε > 0 eine natürliche Zahl k0 gibt, so dass für alle k ≥ k0 und für alle x ∈∈ D
|fk(x) − g(x)| < ε
gilt.
Die hier formulierte Bedingung ist leicht zu verwechseln mit der oben im Zusammenhang mit der gewöhnlichen punktweisen Konvergenz hingeschriebenen Bedingung. Man beachte, dass hier die Existenz einer Zahl k0 gefordert wird, welche nur vom vorgegebenen ε abhängt; oben aber ist k0 von ε und vom zuvor gewählten x abhängig. Bei gleichmäßiger Konvergenz gilt die Ungleichung |fk(x) − g(x))| < ε für alle x ∈∈ D gleichermaßen, bei punktweiser Konvergenz gilt diese Ungleichung für das jeweils gewählte (also für das punktuelle) x ∈∈ D, in beiden Fällen natürlich nur für diejenigen k, welche größer oder gleich k0 sind.
![]() G1
G1
Konvergiert eine Funktionenfolge (fk) auf D
gleichmäßig gegen g und sind alle fk in x0 ∈∈ D
stetig, so ist auch g in x0 stetig.
Beweis:
Sei ε > 0 vorgegeben. Nach
Voraussetzung gibt es eine natürliche Zahl k0, so dass für alle k ≥ k0
und für alle x ∈∈ D
|fk(x) − g(x)| < ε3
gilt. Alle fk sind in x0 ∈∈ D
stetig, also auch fk0. Somit gibt es eine
Umgebung U von x0, so dass für jedes x ∈∈ U ∩ D
|fk0(x) − fk0(x0)| < ε3
ist. Aufgrund der Regeln, die für Absolutbeträge in ℝ
gelten, gilt für alle x ∈∈ U ∩ D:
|g(x) − g(x0)|
= |g(x) − fk0(x) + fk0(x) − fk0(x0) + fk0(x0) − g(x0)|
≤ |g(x)−fk0(x)| + |fk0(x)−fk0(x0)| + |fk0(x0)−g(x0)|
< ε3 +
ε3 +
ε3
= ε.
Hiermit folgt die Stetigkeit von g in x0.
![]() G2
G2
Sei (fk) eine auf D gleichmäßig gegen g
konvergente Folge. Jede der Funktionen fk
sei in x0 ∈∈ D
stetig. Dann gibt es zu jedem ε > 0 eine Umgebung
U von x0 und eine natürliche Zahl k0,
so dass für x ∈∈ U ∩ D
und k ≥ k0
|fk(x) − f(x0)| < ε
gilt.
Beweis:
Sei ε > 0
vorgegeben. Aufgrund der im Satz genannten Voraussetzungen ist die Grenzfunktion g gemäß G1
in x0 stetig. Also gibt es eine
Umgebung U von x0, so dass für jedes x ∈∈ U ∩ D
|f(x) − f(x0)| < ε2
ist. Wegen der gleichmäßigen Konvergenz von (fk) gibt es zum vorgegebenen ε eine natürliche Zahl k0, so dass für k ≥ k0 und alle x ∈∈ D
|fk(x) − f(x)| < ε2
gilt. Damit folgt wegen
|fk(x) − f(x0)| ≤ |fk(x) − f(x)| + |f(x) − f(x0)|
die Behauptung.
Die Definitionen und Aussagen über Funktionenfolgen gelten in entsprechender Weise auch für Funktionenreihen:
Eine Funktionenreihe ∞∑k = 0fk heißt konvergent,
wenn die Summenfolge (n∑k = 0fk)n=0..∞
punktweise konvergiert. Falls ∞∑k = 0fk
eine konvergente Funktionenreihe ist, so existiert die eindeutig bestimmte Grenzfunktion s von
(n∑k = 0fk).
s heißt auch „Grenzfunktion von ∞∑k = 0fk“
und man schreibt dann
s =lim n→∞n∑k = 0fk =∞∑k = 0fk.
Eine Funktionenreihe heißt gleichmäßig konvergent, wenn ihre Summenfolge gleichmäßig konvergiert.
Gemäß der Definition der gleichmäßigen Konvergenz für Funktionenfolgen
konvergiert eine Reihe ∞∑k = 0fk
genau dann gleichmäßig auf D gegen s, wenn es zu jedem ε > 0
eine natürliche Zahl n0 gibt, so dass für alle n ≥ n0
und für alle x ∈∈ D
| s(x) − n∑k = 0fk(x) | < ε
gilt. Wenn eine Funktionenreihe ∞∑k = 0fk
gleichmäßig auf D gegen s konvergiert und alle
fk in x0 ∈∈ D stetig sind, so ist wegen
G1 ihre Grenzfunktion s ebenfalls in x0 stetig.
![]() G3 (Cauchy-Kriterium für die gleichmäßige Konvergenz einer Funktionenreihe)
G3 (Cauchy-Kriterium für die gleichmäßige Konvergenz einer Funktionenreihe)
Die Funktionenreihe ∞∑k = 0fk
konvergiert genau dann gleichmäßig auf D, wenn es zu jedem ε > 0
eine natürliche Zahl n0 gibt, so dass für alle n > n0
und für alle x ∈∈ D
|n∑k = n0+1fk(x) | < ε
gilt.
Beweis:
„⇒“: Es sei vorausgesetzt, dass
∞∑k = 0fk
gleichmäßig gegen s konvergiert. Sei ε > 0,
aber ansonsten beliebig vorgegeben. Dann gibt es eine natürliche Zahl n0, so dass für alle n ≥ n0
und für alle x ∈∈ D
| s(x) − n∑k = 0fk(x) | < ε
gilt. Hiermit folgt für alle n, die größer als n0 sind:
|n∑k = n0+1fk(x) |
= | n∑k = 0fk(x) −n0∑k = 0fk(x) |
= | n∑k = 0fk(x) − s(x) + s(x) −n0∑k = 0fk(x) |
≤ | s(x) −n∑k = 0fk(x) | + | s(x) −n0∑k = 0fk(x) |
< ε2 + ε2
= ε.
„⇐“: Sei angenommen, dass es zu einer beliebigen positiven Zahl ε4 eine natürliche Zahl n0 gibt, so dass für alle n > n0 und für alle x ∈∈ D
(*) |n∑k = n0+1fk(x) | <
ε4
gilt. Dann konvergiert die Reihe
∞∑k = 0fk gemäß S3
punktweise gegen eine Grenzfunktion s und es ist „nur“ noch zu zeigen, dass diese Reihe
auch gleichmäßig konvergiert. Man betrachte hierzu die Folge (hm), definiert durch
hm =def |n+m∑k = n+1fk(x) |.
Wegen (*) lässt sich hm wie folgt abschätzen:
hm
= | n+m∑k = n0+1fk(x) − n∑k = n0+1fk(x) |
≤ | n+m∑k = n0+1fk(x) | + | n∑k = n0+1fk(x) |
< ε2.
Mit S5 folgt ∞∑k = 1fk+n(x)
=∞∑k = 0fk(x) −n∑k = 0fk(x) und damit
∞∑k = n+1fk(x)
= s(x) −n∑k = 0fk(x).
Die auf ℝ definierte Betragsfunktion ist überall stetig, also liefert das Folgenkriterium
lim m→∞hm(x)
= | s(x) −n∑k = 0fk(x) |.
Es folgt | s(x) −n∑k = 0fk(x) |
≤ ε2,
was zu beweisen war.
Eine Funktionenreihe ∞∑k = 0fk konvergiert absolut auf D, wenn
∞∑k = 0|fk(x)|
für alle x ∈∈ D konvergiert.
![]() G4
G4
Eine absolut konvergente Funktionenreihe konvergiert und eine sowohl absolut als auch gleichmäßig
konvergente Funktionenreihe konvergiert gleichmäßig.
Wegen
|n∑k = n0+1fk(x) |
≤ n∑k = n0+1| fk(x)
ergeben sich beide Aussagen unmittelbar aus dem Vorhergehenden.
Es folgen ein paar Beispiele für gleichmäßig konvergente und für nur punktweise konvergente Funktionenreihen.
Beispiel 1.
Die geometrische Reihe konvergiert auf dem offenen Intervall (−1, 1) punktweise und nach S7 gilt
∞∑k = 0xk
= 11 − x.
Wegen |xk| = |x|k für k = 0,1,2,...
konvergiert die Reihe auf (−1, 1) auch absolut.
Allerdings konvergiert ∞∑k = 0xk
dort nicht gleichmäßig: Man wähle zwei natürliche Zahlen n0 und b beliebig aus, wobei b nur größer als 0 sein muss.
Es gilt
∞∑k = n0+1xk
= xn0+1·∞∑k = 0xk
= xn0+11 − x.
Sei nun ε = 1b, m = n0+1 und x* = b−1/m , dann folgt
| ∞∑k = n0+1x*k |
= 1b · 11 − x* > 1b.
Aber: ∞∑k = 0xk
konvergiert gleichmäßig auf jedem abgeschlossenen Intervall [−r, r] sofern 0 < r < 1, denn dann gilt für jedes n und unabhängig von x
| ∞∑k = n+1xk |
≤ rn+11 − r.
Weil (rn+11 − r)
eine Nullfolge ist, folgt mit G3 die
gleichmäßige Konvergenz von ∞∑k = 0xk auf [−r, r].
Beispiel 2.
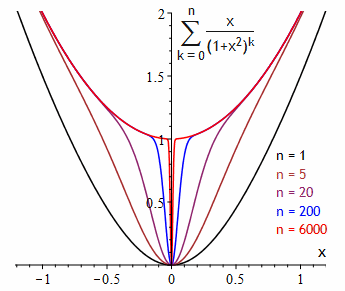
Die Summenfolge (n∑k = 0 x(1+x2)k)
ist nicht gleichmäßig konvergent.
Beispiel 3.
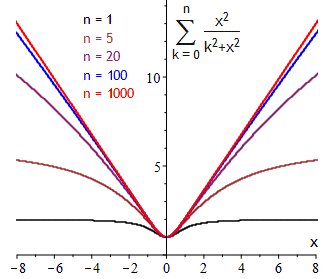
Die Summenfolge (n∑k = 0 x2k2+x2)
konvergiert in jedem abgeschlossenen reellen Intervall gleichmäßig, konvergiert aber auf
ganz ℝ nur punktweise.
![]() G5 (Weierstraß’sches Majorantenkriterium)
G5 (Weierstraß’sches Majorantenkriterium)
Sei ∞∑k = 0ak
eine konvergente Reihe mit lauter nichtnegativen Summanden und
∞∑k = 0fk
eine Reihe von auf D definierten Funktionen. Wenn dann für jedes x ∈∈ D und fast alle k
|fk(x)| ≤ ak
gilt, so konvergiert ∞∑k = 0fk
absolut und gleichmäßig auf D.
Beweis:
Sei ε > 0 beliebig vorgegeben. Dann gibt es
nach Voraussetzung eine natürliche Zahl n0, so dass
für jedes x ∈∈ D
und für alle n > n0
n∑k = n0+1ak < ε und |fn(x)| ≤ an
gilt. Also ist
n∑k = n0+1|fk(x)| ≤ n∑k = n0+1ak < ε
und deshalb folgt mit dem Cauchy’schen Konvergenzkriterium, dass
∞∑k = 0|fk(x)|, also auch
∞∑k = 0fk,
gleichmäßig konvergiert.
Sei x0 eine fest gewählte reelle Zahl und (ak) eine Folge reeller Zahlen. Dann heißt
eine Reihe der Form ∞∑k = 0ak(x − x0)k Potenzreihe mit
den Koeffizienten ak. Man nennt x0 den Entwicklungspunkt der Potenzreihe.
Die geometrische Reihe ist die einfachste Potenzreihe. Sie hat den Entwicklungspunkt 0 und alle ihre Koeffizienten sind gleich 1. Diese Reihe konvergiert absolut im Intervall (−1, 1), absolut und gleichmäßig in jedem abgeschlossenen Teilintervall von (−1, 1) und divergiert außerhalb von [−1, 1] (siehe Beispiel 1). Diese Konvergenzeigenschaften sind typisch für alle Potenzreihen, wie sich gleich zeigen wird.
![]() P1
P1
Wenn eine Potenzreihe ∞∑k = 0ak(x − x0)k
für einen Wert x1 konvergiert, so konvergiert sie absolut für jedes x mit
|x − x0| < |x1 − x0|.
Für jedes x mit dieser Eigenschaft gibt es zwei positive reelle Zahlen s
und q mit q < 1, so dass für alle k
|ak|·|(x − x0)k| ≤ s·qk
gilt. Hierbei kann − falls x1 ǂ x0 und x ǂ x0 ist −
q = |x − x0x1 − x0|
gesetzt werden. s ist von x unabhängig.
Beweis:
Sei ∞∑k = 0ak(x1 − x0)k konvergent. Dann
ist wegen S2 die Folge der Summanden dieser Reihe eine Nullfolge und somit beschränkt (vgl. Q19).
Es gibt also eine positive Zahl s, so dass für alle k
|ak(x1 − x0)k| ≤ s
gilt. Man betrachte nun ein x mit
|x − x0| < |x1 − x0| und x1 ǂ x0.
Dann ist
|x − x0x1 − x0| = q < 1.
und es folgt für alle k
| ak(x − x0)k |
= | ak(x1 − x0)k(x − x0x1 − x0)k |
= | ak(x1 − x0)k |·| x − x0x1 − x0 |k
≤ s·qk.
Die Reihe ∞∑k = 0s·qk konvergiert
wegen S7 und S1(III).
Mit dem Majorantenkriterium folgt die Behauptung.
Sei M die Menge aller (x − x0), für die die Potenzreihe
∞∑k = 0ak(x − x0)k
konvergiert (M ist wegen x0 ∈∈ M nicht leer) und sei s ein Wert, für den die Potenzreihe nicht konvergiert.
Wegen P1 ist dann s eine obere Schranke von M und es existiert das eindeutig
bestimmte Supremum von M, der so genannte Konvergenzradius
dieser Potenzreihe.
Besitzt die Potenzreihe ∞∑k = 0ak(x − x0)k
einen von 0 verschiedenen Konvergenzradius r, dann heißt das offene und in Bezug auf x0
symmetrische Intervall
K = { x: |x − x0| < r }
das Konvergenzintervall dieser Potenzreihe.
Nach dem Beweis von P1 lässt sich nunmehr zusammenfassend Folgendes sagen:
![]() P2
P2
Wenn vom trivialen Fall x = x0 abgesehen wird, konvergiert eine Potenzreihe
∞∑k = 0ak(x − x0)k
nirgendwo (dann setzt man r = 0), oder sie konvergiert innerhalb des Konvergenzintervalls
(x0 − r, x0 + r) absolut und divergiert außerhalb des abgeschlossenen Intervalls
[x0 − r, x0 + r], oder sie konvergiert für alle
reellen Zahlen (in diesem Fall wird r = ∞ gesetzt).
Sowohl für x0 − r als auch für x0 + r
kann man keine allgemeingültige Aussage treffen.
Ist r > 0, so gibt es zu jedem
positiven r1 < r ein s > 0, so dass für alle x
mit |x − x0| < r1 und jedes k
| ak||x − x0|k ≤ s·qk
gilt, wobei q = |x − x0|r1.
Darüberhinaus gilt der folgende Satz:
![]() P3
P3
Ist der Konvergenzradius einer Potenzreihe ∞∑k = 0ak(x − x0)k größer als 0, so konvergiert diese in jedem abgeschlossenen Teilintervall des
Konvergenzintervalls K absolut und gleichmäßig.
Beweis:
Sei K* ein beliebig gewähltes, abgeschlossenes Teilintervall vom Konvergenzintervall K einer Potenzreihe.
Dann gibt es reelle Zahlen r1 und r2 mit
0 < r2 < r1 < r,
so dass
K* ⊂ [x0 − r2, x0 + r2].
Wegen x0 + r1 ∈∈ K konvergiert die Potenzreihe für x0 + r1. Ersetzt man im Beweis von P1 x1 durch x0 + r1, so folgt für alle x mit |x − x0| < r2
| ak(x − x0)k |
≤ s·qk,
wobei q ≤ r2r1 < 1 gilt und die Zahl s nur von r1 und nicht von x abhängt. Mit dem Weierstraß’schen Majorantenkriterium folgt die Behauptung.
Mit G1 folgt unmittelbar
![]() P4
P4
Hat eine Potenzreihe einen positiven Konvergenzradius, so ist die Grenzfunktion dieser Reihe
auf dem Konvergenzintervall stetig.
![]() P5 (Satz von Cauchy-Hadamard)
P5 (Satz von Cauchy-Hadamard)
Sei ∞∑k = 0ak(x − x0)k
eine Potenzreihe mit dem Konvergenzradius r.
Falls die Folge (k√|ak|)k=1..∞
gegen 0 strebt, so ist r = ∞;
konvergiert diese Folge gegen eine positive Zahl g, so gilt r = 1g;
falls limk→∞k√|ak| = ∞
gilt, so ist r = 0.
Beweis:
Die reelle Zahl x0 sei beliebig, aber fest gewählt.
Unter der Voraussetzung, dass limk→∞k√|ak|
existiert, existiert für alle x ∈∈ ℝ mit x ǂ x0
auch |x − x0|·limk→∞k√|ak|
und dann gilt mit g =def limk→∞k√|ak| wegen F2(iv)
limk→∞k√|ak·(x − x0)k| = |x − x0|·g.
Ist g gleich 0, so gibt es ein q mit 0 < q < 1, so dass für fast alle k
k√|ak·(x − x0)k| < q
gilt und es folgt mit dem Wurzelkriterium die absolute Konvergenz der Reihe
∞∑k = 0ak(x − x0)k
für alle x ∈∈ ℝ.
Sei nun 0 < g < ∞ und
|x − x0| < 1g.
Dann folgt
limk→∞k√|ak·(x − x0)k| < 1
und auch hier unter Benutzung des Wurzelkriteriums die absolute Konvergenz der gegebenen Reihe für |x − x0| < 1g.
Für |x − x0| ≥ 1g liefert das Wurzelkriterium dagegen die Divergenz der Reihe.
Im Fall, dass limk→∞k√|ak| = ∞ gilt,
ist die Folge (k√|ak|)
nicht beschränkt. Unter der Voraussetzung, dass x ǂ x0,
ist auch (k√|ak·(x − x0)k|)
und demzufolge auch (|ak·(x − x0)k|) nicht beschränkt, also muss die Reihe
∞∑k = 0ak(x − x0)k
divergieren.
Es folgen einige Beispiele von Potenzreihen.
Der Konvergenzradius der Reihe ∞∑k = 0(k·x)k
ist offensichtlich gleich 0, dagegen konvergiert die Exponentialreihe für alle reellen Zahlen. Die geometrische Reihe hat den Konvergenzradius 1 und konvergiert
weder für x = 1 noch für x = −1.
Die Reihe ∞∑k = 1xkk
hat den Konvergenzradius 1 und konvergiert für x = −1, divergiert jedoch für
x = +1. Die Reihe
∞∑k = 1 xkk2
hat ebenfalls den Konvergenzradius 1 und konvergiert sowohl für x = −1
als auch für x = +1.
Beweis:
(i)
Es gilt limk→∞k√k = 1
(→ Beweis).
Zusammen mit dem Satz von Cauchy-Hadamard folgt r = 1 für die Reihe
∞∑k = 1xkk.
Diese Reihe wird für x = 1 zur harmonischen Reihe, welche divergiert.
Im Fall, dass x = −1, gilt
∞∑k = 1xkk
= −1 + 12
− 13
+ 14
− 15
+ ...
und diese alternierende Reihe konvergiert nach dem Leibnizkriterium.
(ii)
Nach kurzer Rechnung sieht man, dass für den Quotienten q aufeinander folgender Summanden der Reihe
∞∑k = 1 xkk2
q = x1+R(k)
gilt, wobei R(k) → 0 (k → ∞).
Mit dem Quotientenkriterium folgt die Divergenz dieser Reihe für x > 1.
Für |x| < 1 und k = 1,2,3,... gilt
|x|kk2 ≤ |x|k.
(iii)
Da die geometrische Reihe für |x| < 1 konvergiert, folgt mit dem
Majorantenkriterium, dass auch die Reihe ∞∑k = 1 xkk2
für |x| < 1 konvergiert. Mit P2 folgt r = 1.
Für alle n > 1 gilt
Sn
= n∑k = 1 1k2
≤ 1 + n∑k = 2 1k(k−1)
= 1 + n∑k = 2 (1k−1 − 1k)
= 1 + 1 − 1n
< 2.
Also ist die monoton wachsende Summenfolge (Sn) nach oben beschränkt und damit nach
dem Monotoniekriterium konvergent. Hieraus folgt die Konvergenz von
∞∑k = 1 xkk2
für x = 1, als auch für x = −1.
Eine Potenzreihe ist im Innern ihres Konvergenzintervalls differenzierbar. Die Ableitung einer Potenzreihe erhält man durch gliedweises Differenzieren. Um dies beweisen zu können, wird zunächst der folgende Satz benötigt:
![]() P6
P6
Sei D ein Intervall und (fk) eine Folge von auf D
differenzierbaren Funktionen. Alle Ableitungen
fk’ seien stetig auf D. Wenn dann (fk)
gegen g konvergiert und (fk’)
gegen g* gleichmäßig konvergiert, so ist g differenzierbar und es
ist g’ = g*. Das heißt:
Wenn alle hier genannten Voraussetzungen erfüllt sind, so gilt
ddxlim k→∞fk
=
lim k→∞dfkdx.
Beweis:
Sei x0 ∈∈ D
beliebig, aber fest gewählt. Die Grenzfunktion g der konvergenten Funktionenfolge (fk)
ist nach Definition genau dann in x0
differenzierbar, wenn
es auf D eine Funktion Δ gibt mit folgenden Eigenschaften:
| (D1) | Δ ist in x0 stetig. |
| (D2) | g(x) = g(x0) + (x−x0)·Δ(x) für x∈∈D. |
Die durch
Δ(x) =def |
 |
g(x) − g(x0)x − x0
falls x ǂ x0
|
g*(x0) falls x = x0 |
auf D definierte Funktion erfüllt die Bedingung (D2), bleibt also noch zu zeigen, dass Δ in x0 stetig ist.
Sei D* =def D \ { x0 } und
x ∈∈ D*.
Die Funktionen fk sind nach Voraussetzung auf D differenzierbar, also auch auf [x0, x] bzw. auf
[x, x0] stetig. Nach dem ersten Mittelwertsatz der Differentialrechnung
gibt es also für jedes k ein ξk zwischen x0 und x, so dass
fk(x) = fk(x0) + (x − x0)·fk’(ξk).
Mit der für alle k ∈∈ ℕ durch
Δk(x) =def fk(x) − fk(x0)x − x0
auf D* definierten Funktion Δk hat man andererseits
fk(x) = fk(x0) + (x − x0)·Δk(x).
Hiermit folgt Δk(x) = fk’(ξk).
Sei nun ε > 0 vorgegeben. Dann gibt es
nach G2 eine δ-Umgebung
U von x0 und eine natürliche Zahl k0,
so dass für x ∈∈ U ∩ D
und k ≥ k0
|fk’(x) − g*(x0)| < ε2
gilt. Wegen g =lim k→∞fk
gilt aufgrund der Grenzwertsätze auch Δ =lim k→∞Δk.
Somit existiert zu jedem x ∈∈ U ∩ D*
ein k1 ≥ k0, so dass für alle k ≥ k1
|Δ(x) − Δk(x)| < ε2
gilt. Für alle k ≥ k1 folgt nunmehr
unter Beachtung, dass ξk ∈∈ U ∩ D
|Δ(x) − Δ(x0)|
≤ |Δ(x) − Δk(x)| + |Δk(x) − Δ(x0)|
= |Δ(x) − Δk(x)| + |fk’(ξk) − g*(x0)|
≤ ε2
+ ε2
= ε, was zu zeigen war.
Aus P6 folgt unmittelbar
![]() P7
P7
Sei D ein Intervall und (fk) eine Folge von auf D
differenzierbaren Funktionen. Alle Ableitungen fk’ seien stetig auf D. Wenn dann
∞∑k = 0fk
gegen g konvergiert und
∞∑k = 0fk
gleichmäßig konvergiert, so ist g differenzierbar und es gilt
ddx
∞∑k = 0fk
=
∞∑k = 0fk’.
![]() P8
P8
Sei
∞∑k = 0ak(x − x0)k
eine Potenzreihe mit dem Konvergenzintervall K.
Dann ist die durch
f(x) =def ∞∑k = 0ak(x − x0)k
auf K definierte Funktion f differenzierbar und es gilt
f’(x) =∞∑k = 1k·ak(x − x0)k−1.
∞∑k = 1k·ak(x − x0)k−1 besitzt wie die Ursprungsreihe auch das Konvergenzintervall K.
Beweis:
Sei
∞∑k = 0ak(x − x0)k
eine Potenzreihe mit dem von 0 verschiedenen Konvergenzradius r. Dann gibt es positive Zahlen s und q mit
0 < q < 1, so dass für alle k und alle x mit |x − x0| < r
k·| ak(x − x0)k−1 | ≤ s·k·qk−1
gilt (dies entnimmt man dem Beweis von P1).
Die Reihe ∞∑k = 1s·k·qk−1
ist also eine Majorante von
∞∑k = 1k·ak(x − x0)k−1
und konvergiert nach dem Quotientenkriterium. Demnach konvergiert auch
∞∑k = 1k·ak(x − x0)k−1
innerhalb von K. Nach P3 konvergiert diese Reihe zudem gleichmäßig in jedem abgeschlossenen Teilintervall von K.
Unter Beachtung von D10, D11
und D12 folgt mit P7 die Behauptung.
Sei D ein offenes Intervall reeller Zahlen, x0 ∈∈ D
und f eine auf D definierte Funktion. Wenn es dann eine Potenzreihe
∞∑k = 0ak(x − x0)k
gibt, die in einer Umgebung von x0 gegen f konvergiert (man sagt dann: „f ist um x0 in eine Potenzreihe entwickelbar“),
so gilt für x ∈∈ D
f(x) = ∞∑k = 0ak(x − x0)k.
Sei D ein offenes Intervall reeller Zahlen und f eine auf D definierte Funktion. Wenn f um jedes x ∈∈ D in eine Potenzreihe entwickelt werden kann, so heißt f analytisch auf D.
Taylorpolynome und Taylorreihen
![]()
Polynome haben eine übersichtliche Struktur, sind auf ganz ℝ definiert, dort überall differenzierbar und ihre Ableitungen sind einfach (die Ableitung des Polynoms n∑k = 0ak·xk ist nach D10 und D12 gleich n∑k = 1k·ak·xk − 1). Es liegt nahe, sich die Frage zu stellen, ob und − wenn ja − wie und unter welchen Voraussetzungen eine gegebene Funktion mit Hilfe von Polynomen angenähert dargestellt werden kann. Anders gefragt: Kann man (möglicherweise auch komplizierte) Funktionen durch ganzrationale Funktionen approximieren? Der britische Mathematiker Brook Taylor (1685−1731) fand 1712 die Antwort: Ja, das kann man, und zwar mit den nach ihm benannten Taylorpolynomen, sofern die zu approximierende Funktion genügend oft differenzierbar ist.
Sei f eine auf der zulässigen Menge D definierte Funktion
und x0 ∈∈ D.
f heißt n-mal differenzierbar in x0, wenn es eine
Umgebung U von x0 gibt, so dass f(n−1) (die
(n−1)-te Ableitung von f) auf U ∩ D existiert und in x0
differenzierbar ist.
Sei f eine auf D definierte Funktion, x0 ∈∈ D und f in x0 n-mal differenzierbar. Der Wert des Polynoms p(x), welches f innerhalb einer gewissen Umgebung von x0 approximieren soll, wird sicherlich mit dem Funktionswert von f an der Stelle x0 übereinstimmen müssen. Außerdem sollten sich f und p in ihrem Änderungsverhalten an der Stelle x0 möglichst nicht voneinander unterscheiden, das heißt, die jeweiligen Ableitungen von p bzw. f sollten in x0 übereinstimmen. Gesucht ist also ein Polynom n-ten Grades
p(x) = n∑k = 0ak(x − x0)k,
so dass für alle s = 0, 1, ..., n
p(s)(x0) = f(s)(x0)
gilt. Differenziert man p(x) s-mal, dann ergibt sich wegen D12 zusammen mit D10 und D11
p(s)(x) = n∑k = sk·(k−1)·...·(k−(s−1))·ak·(x − x0)k−s
und hieraus folgt für alle s = 0, 1, ..., n
p(s)(x0) = s!·as,
womit das gesuchte Polynom gefunden ist.
Ist f eine in x0 mindestens n-mal differenzierbare Funktion, so heißt
n∑k = 0f(k)(x0)k!(x − x0)k
das n-te Taylorpolynom von f mit Entwicklungspunkt x0. Dieses Polynom soll im Folgenden mit Tn,x0(x) bezeichnet werden.
![]() T1 (Taylor’scher Satz)
T1 (Taylor’scher Satz)
Sei D ein halboffenes Intervall ( [x0, c)
oder (c, x0] ), f eine auf D definierte und in x0 mindestens (n+1)-mal differenzierbare Funktion
und Tn,x0(x) das n-te Taylorpolynom von f mit Entwicklungspunkt x0. Sei ferner U eine Umgebung von x0,
so dass f(n) auf U ∩ D existiert,
x ∈∈ U
und h =def x − x0.
Dann gibt es eine für alle h mit x0 + h ∈∈ D
erklärte, in h = 0 stetige Funktion Δ, so dass Folgendes gilt:
| (i) | Δ(0) = f(n+1)(x0) |
| (ii) | f(x) = Tn(x) + Δ(h)·hn+1(n+1)! |
Beweis:
Sei x ∈∈ U ∩ D
mit x ǂ x0 und sei r(x) =def f(x) − Tn,x0(x).
Dann existiert mit f(n) auch r(n) auf U ∩ D
und es folgt wegen
Tn,x0(s)(x0) = f(s)(x0) für alle s = 1, 2, ..., n
r(x0) = r(s)(x0) = 0.
Es gilt offenbar
r(x)(x − x0)n+1 = r(x) − r(x0)(x − x0)n+1 − (x0 − x0)n+1.
Die Anwendung des zweiten Mittelwertsatzes liefert
r(x)(x − x0)n+1 =
r’(ξ1)(n+1)(ξ1 − x0)n
mit einem gewissen ξ1 zwischen x0 und x. Die weitere sukzessive
Anwendung des zweiten Mittelwertsatzes ergibt schließlich
(*) r(x)(x − x0)n+1 =
r(n)(ξn)(n+1)!(ξn − x0)
mit einem ξn zwischen x0 und ξn−1
und damit erst recht zwischen x0 und x. Es gibt also ein tn mit
0 < tn < 1, so dass
ξn = x0 + tn·h.
Nach Voraussetzung ist f(n) differenzierbar in x0, also existiert auch r(n+1)(x0). Es gibt demnach eine in x0 stetige Funktion Δ* mit Δ*(x0) = r(n+1)(x0), für die
r(n)(x) = r(n)(x0) + (x − x0)·Δ*(x)
gilt, und zwar für alle x ∈∈ U ∩ D.
Unter Beachtung von r(n)(x0) = 0 folgt
r(n)(ξn) = (ξn − x0)·Δ*(ξn).
Zusammen mit (*) ergibt sich
r(x) = Δ*(x0 + tn·h)hn+1(n+1)!.
Sei nun für alle h mit x0 + h ∈∈ D die Funktion Δ durch
Δ(h) =def Δ*(x0 + tn·h)
definiert. Mit dem Folgenkriterium lässt sich die Stetigkeit von Δ in h = 0 zeigen: Ist (hk) eine Nullfolge, so auch (tnhk). Also strebt (x0 + tnhk) gegen x0 und, weil Δ* stetig in x0 ist, Δ*(x0 + tnhk) gegen Δ*(x0). Somit strebt (Δ(hk)) gegen Δ(0), wenn (hk) gegen 0 strebt.
Wegen Tn,x0(n+1)(x) = 0 ist r(n+1)(x) = f(n+1)(x) und damit gilt
Δ(0) = Δ*(x0) = f(n+1)(x0).
![]() T2
T2
Existiert f(n+1)(x) unter den Voraussetzungen von T1 nicht nur
für x = x0, sondern darüberhinaus für
alle x ∈∈ U ∩ D,
dann gilt für diese x
f(x) = Tn,x0(x) + Rn(x),
wobei es ein ξ zwischen x und x0
gibt, so dass
Rn(x) = f(n+1)(ξ)·(x − x0)n+1(n+1)!.
Beweis:
Sei x ∈∈ U ∩ D
mit x ǂ x0 und sei r(x) =def f(x) − Tn,x0(x).
Dann existiert mit f(n) auch r(n) auf U ∩ D
und es folgt wegen
Tn,x0(s)(x0) = f(s)(x0) für alle s = 1, 2, ..., n
r(x0) = r(s)(x0) = 0.
Unter diesen Voraussetzungen wurde im Beweis von T1 mittels sukzessiver Anwendung des zweiten Mittelwertsatzes die Formel
(*) r(x)(x − x0)n+1 =
r(n)(ξn)(n+1)!(ξn − x0)
hergeleitet. Ist f überall auf U ∩ D (n+1)-mal differenzierbar,
so lässt sich dieser Satz nochmals anwenden und man erhält
(*) r(x)(x − x0)n+1 =
r(n+1)(ξn+1)(n+1)!
mit
x0 < ξn+1 < x. Die Behauptung folgt unmittelbar.
Das Langrange’sche Restglied Rn(x) ist für x = x0 gleich 0
und lässt sich für x ǂ x0 nach oben abschätzen.
Man nehme hierfür zwei positive Zahlen k und ε, so dass für alle
x ∈∈ U ∩ D
|f(n+1)(x)| < k und |x − x0| < ε
gilt. Dann folgt
|Rn(x)| = |f(x) − Tn,x0(x)| < k·εn+1(n+1)!.
Die Möglichkeit der Approximation einer Funktion durch ihre Taylorpolynome in einer gewissen Umgebung eines vorgegebenen Entwicklungspunktes x0 soll mit der folgenden Animation illustriert werden. Hierzu sei f eine gebrochen-rationale Funktion, definiert durch
f(x) =def 370 + 0,25x3 + 6,5x2 − 108,5x2x2 − 25x + 80,
und x0 = −2,5.
![]() T3
T3
Sei D ein Intervall reeller Zahlen, x0 ∈∈ D, f eine auf D definierte und
in x0 mindestens n-mal differenzierbare Funktion. Sei ferner D* ⊆ D mit
x0 ∈∈ D*
und
p(x) = n∑k = 0ak(x − x0)k
ein Polynom. Existiert dann eine auf D* definierte und in x0 stetige Funktion q, so dass q(x0) = 0 und für x ∈∈ D*
f(x) = p(x) + q(x)·(x − x0)n
gilt, dann folgt ak = f(k)(x0)k! für alle k = 0, 1, ..., n.
Das bedeutet: Wenn es unter den Voraussetzungen dieses Satzes ein Polynom mit den genannten Eigenschaften gibt, dann ist es eindeutig bestimmt, und es ist Tn,x0(x), das n-te Taylorpolynom von f mit Entwicklungspunkt x0. Es gibt demnach keine Polynome, die f in einer vorgegebenen Umgebung genauso gut approximieren wie Tn,x0(x).
Beweis:
(I) Seien f, p(x) = n∑k = 0ak(x − x0)k und q gemäß der im Satz genannten Voraussetzungen gegeben. Es gelte zunächst speziellerweise
f(k)(x0) = 0 für alle
k = 0, 1, ..., n. Dann folgt unter Benutzung von
T1 für alle
x ∈∈ D*
Δ(x − x0)·(x − x0)n(n)! = p(x) + q(x)·(x − x0)n
und hieraus mit v(x) =def Δ(x − x0)(n)! − q(x)
(*) n∑k = 0ak(x − x0)k = v(x)·(x − x0)n.
v ist als Differenz zweier in x0 stetiger Funktionen ebenfalls in x0
stetig und es gilt
v(x0) = 0 wegen Δ(0) = f(n)(x0) = 0
und q(x0) = 0. Die Gleichung (*)
gilt für alle
x ∈∈ D*, also auch für x0.
Hiermit folgt a0 = 0. Nun kann man zeigen, dass ak = 0 auch für
alle k = 1, 2, ..., n
gilt.
Sei hierfür j ≥ 1 so gewählt, dass für alle i
mit i < j ai = 0
gilt. Dann folgt mit (*) für
x ∈∈ D* \ { x0 }
aj + n∑k = j+1ak(x − x0)k−j = v(x)·(x − x0)n−j.
Sämtliche Terme in dieser Gleichung gehören zu in x0 stetigen Funktionen, also gilt die Gleichung auch für x0. Es folgt aj = 0.
Somit folgt aus a0 = 0 zunächst a1 = 0, sodann a2 = 0, und so fort bis an = 0.
(II) Seien wiederum f, p(x) und q gemäß der im Satz genannten Voraussetzungen gegeben, allerdings nun ohne weitere Bedingungen für f. Aus
f(x) = p(x) + q(x)·(x − x0)n
folgt
f(x) − Tn,x0(x) = p*(x) + q(x)·(x − x0)n
mit
p*(x) = n∑k = 0(ak − f(k)(x0)k!)(x − x0)k.
Für alle s = 0, 1, ..., n gilt Tn,x0(s)(x0) = f(s)(x0) und damit p*(s)(x0) = 0. Nach dem Teil (I) dieses Beweises folgt ak = f(k)(x0)k! für alle k = 0, 1, ..., n, was zu beweisen war.
Ist eine Funktion auf einem Intervall unendlich oft differenzierbar, dann kann man dort zu jeder natürlichen Zahl das n-te Taylorpolynom dieser Funktion bilden. Aus diesem Grund ist die folgende Definition sinnvoll:
Sei D ein offenes Intervall reeller Zahlen, x0 ∈∈ D und f eine auf D definierte und in x0 unendlich oft differenzierbare Funktion. Dann heißt die Potenzreihe
∞∑k = 0f(k)(x0)k!(x − x0)k
die Taylorreihe von f mit Entwicklungspunkt x0 (oder: die Taylorreihe von f um x0).
Es folgt zusammen mit T3 und P8 unmittelbar
![]() T4
T4
Sei D ein offenes Intervall reeller Zahlen, x0 ∈∈ D
und f eine auf D definierte Funktion. Ist f um x0 in eine Potenzreihe entwickelbar, dann
ist f in einer Umgebung von x0 unendlich oft differenzierbar und die Potenzreihe ist die Taylorreihe von f um x0.
Ist f analytisch auf D, so ist f auf ganz D unendlich differenzierbar. Alle Ableitungen von f sind ebenfalls analytisch auf D.
![]() T5
T5
Sei D eine zulässige Menge reeller Zahlen, f eine auf D definierte und dort überall unendlich differenzierbare
Funktion und x0 ∈∈ D.
Gibt es dann zwei positive reelle Zahlen σ und δ, so dass für alle k > 0
und x ∈∈ Uδ(x0) ∩ D
|f(k)(x)|k! δk ≤ σ
gilt, so konvergiert die Taylorreihe von f um x0 in Uδ(x0) ∩ D
gegen f.
Beweis:
Sei ε > 0 vorgegeben und
x ∈∈ Uδ(x0) ∩ D.
Da somit |x − x0| kleiner als δ ist, gibt es eine natürliche Zahl n0,
so dass
|x − x0|n0δn0 < εσ.
Für n ≥ n0 gilt dann mit einem gewissen ξ zwischen x und x0
| f(x) − n∑k = 0f(k)(x0)k!(x − x0)k |
= |f(n+1)(ξ)|·|x − x0|n+1(n+1)! (wegen T2)
≤ σ·(n+1)!δn+1·|x − x0|n+1(n+1)!
< σ·εσ
= ε, was zu zeigen war.
![]() T6
T6
Sei ∞∑k = 0ak(x − x0)k eine Potenzreihe mit einem positiven Konvergenzradius r. Dann ist die auf dem Konvergenzintervall K durch
f(x) =def ∞∑k = 0ak(x − x0)k
definierte Funktion f analytisch auf K.
Beweis:
Sei x1 ∈∈ K beliebig,
aber fest gewählt. Weil K ein offenes Intervall ist, gibt es dann ein
r1 mit |x1| < r1 < r.
Für alle k und alle x mit |x − x0| < r1 gibt es wegen P1 bzw. P2 eine positive und von x unabhängige Zahl s, so dass
|ak|·|(x − x0)k| ≤ s·qk
gilt, wobei
q = |x − x0|r1
gesetzt worden ist. Hiermit gilt für alle x mit |x − x0| < r1
und x ǂ x0
|ak+n|·|x − x0|k
= |ak+n||x − x0|k+n|x − x0|n
≤ s·qk·qn|x − x0|n
= s·qkr1n.
Demnach folgt zusammen mit P8 für x mit |x − x0| < r1
|f(n)(x)|
≤ ∞∑k = 0(k+1)·(k+2)·...·(k+n)·|ak+n|·|x − x0|k
≤ sr1n·∞∑k = 0(k+1)·(k+2)·...·(k+n)·qk
= sr1n·n!(1−q)n+1.
Der letzte Schritt bedarf einer Erklärung: Einerseits lässt sich die geometrische Reihe wegen P8 gliedweise n-mal differenzieren, was nach kurzer Rechnung
dndqn∞∑k = 0qk = ∞∑k = 0(k+1)·(k+2)·...·(k+n)·qk
liefert, andererseits ergibt sich wegen S7 zusammen mit P7 nach n-maliger Anwendung der Quotientenregel
dndqn∞∑k = 0qk = n!(1−q)n+1.
Aus |f(n)(x)| ≤ sr1n·n!(1 − q)n+1 folgt schließlich
|f(n)(x)|n!·(r1(1 − q))n ≤ s1 − q.
Sei nun δ =def 12·(r1 − |x1 − x0|). Dann folgt für x ∈∈ Uδ(x1)
δ ≤ r1 − |x − x0| = r1(1 − q),
was durch folgende Figur illustriert wird:

Schlussendlich hat man für x ∈∈ Uδ(x1)
|f(n)(x)|n!·δn ≤ s1 − q.
Da es in jedem Fall ein σ mit s1 − q ≤ σ gibt,
folgt mit T5 die Behauptung, denn x1 ∈∈ K war eingangs beliebig gewählt.
![]() T7 (Identitätssatz für Potenzreihen)
T7 (Identitätssatz für Potenzreihen)
Seien ∞∑k = 0ak(x − x0)k und ∞∑k = 0bk(x − x0)k
zwei Potenzreihen mit gleichem Entwicklungspunkt x0 sowie positiven Konvergenzradien ra bzw. rb.
Sei ferner Uε(x0) eine ε-Umgebung
von x0 mit ε < min(ra, rb)
und f bzw. g durch
f(x) =def ∞∑k = 0ak(x − x0)k und
g(x) =def ∞∑k = 0bk(x − x0)k
auf Uε(x0)
definierte Funktionen. Wenn dann für alle x ∈∈ Uε(x0)
f(x) = g(x) gilt, so
folgt ak = bk für alle k = 0,1,2,..., das heißt, beide Potenzreihen
sind in diesem Fall identisch.
Beweis:
Nach T4 sind f und g auf Uε(x0)
unendlich oft differenzierbar. Damit folgt insbesondere die Stetigkeit von f, g und aller derer Ableitungen und es gilt
für jede natürliche Zahl n und x ∈∈ Uε(x0)
0
= f(x) − g(x)
= ∞∑k = 0(ak − bk)(x − x0)k
wegen S1(II)
= (n∑k = 0(ak − bk)(x − x0)k) + (x − x0)n·q(x)
mit
q(x) = ∞∑k = n+1(ak − bk)(x − x0)k−n.
q ist in x0 stetig und es gilt q(x0) = 0. Mit T3 folgt für alle k = 0,1,2,...
ak = bk
und damit die Behauptung.
Ist f eine ganzrationale Funktion n-ten Grades,
so sind ihr Funktionsterm n∑k = 0ak·xk
und ihr n-tes Taylorpolynom von f mit 0 als Entwicklungspunkt
wegen T2 und T3 identisch.
Das Langrange’sche Restglied Rn(x) ist wegen f(n+1) ≡ 0
gleich 0. Sind x0 und ξ0 beliebige reelle Zahlen, so gilt
für alle x ∈∈ ℝ
f(x) = Tn,x0(x) = Tn,ξ0(x).
Das Polynom n∑k = 0ak·xk kann in jedem Fall in eine Potenzreihe
∞∑k = 0bk·xk
umgewandelt werden, wobei
bk = ak für k = 0,1,2,...,n
bk = 0 für k > n.
Mit T7 folgt, dass alle Koeffizienten ak eindeutig bestimmt sind.
Der Fundamentalsatz der Algebra besagt, dass ein Polynom n-ten Grades höchstens n Nullstellen besitzt. Aus dem folgenden Satz T8 folgt demnach, dass eine auf ganz ℝ definierte ganzrationale Funktion n-ten Grades höchstens (n−1) lokale Extremwerte besitzen kann.
Sei f eine auf D definierte Funktion. Dann besitzt f an der Stelle x0 ∈∈ D ein lokales Maximum bzw. ein lokales Minimum, wenn es eine Umgebung U von x0 gibt, so dass
f(x0) = max { f(x) | x ∈∈ U∩D } bzw.
f(x0) = min { f(x) | x ∈∈ U∩D }
gilt.
![]() T8
T8
Sei D ein offenes Intervall und f eine auf D definierte und dort überall differenzierbare Funktion.
Wenn dann f an der Stelle x0 ein lokales Extremum (also ein lokales Maximum oder ein lokales Minimum) besitzt,
so gilt f’(x0) = 0.
Beweis:
Sei U eine echte Teilmenge von D und eine Umgebung von x0 mit f(x0) = max { f(x) | x ∈∈ U }.
Es wird also vorausgesetzt, dass f an der Stelle x0 ein lokales Maximum besitzt.
Weil f auf D differenzierbar ist, gibt es eine in x0 stetige Funktion Δ, so dass
für x ∈∈ U
f(x) = f(x0) + (x − x0)·Δ(x)
gilt.
Angenommen, es ist Δ(x0) > 0. Dann gibt es wegen der Stetigkeit von Δ in x0 eine Umgebung U1 von x0, so dass für alle x ∈∈ U1 Δ(x) > 0 gilt. Damit folgt für x ∈∈ U1 mit x > x0 f(x) > f(x0) und dies ist ein Widerspruch zur Voraussetzung!
Angenommen, es ist Δ(x0) < 0. Dann gibt es eine Umgebung U2 von x0, so dass für alle x ∈∈ U2 Δ(x) < 0 gilt. Damit folgt für x ∈∈ U2 mit x < x0 wiederum f(x) > f(x0) und damit wieder ein Widerspruch zur Voraussetzung.
Somit folgt f’(x0) = Δ(x0) = 0. Hat f an der Stelle x0 ein lokales Minimum, so besitzt −f dort ein lokales Maximum und es folgt −f’(x0) = 0 und damit auch f’(x0) = 0.
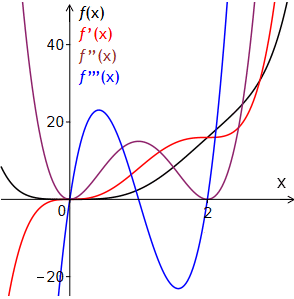
Das folgende Diagramm zeigt die Schaubilder einer ganzrationalen Funktion f und ihrer ersten, zweiten und dritten Ableitung. Es ist insbesondere ein Beispiel dafür, dass die Umkehrung von T8 nicht gültig ist. Hierfür wurde definiert: f(x) =def 12x6 − 3x5 + 5x4.
![]() T9
T9
Sei f eine in einer Umgebung Uδ(x0)
differenzierbare Funktion.
Sei ferner Ulinks = (x0 − δ, x0) und
Urechts = (x0, x0 + δ).
Dann besitzt f an der Stelle x0 genau dann ein lokales Minimum, wenn für
x ∈∈ Ulinks f’(x) ≤ 0
und für x ∈∈ Urechts f’(x) ≥ 0 gilt.
f besitzt an der Stelle x0 genau dann ein lokales Maximum, wenn für
x ∈∈ Ulinks f’(x) ≥ 0 und für
x ∈∈ Urechts f’(x) ≤ 0 gilt.
Dies bedeutet, dass f an einer Stelle x0 dann und nur dann ein Extremum besitzt, wenn f’(x) beim Durchgang durch x0 das Vorzeichen wechselt.
Beweis:
Es sei |h| < δ. Dann folgt aus dem ersten Mittelwertsatz
D13(I)
f(x0 + h) − f(x0) = h·f’(x0 + ϑ·h),
wobei ϑ eine reelle Zahl mit
0 < ϑ < 1 darstellt.
f besitzt also an der Stelle x0 genau dann ein Extremum, wenn
f(x0 + h) − f(x0)
für alle h mit |h| < δ und h ǂ 0
dasselbe Vorzeichen hat. Hieraus folgt ohne Weiteres die Richtigkeit der behaupteten Aussagen.
![]() T10
T10
Sei f eine in x0 n-mal differenzierbare Funktion. Sei ferner
f(k)(x0) = 0 für
k = 1,2,...,n−1
sowie f(n)(x0) ǂ 0. Wenn n ungerade ist, so hat f an der Stelle
x0 kein lokales Extremum. Ist n gerade, so hat f an der Stelle x0 ein lokales Minimum falls
f(n)(x0) > 0, bzw. ein lokales Maximun falls
f(n)(x0) < 0 ist.
Beweis:
Mit dem Taylor’schen Satz folgt unter den genannten Voraussetzungen
f(x0 + h) − f(x0) = Δ(h)·hnn!
mit einer in 0 stetigen Funktion Δ, für die Δ(0) = f(n)(x0) gilt.
Wegen der Stetigkeit von Δ an der Stelle 0 haben Δ(h), Δ(−h) und f(n)(x0) gleiche Vorzeichen, falls |h| genügend klein gewählt wird.
Wenn nun n ungerade ist, so ist hn und damit auch f(x0 + h) − f(x0) für h > 0 positiv und für h < 0 negativ. f hat in diesem Fall also kein Extremum an der Stelle x0. Ist dagegen n gerade, so ist hn für alle h ǂ 0 positiv. Ist also f(n)(x0) und damit auch Δ(h) positiv, so besitzt f an der Stelle x0 ein lokales Minimum, ist f(n)(x0) und damit auch Δ(h) negativ, so besitzt f an der Stelle x0 ein lokales Maximum.
Nicht-algebraische elementare Funktionen
![]()
Eine Funktion von ℝ nach ℝ wird in der Regel dann als elementar bezeichnet, wenn sie zu einer der folgenden Funktionenklassen gehört: ganzrationale Funktionen (einschließlich der konstanten Funktionen und der Potenzfunktionen), exponentielle und logarithmische Funktionen, trigonometrische Funktionen und deren Umkehrfunktionen, hyperbolische Funktionen und deren Umkehrfunktionen. Eine Funktion heißt auch dann elementar, wenn sie sich aus den genannten Funktionen in endlich vielen Schritten durch Addition, Subtraktion, Multiplikation, Division oder Verkettung erzeugen lässt.
Einige der wichtigsten nicht-algebraischen elementaren Funktionen, nämlich exp, ln, sin, cos, tan, arcsin, arccos und arctan, sollen im Folgenden diskutiert werden.
Die natürliche Exponentialfunktion
Die Konvergenz der Exponentialreihe wurde bereits für positive Werte für x mithilfe des Quotientenkriteriums bewiesen. Demnach konvergiert diese Reihe absolut und mit K5 folgt die Konvergenz der Exponentialreihe für alle x ∈∈ ℝ, so dass folgende Definition möglich ist:
Die auf ganz ℝ durch
exp(x) =def
∞∑k = 0 xkk!
definierte Funktion heißt natürliche Exponentialfunktion.
![]() L1
L1
Es gilt
exp’ = exp.
Beweis:
Mit P7 folgt
exp’(x) = ∞∑k = 0 1k!d(xk)dx
= ∞∑k = 1 xk−1(k−1)!
= ∞∑k = 0 xkk!
= exp(x).
Ist c eine Konstante, so folgt aus L1 zusammen mit der Faktorregel, dass auch
(c·exp(x))’ = c·exp(x)
gilt.
![]() L2 (Additionstheorem der Exponentialfunktion)
L2 (Additionstheorem der Exponentialfunktion)
Für alle x1,x2 ∈∈ ℝ gilt
exp(x1 + x2) = exp(x1)·exp(x2).
Beweis:
Sei D ein abgeschlossenes Intervall. Dann gibt es für alle x ∈∈ D
ein σ, so dass |exp(x)| < σ. Wegen L1 gilt ebenso
|exp(k)(x)| < σ, und zwar für alle k.
Außerdem folgt mit S2, dass (δkk!)
für jede beliebige positive Zahl δ eine Nullfolge ist. Es gilt also für alle x ∈∈ D
und für genügend große k
|exp(k)(x)|k!·δk < σ·δkk! < σ.
Sei nun x0 ∈∈ D. Dann konvergiert wegen T5 die Taylorreihe von exp um x0 in D gegen exp. Für D gelten keinerlei Einschränkungen, also konvergiert die Taylorreihe von exp um ein beliebig zu wählendes x0 überall gegen exp, so dass mit h = x − x0 folgende Rechnung aufgemacht werden kann:
exp(x) = exp(x0 + h) = ∞∑k = 0exp(k)(x0)k!hk
= exp(x0)·∞∑k = 0hkk! = exp(x0)·exp(h).
Aus L2 folgt unmittelbar
exp(0) = 1 und
exp(x)·exp(−x) = 1.
Die Funktion exp nimmt also auf ganz ℝ niemals den Wert 0 an. Gäbe es ein x mit exp(x) < 0, so müsste es wegen exp(0) > 0 nach dem Zwischenwertsatz mindestens eine Nullstelle von exp geben: Widerspruch! Es gilt also für alle x ∈∈ ℝ
exp(x) > 0.
Aus f’(x) = f(x) folgt f(x) = c·exp(x), denn mit der Quotientenregel hat man
(f(x)exp(x))’
= f’(x)·exp(x) − exp(x)·f(x)exp2(x) = 0
und hiermit
f(x)exp(x) = konstant.
Mit exp(x) ist auch exp’(x) überall positiv, also ist exp streng monoton wachsend:
x < y ⇒ exp(x) < exp(y).
Wegen dieser Monotonie folgt zusammen mit exp(0) = exp’(0) = 1 für x > 0
exp(x) > 1 + x.
Es gibt also zu jeder positiven reellen Zahl s ein x0, so dass für x ≥ x0
exp(x) ≥ s
gilt. Mit anderen Worten: exp(x) strebt gegen ∞ für x → ∞.
Hieraus folgt, dass für x → −∞ exp(x) gegen 0 strebt.
exp(1) ist gleich dem Grenzwert der Euler’schen Reihe, also gleich der Euler’schen Zahl:
exp(1) = e.

Der natürliche Logarithmus
exp ist streng monoton, also auch injektiv. Demnach besitzt exp eine Umkehrfunktion. Diese heißt natürlicher Logarithmus und wird mit ln bezeichnet.
![]() L3
L3
Die Funktion ln ist auf ganz ℝ+ definiert.
Beweis:
exp ist eine injektive Funktion von ℝ nach ℝ+. Das heißt, zu jeder reellen Zahl x gehört
eineindeutig eine positive reelle Zahl y mit y = exp(x).
exp strebt für x → −∞ gegen 0 und für x → ∞ gegen ∞,
also gibt es zu jedem y ∈∈ ℝ+ zwei
reelle Zahlen x1 und x2 mit
exp(x1) < y < exp(x2).
Nach dem Zwischenwertsatz gibt es also eine reelle Zahl x mit exp(x) = y. Hieraus folgt die Bijektivität von exp und damit auch die behauptete Aussage.
![]() L4
L4
Es gilt für x > 0
ln’(x) = 1x.
Beweis:
Sei x = exp(y). Dann folgt mit U3
ln’(x) = 1exp’(y) = 1exp(y) = 1x.

![]() L5 (Additionstheorem des Logarithmus)
L5 (Additionstheorem des Logarithmus)
Für alle x1,x2 ∈∈ ℝ+ gilt
ln(x1·x2) = ln(x1) + ln(x2).
Beweis:
Sei x1 = exp(y1) und x2 = exp(y2).
Dann folgt mit L2
ln(x1·x2)
= ln(exp(y1)·exp(y2))
= ln(exp(y1 + y2))
= y1 + y2
= ln(x1) + ln(x2).
Wegen exp(0) = 1 und exp(1) = e gilt ln(1) = 0 und ln(e) = 1. Zusammen mit L5 folgt für x > 0 aus ln(1) = 0, dass ln(1x) + ln(x) = 0 und damit hat man für x > 0 die Beziehung
ln(1x) = −ln(x).
![]() L6
L6
Sei die positive reelle Zahl x0 fest, aber beliebig gewählt. Dann gilt für alle x mit |x − x0| < x0
ln(x) = ln(x0) + ∞∑k = 1(−1)k+1k·x0k(x − x0)k.
ln ist also nach T6 eine auf ℝ+ analytische Funktion.
Beweis:
Die Folge (k√k)k=1..∞
konvergiert gegen 1 (Beweis).
Also konvergiert auch die Folge (k√k−1)k=1..∞
gegen 1. Daraus folgt mit dem Satz von Cauchy-Hadamard, dass die Reihe
∞∑k = 1(−1)k+1·hkk
konvergiert, sofern |h| kleiner als 1 ist. Es lässt sich demnach durch
f(h) =def ∞∑k = 1(−1)k+1·hkk
die Funktion f auf dem Intervall (−1, 1) definieren. Wegen P3 und P7 ist f auf (−1, 1) differenzierbar und es gilt
f’(h) = ∞∑k = 0(−1)k·hk = ∞∑k = 0(−h)k.
Mit S7 folgt für alle h mit |h| < 1
f’(h) = 11 + h .
Zusammen mit L4 hat man somit
ddh(ln(1+h) − f(h)) = 0
und hieraus folgt
ln(1+h) − f(h) = c
mit einer gewissen Konstanten c. Wegen ln(1 + 0) = 0 = f(0) folgt sofort c = 0.
Sei nun x0 > 0, aber ansonsten beliebig gewählt. Für x mit |x − x0| < x0 und h = x − x0x0 gilt |h| < 1, so dass sich schließlich
ln(1+h) = ln(xx0) = ∞∑k = 1(−1)k+1k·x0k(x − x0)k
ergibt. Hieraus folgt die Behauptung.
Setzt man x0 = 1, so vereinfacht sich die eben bewiesene Formel. Dann gilt für x mit |x − 1| < 1
ln(x) = ∞∑k = 1(−1)k+1k(x − 1)k
oder für x mit |x| < 1
ln(1 + x) = ∞∑k = 1(−1)k+1kxk.
Der Mathematiker und Astronom Nikolaus Mercator hat diese Reihenentwicklung für den natürlichen Logarithmus entdeckt und 1668 als Erster veröffentlicht. Deshalb nennt man die Reihe
x − 12x2 + 13x3 − 14x4 + 15x5 − 16x6 + −...
üblicherweise Mercator-Reihe.
Die Formel von Mercator ist auch für x = 1 gültig.
Beweis:
Die Reihe ∞∑k = 1(−1)k+1kxk
konvergiert nach dem Leibnizkriterium auch für x = 1,
das heißt, dass die durch
f(x) = ∞∑k = 1(−1)k+1kxk
erklärte Funktion f auf [0, 1] definiert werden kann. ln ist überall auf ℝ+ stetig. Die Gleichung ln(1 + x) = f(x) gilt auch für x = 1, wenn gezeigt werden kann, dass auch f an der Stelle 1 stetig ist.
Bezeichnet man die n-ten Partialsummen von ∞∑k = 1(−1)k+1kxk
mit Sn(x), also
S1(x) = x, S2(x) = x − 12x2, ...,
so gilt für m = 1,2,...
S2m(x) ≤ f(x) ≤ S2m+1(x)
und
|S2m+1(x) − S2m(x)| = x2m+12m+1.
Ist x ∈∈ [0, 1], so folgt
x2m+12m+1 ≤ 12m+1.
Sei nun ε > 0
beliebig vorgegeben. Dann gibt es ein m0, so dass für alle m ≥ m0
12m+1 < ε
gilt. Im Fall, dass m ≥ m0, gilt dann für alle x ∈∈ [0, 1]
|f(x) − S2m+1(x)| < ε
und |f(x) − S2m(x)| < ε.
Die Reihe f(x) konvergiert demnach auf [0, 1] gleichmäßig. Mit G1 folgt die Stetigkeit von f an der Stelle 1, was zu zeigen war.
Hiermit folgt
ln(2) = 1 − 12 + 13 − 14 + 15 − 16 + −...,
eines der Kleinode der Mathematik.
Die Exponentialfunktion zur Basis a
Sei a eine positive reelle Zahl. Dann heißt die durch
expa(x) =def exp(x·ln(a))
definierte Funktion expa Exponentialfunktion zur Basis a.
Es folgt sofort, dass expa(x) nur positive Werte annehmen kann. Weiter rechnet man leicht nach, dass expa(0) = 1, expa(1) = a und exp1(x) = 1, expe(x) = exp(x) sowie expa(−x) = (expa(x))−1 für alle x ∈∈ ℝ. Für alle x1,x2 ∈∈ ℝ gilt außerdem
expa(x1 + x2) = expa(x1)·expa(x2).
Hieraus folgt sofort
expa(x + 1) = a·expa(x).
expa wächst dramatisch: Bei jedem Einerschritt, den man in x-Richtung additiv macht, erhält man den jeweils nächsten Funktionswert durch Multiplikation von expa(x) mit a.
![]() L7
L7
Es seien p und q ganze Zahlen, wobei q von 0 verschieden sein soll. Mit
r = pq
gilt
expa(r) = ar = +q√ap.
Beweis:
Sei a eine beliebige positive reelle Zahl.
Zunächst wird gezeigt, dass expa(n) = an für
alle natürlichen Zahlen n gilt, und zwar mit vollständiger Induktion:
Induktionsanfang:
Es gilt expa(0) = 1 = a0.
Induktionsvoraussetzung:
Angenommen, expa(m) = am sei bereits für ein
m ∈∈ ℕ bewiesen.
Induktionsschluss:
expa(m+1) = a·expa(m) = a·am = am+1.
Seien nun p und q ganze Zahlen, wobei ohne Einschränkung der Allgemeinheit angenommen werden darf, dass q positiv ist. Mit r = pq gilt
(expa(r))q = expa(q·r) = expa(p) = ap.
Hieraus folgt die Behauptung.
expa ist nach Definition stetig auf ganz ℝ. Auf der Grundlage von L7 ist so die folgende Definition möglich und sinnvoll:
Ist a eine positive reelle Zahl und x irgendeine reelle Zahl, dann sei
ax =def expa(x).
Man rechnet leicht nach, dass die bekannten Rechenregeln für Potenzen mit natürlichen Exponenten gleichermaßen auch für Potenzen mit reellen Exponenten gelten.
Statt „exp(x)“ kann nun „ex“ geschrieben werden. Die natürliche Exponentialfunktion wird deswegen auch meist nur kurz „e-Funktion“ genannt. Es gilt aufgrund der Definitionen
ax = e ln(a)·x.
Das folgende Diagramm zeigt die Schaubilder einiger Exponentialfunktionen mit unterschiedlichen Basen. Man sieht deutlich, dass relativ kleine Änderungen der Basis a relativ starke Änderungen der Funktionswerte ax bewirken.
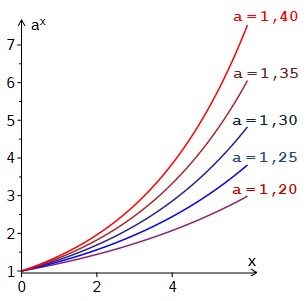
Haben Exponentialfunktionen Basen, die größer als 1 sind, können mit ihnen exponentielle Wachstumsprozesse, haben sie Basen, die kleiner als 1 sind, können mit ihnen exponentielle Zerfallsprozesse beschrieben werden. Im Kapitel Funktion findet sich ein Beispiel hierfür: Der Zerfallsprozess eines radioaktiven Präparates.
Der Logarithmus zur Basis a
Für a > 1 ist ax streng monoton wachsend, für 0 < a < 1 streng monoton fallend. In beiden Fällen wird ℝ durch ax auf ℝ+ also injektiv abgebildet, das heißt, dass für diese ax Umkehrfunktionen existieren. Wie im Beweis von L3 zeigt man auch hier, dass ℝ durch ax auf ℝ+ sogar bijektiv abgebildet wird, so dass die Umkehrfunktionen auf ganz ℝ+ definiert sind.
Sei a eine positive reelle Zahl und verschieden von 1. Dann heißt die auf ℝ+ definierte Umkehrfunktion der Exponentialfunktion zur Basis a Logarithmus zur Basis a und wird mit
loga(x)
bezeichnet.
Der Logarithmus zur Basis 10 (kurz: Zehnerlogarithmus) heißt dekadischer Logarithmus oder Briggscher Logarithmus. Statt „log10“ wird „lg“ (manchmal auch − aber nicht DIN-konform − „log“) geschrieben.
Der Logarithmus zur Basis e ist der natürliche Logarithmus ln.
Mit y = loga(x) folgt x = ay = eln(a)·y und hiernach ln(a)·y = ln(x). Daraus folgt
loga(x) = ln(x)ln(a).
Zusammen mit L5 folgt hieraus
loga(x1·x2) = loga(x1) + loga(x2).
Für x > 0 gilt loga(1) = loga(1x) + loga(x) = 0 und damit hat man
loga(1x) = −loga(x)
und deswegen gilt auch
loga(x1x2) = loga(x1) − loga(x2).
Im Kapitel Verhältnis kann man eine Anwendung dieser Gleichung studieren. Es geht dabei um musikalische Intervalle und wie diese vom menschlichen Ohr wahrgenommen werden.
Die trigonometrischen Funktionen sin und cos
Die Exponentialreihe
∞∑k = 0 xkk!
konvergiert für alle x ∈∈ ℝ. Also
ist nach S2 (xkk!) stets eine
Nullfolge, so dass mit dem Leibnizkriterium
in Verbindung mit F4 folgt, dass die alternierenden Reihen
∞∑k = 0 (−1)kx2k+1(2k+1)!
und
∞∑k = 0 (−1)kx2k(2k)!
auf ganz ℝ konvergent sind.
Demnach sind die folgenden Definitionen möglich:
sin(x) =def ∞∑k = 0 (−1)kx2k+1(2k+1)!
cos(x) =def ∞∑k = 0 (−1)kx2k(2k)!
Die Sinusfunktion sin und die Kosinusfunktion cos sind also nach T6 analytische Funktionen auf ℝ. Aus den Definitionen von sin und cos folgt unmittelbar
sin(−x) = − sin(x)
cos(−x) = cos(x)
und zusammen mit P8
sin’ = cos
cos’ = − sin.
Ferner sieht man sofort, dass sin(0) = 0 und cos(0) = 1 gilt. Damit hat man
cos’(0) = −sin(0) = 0
und cos’’(0) = −cos(0) = −1.
Mit T10 folgt, dass cos an der Stelle 0 ein lokales Maximum besitzt.
![]() L8 (Additionstheoreme für sin und cos)
L8 (Additionstheoreme für sin und cos)
Für alle x1,x2 ∈∈ ℝ
gilt
sin(x1 + x2) = sin(x1)·cos(x2) + cos(x1)·sin(x2)
cos(x1 + x2) = cos(x1)·cos(x2) − sin(x1)·sin(x2).
Beweis:
Sei die reelle Zahl ξ beliebig, aber fest gewählt. Seien ferner die Funktionen f und g durch
f(x) =def sin(x + ξ) − sin(ξ)·cos(x) − cos(ξ)·sin(x)
g(x) =def cos(x + ξ) − cos(ξ)·cos(x) + sin(ξ)·sin(x)
definiert. Man rechnet dann schnell nach, dass f(0) = g(0) = 0 und f’(x) = g(x) bzw. g’(x) = −f(x) gilt.
Sei nun p(x) =def f2(x) + g2(x),
dann folgt unter Anwendung der Kettenregel
p’(x)
= 2·f(x)·f’(x) + 2·g(x)·g’(x)
= 2·f(x)·g(x) − 2·g(x)·f(x)
= 0.
Aus p’(x) = 0 ergibt sich, dass p eine konstante Funktion sein muss. Wegen p(0) = 0 gilt für alle x ∈∈ ℝ p(x) = 0 und damit f2(x) = − g2(x). Hieraus folgt f(x) = g(x) = 0 und damit hat man beide Additionstheoreme.
Ersetzt man im zweiten Additionstheorem x2 durch −x1, so folgt
![]() L9
L9
Für alle x ∈∈ ℝ
gilt
sin2(x) + cos2(x) = 1.
![]() L10
L10
Die Funktion cos hat im Intervall [0, 2] genau eine Nullstelle.
Beweis:
(i) zu zeigen: cos besitzt zwischen 0 und 2 mindestens eine Nullstelle.
Es gilt
cos(x)
=
1 − x22!
+ x44!
− x66!
+ x88! − + ...
=
1 − (x22!
− x44!)
− (x66!
− x88!) − ...
=
1 − x22!
(1
− x23·4)
− x66!
(1
− x27·8) − ...
= 1 −
∞∑k = 0 fk(x) mit
fk(x) = x4k+2(4k+2)!·(1
− x2(4k+3)(4k+4)).
Für 0 < x < 3 sind alle fk(x) positiv (auch f0(x)!), also gilt für diese x
cos(x) < f0(x).
Hieraus folgt cos(2) < − 13. Zusammen mit cos(0) = 1 ergibt sich nach dem Zwischenwertsatz die Existenz einer Nullstelle zwischen 0 und 2.
(ii) zu zeigen: cos besitzt zwischen 0 und 2 höchstens eine Nullstelle.
Es gilt
cos’(x)
=
− sin(x)
=
−x + x33!
− x55!
+ x77!
− x99!
+ x1111! − + ...
=
− (x
− x33!)
− (x55!
− x77!) − ...
=
−x
(1 + x22·3)
− x55!
(1 + x26·7) − ...
=
∞∑k = 0 gk(x) mit
gk(x) = − x4k+1(4k+1)!·(1 + x2(4k+2)(4k+3)).
Für 0 < x ≤ 2 sind alle gk(x) negativ, also gilt für diese x
cos’(x) < 0.
Demnach ist cos im Intervall [0, 2] streng monoton fallend und kann dort somit nur eine einzige Nullstelle haben.
Sei ν die nach L10 einzige Nullstelle von cos im Intervall
[0, 2]. Es wird festgesetzt:
π =def 2·ν.
Nach dieser Definition gilt also
cos(π2)
= 0.
Aus dem Beweis von L10, Teil (ii), folgt, dass
sin(π2) > 0
gilt. Also hat man wegen
sin2(π2)
+ cos2(π2)
= sin2(π2)
+ 0 = 1
sin(π2)
= 1.
Aus den Additionstheoremen für sin und cos ergeben sich unmittelbar die Formeln
sin(2x) = 2·sin(x)·cos(x),
cos(2x) = cos2(x) − sin2(x).
Hiermit hat man
sin(π) =
2 sin(π2)
cos(π2)
= 0,
cos(π) =
cos2(π2)
− sin2(π2)
= −1.
![]() L11
L11
sin und cos sind periodische Funktionen. Die Periode beider Funktionen ist gleich 2π,
das heißt für alle
x ∈∈ ℝ
gilt
sin(x + 2π) = sin(x),
cos(x + 2π) = cos(x)
und aus sin(x + h) = sin(x)
bzw.
cos(x + h) = cos(x)
folgt h = k·2π
mit k ∈∈ ℤ.
Beweis:
Wegen cos(π2)
= 0
und sin(π2)
= 1 ergeben sich aus den Additionstheoremen für sin und cos die folgenden zwei Formeln:
sin(x + π2) = cos(x),
cos(x + π2) = − sin(x).
Hieraus folgt
sin(x + π) = sin((x + π2) + π2) = − sin(x),
cos(x + π) = cos((x + π2) + π2) = − cos(x)
und schließlich
sin(x + 2π) = sin((x + π) + π) = sin(x),
cos(x + 2π) = cos((x + π) + π) = cos(x).
Sei nun angenommen, dass für alle
x ∈∈ ℝ
sin(x + h) = sin(x) gilt mit
0 < h < 2π.
Dann folgt mit dem Additionstheorem für sin, dass sin(h) = 0 gelten muss.
Wegen sin(π2 + x) = cos(x)
sind die Schaubilder von sin und cos um
π2
in x-Richtung gegeneinander verschoben, aber von der Form her identisch.
π2
ist die einzige Nullstelle von cos zwischen 0 und π, also ist demzufolge π
die einzige Nullstelle von sin zwischen π2
und 3·π2.
Es folgt also h = π. π ist jedoch keine Periode,
denn es ist sin(3·π2) = cos(π) = −1,
aber sin(π2)
= 1. Damit folgen für sin und ebenso für cos die behaupteten Aussagen.
![]() L12
L12
Für alle
x ∈∈ ℝ
gilt
sin(π − x) = sin(x),
cos(π − x) = − cos(x).
Beweis:
Beide Formeln folgen sofort aus sin(x + π) = − sin(x) bzw.
cos(x + π) = − cos(x) unter
Beachtung von sin(x) = − sin(−x)
und cos(x) = cos(−x).
Aus Symmetriegründen ergibt sich unmittelbar die Beziehung
sin(π4) = cos(π4).
Ein Beispiel für die Anwendung der Kosinusfunktion: Schwingt ein schwerer Gegenstand in einem zähen Medium, so wird die Schwingung durch Reibung gedämpft. Unter der Annahme, dass sich diese Reibung proportional zur Geschwindigkeit des schwingenden Körpers verhält und die Reibung nicht zu groß ist, lässt sich der Schwingungsvorgang durch eine Gleichung der folgenden Art beschreiben (siehe Maple-Worksheet Schwingungen):
x(t) = x0·e−kt·cos(ωt).
x(t) ist hierbei die Auslenkung des schwingenden Körpers relativ zu seiner Ruheposition in Abhängigkeit von der
Zeit t. x0 ist die Position des Körpers zur Zeit t = 0.
Mit x0 = 1, k = 0,2 und
ω = 2 ergibt sich folgendes Schaubild:
Die Kreiszahl π
Die Definition von π als dem Zweifachen der kleinsten positiven Nullstelle von cos
ist − wenn man sie zum ersten Mal liest − möglicherweise etwas irritierend, kennt man doch
die Kreiszahl π normalerweise als Konstante, die das Verhältnis des Umfangs eines beliebig
großen Kreises zu seinem Durchmesser angibt. Mit dem folgenden Satz wird eine Verbindung zwischen diesen zwei
Aspekten der Kreiszahl hergestellt. Zum Beweis von L13 werden allerdings Rechengesetze der Integralrechnung benötigt:
![]() L13
L13
Für den Flächeninhalt A eines Kreises mit dem Radius 1 gilt
A = π.
Für den Flächeninhalt A* eines Halbkreises mit dem Radius 1 gilt
A* = 1∫−1√1 − x2dx.
Substitution von x durch −cos(t) liefert unter Beachtung von −cos(0) = −1 und
−cos(π) = 1
A* = π∫0√1 − cos2(t)sin(t)dt
und damit
A* = π∫0sin2(t)dt.
Mit der Regel der partiellen Integration folgt wegen sin(π) = sin(0) = 0
π∫0sin2(t)dt = π∫0cos2(t)dt
und somit hat man mit 1 = sin2(t) + cos2(t)
π = π∫01 dt = 2π∫0sin2(t)dt.
Es folgt A* = π2, was zu zeigen war.
![]() L14
L14
Der Umfang eines Kreises mit dem Radius 1 ist gleich 2π.
Beweis:
Der Umfang U eines Kreises ist zu seinem Durchmesser d proportional
(→ Beweis). Es gibt also eine konstante Zahl p, so dass
U = p·d. Außerdem gilt für den Flächeninhalt A eines Kreises mit dem Durchmesser d
A = U2·d2.
Mit L13 folgt nach kurzer Rechnung p = π
und damit die Behauptung.
Um die eben benutzte Formel für den Kreisflächeninhalt A zu verstehen, zerlege man eine Kreisfläche in n flächengleiche Sektoren (wobei n eine gerade Zahl sein muss) und setze diese wie nachstehend abgebildet wieder in einer Figur Fn zusammen.
Die Grenzfigur der Figurenfolge (Fn)n=2..∞ ist ein Rechteck mit der Länge U2 und der Höhe d2.
Aus dem Vorangegangenen folgt ohne Weiteres
![]() L15
L15
Der Umfang eines Kreises mit dem Radius r ist gleich 2πr.
Der Flächeninhalt eines Kreises mit dem Radius r ist gleich πr2.
sin(x) und cos(x) geometrisch gedeutet
Mit dem Satz des Pythagoras, wonach in einem rechtwinkligen Dreieck die Summe beider Kathetenquadrate gleich dem
Hypotenusenquadrat ist, erhält man wegen L9 unter Beachtung von
sin(0) = 0 und cos(π2) = 0
sowie X76 eine geometrische Deutung der trigonometrischen Ausdrücke sin(x) und cos(x):
![]() L16
L16
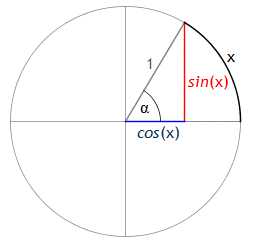
Hierbei ist x gleich der Länge des zum Winkel α gehörenden Kreisbogens mit dem Radius 1.
Entgegen des Uhrzeigersinns (so wie in der Zeichnung zu sehen) wird x positiv, im Uhrzeigersinn negativ gerechnet.
x ist das Bogenmaß des Winkels α. Man schreibt
x = arc(α).
arc ist die Abkürzung von arcus (lateinisch: der Bogen).
Die trigonometrischen Funktionen tan und cot
Neben der Sinus- und der Kosinusfunktion gibt es noch die trigonometrischen Funktionen Tangens und Kotangens:
tan(x) =def sin(x)cos(x)
mit x ǂ (k + 12) π, k ∈∈ ℤ;
cot(x) =def cos(x)sin(x)
mit x ǂ kπ, k ∈∈ ℤ.
Die Anwendung der Quotientenregel liefert
tan’(x) = 1cos2(x) = 1 + tan2(x),
cot’(x) = − 1sin2(x) = − (1 + cot2(x)).
Auch die Ausdrücke tan(x) und cot(x) lassen sich geometrisch deuten. Unter Verwendung der Strahlensätze ergibt sich das folgende Diagramm:
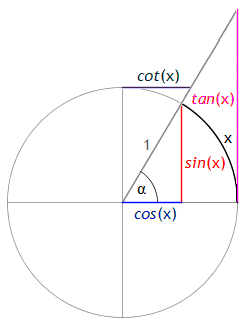
Arkusfunktionen
Schränkt man die jeweiligen Definitionsbereiche der trigonometrischen Funktionen auf folgende Intervalle ein:
Dsin = [−π2, π2],
Dcos = [0, π],
Dtan = (−π2, π2)
sowie Dcot = (0, π),
so sind die Funktionen sin: Dsin → [−1, 1],
cos: Dcos → [−1, 1],
tan: Dtan → ℝ und
cot: Dcot → ℝ
allesamt bijektiv und damit umkehrbar. Die Umkehrfunktionen dieser Funktionen heißen Arkusfunktionen (oder
zyklometrische Funktionen) und werden mit arcsin, arccos, arctan bzw. arccot,
manchmal auch mit sin−1, cos−1, tan−1 bzw. mit cot−1
bezeichnet.

Es gilt arccos(x) = π2 − arcsin(x)
bzw. arcsin(x) = π2 − arccos(x).
Für x ∈∈ (−1, 1) gilt sin’(x) ǂ 0. Deswegen ist nach U3 arcsin auf (−1, 1) differenzierbar und es gilt
arcsin’(x) = 1sin’(y) = 1cos(y) = 1+√1 − sin2(y) = 1+√1 − x2.
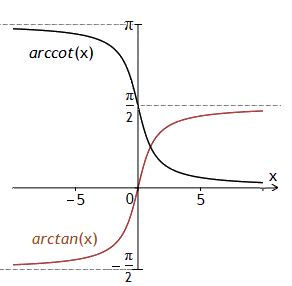
Es gilt arctan(x) = π2 − arccot(x)
bzw. arccot(x) = π2 − arctan(x).
tan’(x) ist nirgendwo gleich 0; es gilt
arctan’(x) = 1tan’(y) = 11 + tan2(y) = 11 + x2.
![]() L17
L17
Für alle x ∈∈ (−1, 1]
gilt
arctan(x) = ∞∑k = 0 (−1)kx2k+12k+1.
Beweis:
Mit dem Leibnizkriterium folgt, dass die alternierende Reihe
∞∑k = 0 (−1)kx2k+12k+1
für |x| < 1 konvergiert. Für diese x ist also die Funktion f, erklärt durch
f(x) =def ∞∑k = 0 (−1)kx2k+12k+1,
wohldefiniert. Wegen P3 und P8 darf man f(x) gliedweise differenzieren. Somit gilt
f’(x) = ∞∑k = 0 (−1)kx2k.
Die Reihe ∞∑k = 0 (−1)kx2k ist auch konvergent für |x| < 1 und es gilt
unter Beachtung von S1
f’(x) + f’(x)·x2 = 1.
Demzufolge ist sowohl f’(x) als auch arctan’(x) gleich 11 + x2, also hat man
f’(x) − arctan’(x) = 0.
Hieraus folgt, dass f(x) − arctan(x) konstant sein muss. Wegen f(0) = arctan(0) ist damit für |x| < 1 die behauptete Aussage arctan(x) = f(x) bewiesen.
Die Reihe f(x) konvergiert nach dem Leibnizkriterium auch für x = 1. arctan ist überall auf ℝ stetig. Die Gleichung arctan(x) = f(x) gilt auch für x = 1, wenn gezeigt werden kann, dass auch f an der Stelle 1 stetig ist.
Bezeichnet man die n-ten Partialsummen von ∞∑k = 0 (−1)kx2k+12k+1
mit Sn(x), so gilt für m = 1,2,...
S2m−1(x) ≤ f(x) ≤ S2m(x)
und
|S2m(x) − S2m−1(x)| = x4m+14m+1.
Ist x ∈∈ [0, 1], so folgt
x4m+14m+1 ≤ 14m+1.
Sei nun ε > 0
beliebig vorgegeben. Dann gibt es ein m0, so dass für alle m ≥ m0
14m+1 < ε
gilt. Im Fall, dass m ≥ m0, gilt dann für alle x ∈∈ [0, 1]
|f(x) − S2m−1(x)| < ε
und |f(x) − S2m(x)| < ε.
Die Reihe f(x) konvergiert demnach auf [0, 1] gleichmäßig. Mit G1 folgt die Stetigkeit von f an der Stelle 1, was zu zeigen war.
Wegen sin(π4) = cos(π4) gilt
tan(π4) = 1
und mit L17 folgt die Formel, welche zu Beginn dieses Kapitels bereits vorgestellt wurde:
π4 = 1 − 13
+ 15
− 17
+ 19
− 111 + −...
Literatur- und Quellenangaben:
Richard Courant:
Vorlesungen über Differential- und Integralrechnung Band 1
Springer-Verlag, 4. Auflage 1971
Hans Grauert/Ingo Lieb:
Differential- und Integralrechnung I
Springer-Verlag, 2. Auflage 1970
Oliver Deiser:
Analysis I
www.aleph1.info 2021

