Vollständige Induktion
Die Axiome von Giuseppe Peano (1858−1932), welche die grundlegenden Eigenschaften der Menge der natürlichen Zahlen beschreiben, lauten − umgangssprachlich formuliert − etwa so:
(1) 0 ist eine natürliche Zahl.
(2) Jede natürliche Zahl hat einen Nachfolger und dieser ist
wieder eine natürliche Zahl.
(3) Enthält eine Menge S die Zahl 0 und mit jeder natürlichen Zahl
auch stets deren Nachfolger, so enthält S alle natürlichen Zahlen.
(4) Sind die Nachfolger zweier natürlicher Zahlen a und b
einander gleich, so sind auch a und b einander gleich.
(5) Kein Nachfolger einer natürlichen Zahl ist gleich der Zahl 0.
Diese Axiome sind nicht unproblematisch, denn die Begriffe „Zahl“, „0“ und „Nachfolger“ werden in (1) bis (5) im mathematischen Sinne nicht definiert. Es gibt zum Axiomensystem von Peano folgende äquivalente Alternative unter Benutzung des Begriffs der Abbildung:
(I) ℕ ist eine nichtleere Menge.
(II) Es gibt eine injektive Abbildung succ: ℕ → ℕ.
(III) Genau ein Element in ℕ hat kein Urbild unter succ.
Dieses Element soll „0“ heißen.
(IV) Sei M eine Teilmenge von ℕ mit den folgenden
zwei Eigenschaften:
(i) 0 ∈∈ M
(ii) m ∈∈ M ⇒ succ(m) ∈∈ M.
Dann folgt: M = ℕ.
Mit dieser Beschreibung von ℕ handelt man sich ein anderes Problem ein: Die Axiome (II) und (III) zur Definition der Abbildung succ auf der Menge ℕ setzt die Existenz von ℕ bereits voraus, obwohl ja erst mit Hilfe des Axiomensystems (I) bis (IV) die Menge ℕ definiert werden soll.
Man kann es drehen und wenden wie man will, im Grunde wird gefordert, dass ℕ eine wohlgeordnete und unendliche Menge ist mit 0 ∈∈ ℕ als kleinstem Element, und mit den Axiomen (I) bis (IV) ist sichergestellt, dass mit ihnen die Wohlgeordnetheit von ℕ bewiesen werden kann. Das Aufeinanderfolgen der wohlgeordneten natürlichen Zahlen ist das mathematische Pendant zu dem elementaren Tun des Hintereinanderreihens von wohlunterschiedenen Objekten, das heißt dem Prozess des Zählens.
Die Aussage „ℕ ist eine wohlgeordnete Menge“ muss - wenn man den Ausdruck „wohlgeordnet“ noch nicht kennt - näher erläutert werden:
Sei M eine nichtleere Menge gleichartiger Objekte und
R ⊂ M x M = { (x;y): x∈∈M und y∈∈M }
eine Relation auf M. Dann heißt (M, R) genau dann (reflexive) Halbordnung, wenn für alle x,y,z ∈∈ M Folgendes gilt:
x R y und
y R z ⇒ x R z
(Transitivität)
x R y und
y R x ⇒ x = y
(Identitivität)
x R x (Reflexivität)
Ist (M, R) eine Halbordnung, so sagt man: „M ist partiell geordnet“. Ist (M, R) eine reflexive Halbordnung und gilt außerdem noch für alle x,y ∈∈ M
x R y oder y R x (Konnexität)
dann heißt M linear geordnet (oder total geordnet).
Aus einer reflexiven Halbordnung (M, R) erhält man mit der Definition
x r y ⇔def x R y und x ǂ y
die irreflexive Halbordnung (M, r). Für diese irreflexive Halbordnung gelten die folgenden zwei Regeln:
x r y und
y r z ⇒ x r z
(Transitivität)
Es gibt kein x ∈∈ M mit
x r x (Irreflexivität).
Für eine Menge M, die irreflexiv und linear geordnet ist, gilt darüberhinaus für alle x,y ∈∈ M
x r y oder y = x oder y r x (Konnexität).
Aus einer irreflexiven Halbordnung (M, r) erhält man mit der Definition
x R y ⇔def x r y oder x = y
die reflexive Halbordnung (M, R).
Eine wohlgeordnete Menge ist eine linear geordnete Menge M, in der jede nichtleere Teilmenge T ein kleinstes Element xmin besitzt, das heißt für jede Teilmenge T ⊂ M muss gelten:
∃ xmin ∈∈ T: xmin R x für alle x ∈∈ T.
Die Menge der natürlichen Zahlen ist mit der Relation ≤ wohlgeordnet.
Für die Herleitung der Gesetze in ℕ nur unter Verwendung der Axiome (I) bis (IV) formuliert man zweckmässigerweise das sogenannte Prinzip der vollständigen Induktion:
Das Prinzip der vollständigen Induktion
![]()
Sei mit „E(n)“ irgendeine Aussage bezeichnet, die in
Abhängigkeit von n ∈∈ ℕ
formuliert werden kann. Wenn „ℰ(n)“
die Abkürzung für „Die Aussage E(n) ist wahr“ bedeutet, dann lautet
das Prinzip der vollständigen Induktion wie folgt:
Gilt für m ∈∈ ℕ
(i) ℰ(0)
und
(ii) ℰ(m) ⇒ ℰ(succ(m)),
so folgt: ℰ(n) für alle n ∈∈ ℕ.
(i) heißt Induktionsanfang und (ii) heißt Induktionsschluss.
„ℰ(m)“
heißt
Induktionsvoraussetzung (oder Induktionsannahme).
Das Prinzip der vollständigen Induktion ergibt sich unmittelbar aus dem Axiom (IV):
Beweis:
Sei M =def {m ∈∈ ℕ
| ℰ(m) }. M ist damit eine Teilmenge
von ℕ und enthält alle diejenigen natürlichen
Zahlen, für welche ℰ(m) gilt:
ℰ(m) ⇔ m ∈∈ M
für alle m ∈∈ ℕ.
Die Aussage ℰ(m) ⇒ ℰ(succ(m))
ist also äquivalent zu m ∈∈ M ⇒ succ(m) ∈∈ M.
Wenn nun gemäß (ii) für jedes beliebig gewählte Element m von M folgt,
dass immer auch succ(m) ein Element von M ist und gemäß (i) 0 ∈∈ M
gilt (was äquivalent ist zu ℰ(0)),
dann folgt mit Axiom (IV),
dass M = ℕ
. Die Aussage „M = ℕ“
wiederum ist nach Definition von M äquivalent zu „ℰ(n) für alle n ∈∈ ℕ“.
Oftmals führt man einen Induktionsbeweis nur über einer (natürlich nach oben nicht beschränkten) Teilmenge von ℕ aus. Dann kann man auf Grundlage des Induktionsprinzips wie folgt argumentieren:
Wenn für irgendeine Aussage E, die in Abhängigkeit von n ∈∈ ℕ
mit n ≥ k
formuliert werden kann, für m ≥ k gilt:
(i) ℰ(k)
und
(ii) ℰ(m) ⇒
ℰ(succ(m)),
so folgt: ℰ(n) für alle n ≥ k.
Richard Dedekind (1831−1916)
hat in seiner Schrift Was sind und was sollen Zahlen? 1887 das Induktionsprinzip nicht als Axiom, sondern als
beweisbaren Satz präsentiert. Dies liegt daran, dass Dedekind auf (nach
heutigem Sprachgebrauch) mengentheoretischem Wege zu einer Charakterisierung
der natürlichen Zahlen gelangt und dann hieraus den Satz der
vollständigen Induktion ableitet. Der wesentliche Begriff hierbei ist
der der „Kette“. Im Folgenden soll die Dedekind'sche Argumentation in
heutiger Terminologie (→ Definitionen) vorgestellt werden.
Sei S eine nichtleere Menge und φ: S → S eine injektive Abbildung, das heißt es gilt a ǂ b ⇒ φ(a) ǂ φ(b) für alle a,b ∈∈ S.
Ist K eine nichtleere Teilmenge von S, dann heißt K eine φ-Kette (oder kurz Kette), wenn φ(K) ⊆ K ist.
Sei A irgendeine nichtleere Teilmenge von S. Dann heißt die Schnittmenge all derjenigen φ-Ketten K, für welche A ⊆ K gilt, die Kette von A. Die Kette von A soll mit KA bezeichnet werden. Besteht die Menge A nur aus einem einzigen Element a, so soll Ka geschrieben werden.
Da S nach Definition eine Kette ist, ist KA nie leer. KA ist die Schnittmenge von φ-Ketten, also ist KA ebenfalls eine φ-Kette. Damit ist die Bezeichnung „Kette von A“ für KA gerechtfertigt.
Mit den eben verwendeten Bezeichnungen folgt unmittelbar
| (K1) | A ⊆ KA |
| (K2) | φ(KA) ⊆ KA |
| (K3) | A ⊆ K ⇒ KA ⊆ K. |
A und B seien nichtleere Teilmengen von S, φ: S → S sei eine injektive Abbildung und es gelte A ⊆ B. Dann gilt auch φ(A) ⊆ φ(B) und mit (K1) folgt φ(A) ⊆ φ(KA). Wegen (K2) hat man dann φ(A) ⊆ KA.
Sei M eine nichtleere Teilmenge von S. Dann gilt
M ⊆ KA ⇔ KM ⊆ KA.
Beweis:
„⇒“:
Aus M ⊆ KA
folgt unter Verwendung von (K3): KM ⊆ KA,
denn KA ist eine Kette.
„⇐“:
Zusammen mit M ⊆ KM
folgt aus KM ⊆ KA:
M ⊆ KA.
Es gilt ferner
M ⊆ KA ⇒ φ(M) ⊆ KA.
Beweis:
Aus M ⊆ KA
folgt aus dem vorherigen Satz KM ⊆ KA.
Zusammen mit φ(M) ⊆ KM
(wegen K2) folgt die Behauptung.
Der Dedekind’sche Satz der vollständigen Induktion lautet nun wie folgt:
Sei A irgendeine nichtleere Teilmenge einer Menge S
und
φ: S → S eine injektive Abbildung.
Sei P irgendeine weitere Menge.
Wenn gezeigt werden kann, dass
| (1) | A ⊂ P |
| (2) | φ(s) ∈∈ P für
alle s ∈∈ KA∩P, |
dann gilt KA ⊆ P.
Beweis:
Die Schnittmenge KA∩P wird im Folgenden mit G bezeichnet.
Es ist A ⊆ KA und wegen (K1) A ⊂ P folgt A ⊆ G. G ist also eine nichtleere Menge.
G ⊆ KA und
KA ⊆
S (wegen K3). Also folgt G ⊆ S.
Ferner folgt aus G ⊆ KA wegen des zuletzt bewiesenen Satzes: φ(G) ⊆ KA.
Aufgrund der Bedingung (2) gilt φ(G) ⊆ P.
Zusammen mit φ(G) ⊆ KA folgt somit: φ(G) ⊆ G, also ist G eine
Kette.
Aus A ⊆ G folgt hieraus wegen (K3) KA ⊆ G.
Es gilt also gleichzeitig G ⊆ KA
und KA ⊆ G. Also
ist KA = KA ∩ P.
Hieraus folgt die Behauptung.
Wenn man P interpretiert als Menge von Objekten, die allesamt eine bestimmte Eigenschaft E besitzen und zeigen kann, dass (1) alle Elemente aus A diese Eigenschaft besitzen und (2) das Bild φ(s) jedes Elements s ∈∈ KA, das diese Eigenschaft besitzt, diese Eigenschaft ebenfalls hat, dann folgt mit dem Induktionssatz, dass alle Elemente der Kette KA die Eigenschaft E haben.
Eine Menge N mit dem Grundelement e heißt abzählbar unendlich, wenn folgende Bedingungen erfüllt sind:
(a) Es gibt eine Abbildung φ: N → N mit φ(N) ⊆ N.
(b) N = Ke.
(c) e ist nicht in φ(N) enthalten.
(d) Die Abbildung φ ist injektiv.
φ(n) mit n ∈∈ N wird das auf n folgende Element genannt.
Dies ist im Wesentlichen die Dedekind'sche Charakterisierung einer abzählbar unendlichen Menge (von ihm damals einfach unendliche Menge genannt) und er sagt: „Wenn man bei der Betrachtung eines einfach unendlichen, durch eine Abbildung φ geordneten Systems N von der besonderen Beschaffenheit der Elemente gänzlich absieht, lediglich ihre Unterscheidbarkeit festhält und nur die Beziehungen auffasst, in die sie durch die ordnende Abbildung φ zueinander gesetzt sind, so heißen diese Elemente natürliche Zahlen oder Ordinalzahlen...“ (R. Dedekind: Was sind und was sollen Zahlen?, Braunschweig 19113, S. 17).
Für jede natürliche Zahl n gilt
Kn = { n } ∪ φ(Kn).
Beweis:
Sei n irgendeine natürliche Zahl und φ(n) Teil einer φ-Kette
L.
Setzt man K = {n} ∪ L, so ist φ(K) = {φ(n)} ∪ φ(L).
φ(L) ⊆ L, weil L eine Kette ist, {φ(n)} ⊆ L nach Voraussetzung, also folgt φ(K) ⊆ L.
Da L ⊆ K folgt φ(K) ⊆
K und damit ist bewiesen, dass K = {n} ∪ L eine
Kette ist.
Nun soll gezeigt werden, dass das Bild der Kette von n gleich der Kette des Bildes von n ist, das heißt:
φ(Kn) = Kφ(n).
Kφ(n) ist eine φ-Kette, also gilt (wegen
K1) φ(n) ∈∈ Kφ(n).
Nach dem Vorhergehenden gibt es dann eine Kette K mit n ∈∈ K und φ(K) ⊆ Kφ(n).
Mit (K3) folgt Kn ⊆ K
und hiermit gilt auch φ(Kn) ⊆ φ(K).
Aus φ(Kn) ⊆ φ(K)
und φ(K) ⊆ Kφ(n)
folgt φ(Kn) ⊆ Kφ(n).
Andererseits ist wegen (K1) n ∈∈ Kn und damit auch φ(n) ∈∈ φ(Kn).
φ(Kn) ist als Bild der Kette Kn
wieder eine Kette. Also folgt mit (K3): Kφ(n) ⊆ φ(Kn).
Aus φ(Kn) ⊆ Kφ(n) und Kφ(n) ⊆ φ(Kn) folgt φ(Kn) = Kφ(n).
Sei nun K = {n} ∪ φ(Kn).
Weil φ(Kn) eine Kette ist, ist auch K eine
Kette (siehe oben).
Nach Definition ist n ∈∈ K, also folgt mit (K3) Kn ⊆ K.
Nach (K1) ist n ∈∈ Kn und nach (K2) Kφ(n) = φ(Kn) ⊆ Kn.
Aus {n} ⊆ Kn und φ(Kn) ⊆ Kn
folgt K ⊆ Kn.
Aus Kn ⊆ K und K ⊆ Kn folgt die Behauptung.
Es folgt unmittelbar
N = { e } ∪ φ(N).
Dies bedeutet, dass jede von der Grundzahl e verschiedene Zahl Element von φ(N) ist, das heißt, jede natürliche Zahl n mit n ǂ e ist das Bild einer anderen natürlichen Zahl. Insbesondere ist die auf e folgende Zahl auch Element von φ(N).
Wenn mit der abzählbar unendlichen Menge N die Menge der natürlichen Zahlen gemeint ist, soll nun statt „N“ „ℕ“ und statt „e“ „0“ geschrieben werden. (Dedekind nennt das Grundelement der natürlichen Zahlen „1“, aber das ist im Hinblick auf die hier vorgestellten Gedankengänge ohne Belang.)
Sei nun E(n) eine Aussage, die in Abhängigkeit von n ∈∈ ℕ hingeschrieben werden kann und sei ferner P diejenige Menge von Zahlen z, für die E(z) eine wahre Aussage darstellt. (Die Verwendung der Bezeichnung „z“ soll hier keine Verwirrung stiften, sondern nur andeuten, dass E(z) durchaus wahr sein kann, wenn z keine natürliche Zahl ist.) Wenn nun der Dedekind'sche Induktionssatz auf die natürlichen Zahlen angewendet und A durch { 0 }, S durch ℕ und φ durch succ ersetzt wird, dann erhält man genau das oben bereits formulierte Prinzip der vollständigen Induktion.
Es sollen jetzt alle Gesetze, die innerhalb der Menge der natürlichen Zahlen gelten, auf Grundlage des Axiomensystems (I) bis (IV) hergeleitet werden.
Addieren und Multiplizieren natürlicher Zahlen
![]()
Die Abbildung addk: ℕ → ℕ sei auf induktive Weise für jedes k ∈∈ ℕ wie folgt definiert:
(A1) addk(0) =def
k
(A2) addk(succ(n)) =def succ(addk(n))
für alle n ∈∈ ℕ
![]() V1
V1
Für alle k, n ∈∈ ℕ gilt
succ(addk(n)) = addsucc(k)(n).
Beweis:
Sei k ∈∈ ℕ beliebig, aber fest gewählt.
Induktionsanfang:
Mit (A1) folgt succ(addk(0)) = succ(k) =
addsucc(k)(0).
Das bedeutet, dass die behauptete Aussage für n = 0 wahr ist.
Induktionsvoraussetzung:
Es gelte
succ(addk(m)) = addsucc(k)(m)
für ein m ∈∈ ℕ.
Induktionsschluss:
succ(addk(succ(m)))
=
succ(succ(addk(m))) wegen (A2)
=
succ(addsucc(k)(m)) nach
Induktionsvoraussetzung
= addsucc(k)(succ(m)) wegen (A2)
Hieraus folgt die Behauptung.
![]() V2
V2
Für alle k,n ∈∈ ℕ
gilt
addk(n) = addn(k).
Beweis:
Zunächst wird gezeigt, dass für alle n ∈∈ ℕ die
Aussage add0(n) = n wahr ist.
Induktionsanfang:
Nach (A1) gilt add0(0) = 0.
Induktionsvoraussetzung:
Angenommen, die Aussage add0(m) = m sei bereits für ein m ∈∈ ℕ bewiesen.
Induktionsschluss:
add0(succ(m))
= succ(add0(m)) wegen (A2)
= succ(m) nach Induktionsvoraussetzung.
Es ist nun zu zeigen, dass die Aussage addk(n) = addn(k) wahr ist für alle n,k ∈∈ ℕ.
Sei k im Folgenden eine beliebige, aber fest gewählte natürliche Zahl.
Induktionsanfang:
addk(0)
= k wegen (A1)
= add0(k) weil add0(n) = n
für alle n ∈∈ ℕ.
Induktionsvoraussetzung:
Es gelte bereits addk(m) = addm(k) für
ein m ∈∈ ℕ.
Induktionsschluss:
addk(succ(m))
= succ(addk(m)) wegen (A2)
= succ(addm(k)) nach Induktionsvoraussetzung
= addsucc(m)(k) wegen V1.
Da hiernach die Aussage addk(n) = addn(k) für alle n ∈∈ ℕ und für jedes beliebige k ∈∈ ℕ wahr ist, ist damit die Behauptung bewiesen.
Die Abbildung mulk: ℕ → ℕ sei für jedes k ∈∈ ℕ wie folgt definiert:
(M1) mulk(0) =def 0
(M2) mulk(succ(n)) =def addk(mulk(n))
für alle n ∈∈ ℕ.
![]() V3
V3
Für alle k,n ∈∈ ℕ
gilt
mulk(n) = muln(k).
Beweis:
(i) Als erstes wird gezeigt, dass addk(mulm(k)) = mulsucc(m)(k)
für alle m,k ∈∈ ℕ.
Sei hierfür m ∈∈ ℕ beliebig, aber fest gewählt.
Induktionsanfang:
add0(mulm(0)) =
add0(0) = 0 = mulsucc(m)(0)
Induktionsvoraussetzung:
Es gelte addK(mulm(K)) = mulsucc(m)(K)
für ein K ∈∈ ℕ.
Induktionsschluss:
addsucc(K)(mulm(succ(K)))
= addsucc(K)(addm(mulm(K)))
wegen (M2)
= succ(addK(addm(mulm(K)))) wegen V1
= succ(addm(addK(mulm(K)))) wegen V2
= addsucc(m)(addK(mulm(K))) wegen V1
= addsucc(m)(mulsucc(m)(K))
nach Induktionsvoraussetzung
= mulsucc(m)(succ(K)) wegen (M2)
(ii) Im zweiten Schritt wird gezeigt, dass für alle n ∈∈ ℕ die
Aussage mul0(n) = 0 wahr ist.
Induktionsanfang:
Nach (M1) gilt mul0(0) = 0.
Induktionsvoraussetzung:
Angenommen, die Aussage mul0(m) = 0 sei
bereits für ein m ∈∈ ℕ bewiesen.
Induktionsschluss:
mul0(succ(m))
= add0(mul0(m)) wegen (M2)
= add0(0) nach Induktionsvoraussetzung
= 0
(iii) Es ist nun zu zeigen, dass die Aussage mulk(n) = muln(k)
wahr ist für alle n,k ∈∈ ℕ.
Sei k im Folgenden eine beliebige, aber fest gewählte natürliche Zahl.
Induktionsanfang:
mulk(0)
= 0 wegen (M1)
= mul0(k)
Induktionsvoraussetzung:
Es gelte bereits mulk(m) = mulm(k) für
ein m ∈∈ ℕ.
Induktionsschluss:
mulk(succ(m))
= addk(mulk(m)) wegen (M2)
= addk(mulm(k)) nach Induktionsvoraussetzung
= mulsucc(m)(k) aufgrund der unter (i)
bewiesenen Regel.
Da hiernach die Aussage mulk(n) = muln(k) für alle n ∈∈ ℕ und für jedes beliebige k ∈∈ ℕ wahr ist, ist damit die Behauptung bewiesen.
Nun werden die Addition und die Multiplikation als zweistellige Operationen auf
ℕ definiert:
Eine 2-stellige Operation (oder eine Verknüpfung) auf einer Menge M ist eine Abbildung
@: M x M → M ,
das heißt, jedem geordneten Paar (x; y) mit x ∈∈ M und y ∈∈ M wird durch eine Zuordnungsvorschrift in eindeutiger Weise ein Bild @(x; y) ∈∈ M zugeordnet.
Sei auf einer Menge M eine Verknüpfung @ definiert und seien x,y ∈∈ M und z ∈∈ M das Bild von (x; y) ∈∈ M2 unter @. Dann sind folgende Schreibweisen gleichbedeutend:
@((x; y)) = z
@(x; y) = z
@(x, y) = z
x @ y = z
Die Verknüpfungen „+“ (Addition) und „·“ (Multiplikation) werden auf ℕ für alle k,n ∈∈ ℕ wie folgt definiert:
k + n =def addk(n)
k · n =def mulk(n)
Die Multiplikation hat gegenüber der Addition die höhere Prioriät, das heißt, für alle k,m,n ∈∈ ℕ gilt:
k + m · n =def k
+ (m · n)
k · m + n =def (k · m) + n
Anschaulich gesprochen: „Punktrechnung geht vor Strichrechnung“.
Wegen addk(n) = addn(k) bzw. mulk(n) = muln(k) für alle k,n ∈∈ ℕ sind die Verknüpfungen „+“ und „·“ kommutativ, das heißt, für alle k,n ∈∈ ℕ gilt:
k + n = n + k
k · n = n
· k
![]() V4
V4
Es gelten für alle k,n ∈∈ ℕ
folgende Rechenregeln:
n + 0 = n
k + succ(n) = succ(k + n)
n · 0 = 0
k · succ(n) = k + (k·n)
Beweis:
Unter Beachtung von k + n = addk(n)
und k·n = mulk(n)
folgt
n + 0 = n unmittelbar aus (A1),
k + succ(n) = succ(k + n)
aus (A2),
n · 0 = 0
aus (M1) und
k · succ(n) = k + (k·n)
aus (M2).
![]() V5
V5
Die Verknüpfungen „+“ und „·“ sind assoziativ, das heißt, für alle k,m,n ∈∈ ℕ gilt
m + (n + k) = (m + n) + k
m · (n · k) = (m
· n) · k
und es gilt das Distributivgesetz
k · (m + n) = k · m + k · n.
Beweis:
Assoziativgesetz bezüglich der Addition.
Induktionsanfang:
m + (n + 0) = m + n = (m + n) + 0
Das bedeutet, dass die behauptete Aussage für k = 0 wahr ist.
Induktionsvoraussetzung:
Es gelte m + (n + K) = (m + n) + K für ein K ∈∈ ℕ.
Induktionsschluss:
m + (n + succ(K))
= m + succ(n + K)
= succ(m + (n + K))
= succ((m + n) + K)
= (m + n) + succ(K)
Distributivgesetz.
Induktionsanfang:
k·(m + 0) = k·m = k·m + 0 = k·m + k·0
Induktionsvoraussetzung:
Es gelte k·(m + N) = k·m + k·N für ein N ∈∈ ℕ.
Induktionsschluss:
k·(m + succ(N))
= k·succ(m + N)
= k + k·(m + N)
= k·(m + N) + k
= (k·m + k·N) + k
= k·m + (k·N + k)
= k·m + (k + k·N)
= k·m + k·succ(N)
Assoziativgesetz bezüglich der Multiplikation.
Induktionsanfang:
m·(n·0) = m·n = (m·n)·0
Induktionsvoraussetzung:
Es gelte m·(n·K) = (m·n)·K für ein K ∈∈ ℕ.
Induktionsschluss:
m·(n·succ(K))
= m·(n + (n·K))
= (m·n) + m·(n·K)
= (m·n) + ((m·n)·K)
= (m·n)·succ(K)
Neben den bisher bewiesenen Rechengesetzen sind noch die sogenannten Kürzungsregeln wichtig:
![]() V6
(Kürzungsregeln)
V6
(Kürzungsregeln)
Für alle x,y ∈∈ ℕ
gelten die Regeln
(N1)
x + n = y + n ⇔ x = y
mit n ∈∈ ℕ
(N2)
x · n = y · n ⇔ x = y
mit n ∈∈ ℕ und n ǂ 0.
Beweis:
(N1):
Seien x und y irgendwelche natürliche Zahlen.
Induktionsanfang:
x + 0 = y + 0 ⇔ x = y wegen (A1)
Induktionsvoraussetzung:
Es gelte x + m = y + m ⇔
x = y für ein m ∈∈ ℕ.
Induktionsschluss:
Es ist zu zeigen, dass x + succ(m) = y + succ(m) ⇔ x = y.
„⇐“:
x = y
⇒ x + m = y + m nach Induktionsvoraussetzung
⇒ succ(x + m) = succ(y + m),
denn succ ist eine Abbildung
⇒ x + succ(m) = y + succ(m)
„⇒“:
x + succ(m) = y + succ(m)
⇒ succ(x + m) = succ(y + m)
⇒ x + m = y + m, denn die Abbildung
succ ist injektiv
⇒ x = y nach Induktionsvoraussetzung
(N2) lässt sich auf analoge Art beweisen.
Die Regeln (N1) und (N2) spielen zum Beispiel eine wesentliche Rolle, wenn es darum geht zu zeigen, dass die Gleichungen von der Form m + x = n bzw. m · x = n mit vorgegebenen Zahlen m und n im Falle der Lösbarkeit eindeutig lösbar sind (siehe: Gleichungen (G1) und (G2) im Kapitel Zahlen).
Die Wohlordnung der natürlichen Zahlen
![]()
Mit Hilfe der Rechenregeln bezüglich der Addition auf ℕ kann man zeigen,
dass sich die natürlichen Zahlen ordnen
lassen. Hierzu ist zunächst eine passende Relation auf ℕ
zu definieren:
Seien m,n ∈∈ ℕ. Dann wird gesetzt:
m ≤ n ⇔def ∃p ∈∈ ℕ: m + p = n
In Worten: m ist genau dann kleiner oder gleich n, wenn eine natürliche Zahl p existiert mit der Eigenschaft, dass m + p = n.
Wenn für zwei natürliche Zahlen m und n m ≤ n und m ǂ n gilt, dann schreibt man: m < n.
![]() V7
V7
Für alle natürlichen Zahlen n gilt
0 ≤ n.
Beweis:
Induktionsanfang:
Es gilt 0 + 0 = 0, also ist 0 ≤ 0.
Induktionsvoraussetzung:
Es gelte 0 ≤ m für ein m ∈ ℕ.
Induktionsschluss:
0 ≤ m
⇒ 0 + p = m mit passend gewähltem
p ∈∈ ℕ
⇒ (0 + p) + succ(0) = m + succ(0)
⇒ 0 + (p + succ(0)) = m + succ(0)
⇒ 0 ≤ m + succ(0)
Mit (m + succ(0)) = succ(m + 0) = succ(m) folgt die Behauptung.
0 ist also die kleinste natürliche Zahl.
![]() V8
V8
Es gilt
für alle n ∈∈ ℕ
n < succ(n).
Beweis:
Nach Axiom (III) hat 0 kein Urbild unter der Abbildung succ.
Deswegen gilt
succ(0) ǂ 0.
Mit der oben bewiesenen Rechenregel n + succ(k) = succ(n + k) für alle k,n ∈∈ ℕ folgt insbesondere n + succ(0) = succ(n + 0) und damit
succ(n) = n + succ(0) für alle n ∈∈ ℕ.
Aus der Definition von „≤“ folgt wegen succ(0) ǂ 0 die Behauptung.
![]() V9
V9
Mit der Relation ≤ ist die Menge der natürlichen Zahlen wohlgeordnet.
Beweis:
Seien im Folgenden k,m,n ∈∈ ℕ
beliebig gewählt.
(i) Transitivität:
k ≤ n und n ≤ m
⇒ k + p1 = n und n
+ p2 = m mit passend gewählten p1,p2 ∈∈ ℕ
⇒ (k + p1) + (n + p2) = m + n
⇒ (k + (p1 + p2)) + n = m + n
⇒ k + (p1 + p2) = m
⇒ k ≤ m
(ii) Identitivität:
m ≤ n und n ≤ m
⇒ m + p1 = n und n
+ p2 = m mit passend gewählten p1,p2 ∈∈ ℕ
⇒ (m + p1) + (n + p2) = m + n
⇒ (m + n) + (p1 + p2) = m + n
⇒ (m + n) + (p1 + p2) = (m + n) + 0
⇒ p1 + p2 = 0
⇒ p1 ≤ 0
⇒ p1 = 0, denn 0 ist das kleinste Element in
ℕ
⇒ m = n
(iii) Reflexivität:
n + 0 = n
⇒ n ≤
n denn 0 ∈∈ ℕ.
(iv) Konnexität:
zu zeigen: k ≤ n oder
n ≤ k
für alle n,k ∈∈ ℕ.
Sei k ∈∈ ℕ
beliebig, aber fest gewählt.
Induktionsanfang:
Es gilt 0 ≤ k
für alle k ∈∈ ℕ.
Induktionsvoraussetzung:
Es gelte k < m
oder m < k oder
m =
k für ein m ∈∈ ℕ.
Induktionsschluss:
Fall 1: k < m
Dann gilt k < m < succ(m)
und es folgt
k < succ(m) wegen (i).
Fall 2: m < k
∃p ∈∈ ℕ: m + p = k
Wenn p = succ(0), so folgt
k = succ(m + 0) = succ(m);
wenn p ǂ succ(0), so folgt
k = m + succ(q) mit q ǂ 0.
⇒ k = succ(m
+ q)
⇒ k = q + succ(m)
⇒ succ(m) < k.
Fall 3: m = k
⇒ k < succ(m).
(v) Jede nichtleere Teilmenge von ℕ hat ein
kleinstes Element.
ℕ selbst hat ein kleinstes Element, nämlich 0.
Sei nun T ⊂ ℕ irgendeine nichtleere Teilmenge von
ℕ.
Induktionsanfang:
Angenommen, T hat nur ein einziges Element t.
Dann ist t ≤
t und t ist trivialerweise kleinstes Element von T.
Induktionsvoraussetzung:
Sei T ⊂ ℕ eine Menge natürlicher Zahlen mit m
Elementen und einem kleinsten Element,
es gibt also ein nmin ∈∈ T
mit nmin ≤ x für alle
x ∈∈ T.
Induktionsschluss:
Sei nun p irgendeine natürliche Zahl mit p ∉∉ T.
Dann gilt entweder p < nmin oder nmin < p, weil die
natürlichen Zahlen linear geordnet sind.
In der (m+1)-elementigen Menge T* = T ∪ { p } ist demzufolge unter Beachtung der Induktionsvoraussetzung entweder nmin
oder p kleinstes Element.
![]() V10
V10
Sei k eine beliebig gewählte natürliche Zahl. Dann existiert keine natürliche Zahl n
mit k < n < succ(k).
Beweis:
Sei k ∈∈ ℕ
beliebig gewählt. Angenommen, es existiert eine natürliche Zahl n mit k < n < succ(k).
Dann gibt es s,t ∈∈ ℕ
mit 0 < s und 0 < t,
so dass
n = k + s und
succ(k) = n + t
⇒ succ(k) = k
+ s + t
⇒ k + succ(0) = k
+ s + t
⇒ succ(0) = s
+ t
Da s ǂ 0 und t ǂ 0 gibt es s* und t* mit succ(s*) = s und succ(t*) = t.
⇒ 0 + succ(0) = s* + succ(0) + t* + succ(0)
⇒ 0 = s* + succ(0) + t*
⇒ 0 > succ(0)
Widerspruch! Es folgt die Behauptung.
Jetzt erst (!) ist bewiesen, dass es möglich ist, alle natürlichen Zahlen „der Reihe nach wie folgt aufzuschreiben“:
0 < succ(0) < succ(succ(0)) < succ(succ(succ(0))) < ...
Jeder, der die natürlichen Zahlen gut kennt, wird über die Resultate der vorstehenden Beweise nicht wirklich überrascht sein: Man kann die natürlichen Zahlen der Reihe nach abzählen und mit 0 geht es los. (Der Name der ersten natürlichen Zahl ist im Hinblick auf die Natur der natürlichen Zahlen völlig belanglos; man könnte diese Zahl auch Null nennen, oder zero oder egal-wie.) Es gibt zwei Operationen auf ℕ, die Addition und die Multiplikation, und beide sind kommutativ und assoziativ. Außerdem gelten das Distributivgesetz k(m + n) = km + kn für alle k, m, n ∈∈ ℕ sowie ein paar andere nützliche Rechenregeln. Es gibt ferner die Relation ≤ auf ℕ, mit der die natürlichen Zahlen wohlgeordnet sind.
Das alles ist nicht erstaunlich. Erstaunlich ist vielmehr, das alle diese Eigenschaften von ℕ tatsächlich allein mit den wenigen Axiomen (I) bis (IV) zusammenfassend und vollständig beschreibbar sind. Man erschließt sich diese Eigenschaften der Reihe nach im Wesentlichen mit einem Beweisprinzip, und dies ist das Prinzip der vollständigen Induktion.
Bemerkenswert ist auch, dass sich alle Gesetze in ℕ samt ihrer Beweise formulieren lassen, ohne die natürlichen Zahlen in irgendeiner Weise bezeichnen zu müssen, mit Ausnahme der kleinsten natürlichen Zahl. Um in ℕ unter Benutzung dieser Gesetze praktisch rechnen zu können, muss man natürlich Namen für die natürlichen Zahlen erfinden.
Die Idee, die natürlichen Zahlen mit Hilfe von dezimalen Zahlzeichen zu bezeichnen, stammt ursprünglich aus Indien. Der persische Mathematiker Abu Ja'far Muhammad ibn Musa al-Chwarizmi (etwa 780−850) hat das Dezimalsystem in seinem berühmten Werk hisab al-jabr wal-muqabalah verwendet. Danach hat es noch viele Jahrhunderte gedauert, bis das indische Dezimalsystem auch in Europa genutzt wurde.
Man benötigt zur Darstellung der natürlichen Zahlen im Dezimalsystem zehn Zahlzeichen, die je nach Sprache bzw. Schrift ganz unterschiedlich aussehen können. Beispiele:

Mit der Definition
1 =def succ(0)
ergibt sich aufgrund der Regel succ(k) = k + succ(0)
succ(k) = k + 1 für alle k ∈∈ ℕ.
Also kann man schreiben:
2 =def 1 + 1; 3 =def 2 + 1;
4 =def 3 + 1;
5 =def 4 + 1;
6 =def 5 + 1; 7 =def 6 + 1;
8 =def 7 + 1;
9 =def 8 + 1;
Im Dezimalsystem haben die zehn Zahlzeichen zwei unterschiedliche Bedeutungen: zum einen dienen sie dazu, die ersten zehn natürlichen Zahlen zu bezeichnen, zum anderen benutzt man sie zur Bezeichnung aller weiteren natürlichen Zahlen, wobei sie als Ziffern abhängig von ihrer Stelle innerhalb der die natürlichen Zahlen beschreibenden Ziffernfolgen verschieden interpretiert werden.
Die erste 2-stellige natürliche Dezimalzahl ist die Zahl 10:
10 =def 9 + 1
Um fortfahren zu können, wird der Begriff der Zehnerpotenz benötigt:
Ein Ausdruck der Form 10i heißt Zehnerpotenz und wird wie folgt induktiv definiert:
100 =def
1
10i+1 =def 10·10i
für alle i ∈∈ ℕ.
![]() V11
V11
Mit Hilfe der Zehnerpotenzen kann jede natürliche Zahl z ∈∈ ℕ wie folgt dargestellt werden:
z = z0·100 + z1·101 +...+ zn−1·10n−1.
Hierbei ist jedes der zi eine der Zahlen 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. (n−1) ist die natürliche Zahl, für die
(n−1) + 1 = n
gilt.
Beweis:
Induktionsanfang:
Es gilt 0 = 0·1 = 0·100.
Induktionsvoraussetzung:
Sei z ∈∈ ℕ dargestellt als
n-stellige Dezimalzahl, das heißt,
es gelte z = z0·100 + z1·101 +...+ zn−1·10n−1
mit n ∈∈ ℕ.
z0, z1, ..., zn−1
∈∈ {0, 1, 2, ..., 9} und
zn−1 ǂ 0.
Induktionsschluss:
Es ist zu zeigen, dass (z+1) auf die gleiche Art wie z dargestellt werden
kann.
Fall 1: z0 ǂ 9.
Dann gilt
z+1
= 1+(z0·100+z1·101+...+zn−1·10n−1) wegen der Kommutativität
bezüglich „+“
= (1·100+z0·100)+z1·101+ ...+zn−1·10n−1 wegen der Assoziativität
bezüglich „+“
= (z0+1)·100+z1·101+...+zn−1·10n−1 wegen des
Distributivgesetzes in ℕ
= Z0·100 + z1·101 +...+ zn−1·10n−1
mit Z0 ∈∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Fall 2: z0 = 9 und z1 ǂ
9.
Dann gilt
z+1
= 1 + (9·100+z1·101+...+zn−1·10n−1)
= 10·100 + z1·101 +...+ zn−1·10n−1
= 101 + z1·101 +...+ zn−1·10n−1
= 0·100 + Z1·101 +...+ zn−1·10n−1
mit Z1 ∈∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Fall 3: z0 = z1 = ... = zi = 9
und zi+1 ǂ 9 mit 0 < i < n−1
Dann gilt
z+1
= 1 + (9·100 + 9·101 + ... + zi+1·10i+1 + ... + zn−1·10n−1)
= 0·100 +...+ 0·10i + (zi+1+1)·10i+1 +...+ zn−1·10n−1
= 0·100 +...+ 0·10i + Zi+1·10i+1 +...+ zn−1·10n−1
mit Zi+1 ∈∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
Fall 4: z0 = z1 = ... = zn−1 = 9
Dann gilt z+1 = 0·100+0·101+...+ 0·10n−1+1·10n.
Für z = z0·100 + z1·101 + ... + zn−1·10n−1 schreibt man abkürzend:
z = zn−1...z2z1z0.
In dem Ausdruck zn−1...z2z1z0 sind die
zi keine Zahlen, sondern Ziffern, also
Dezimalzeichen!
Beispielsweise ist 7132 = 2·100 + 3·101 + 1·102 + 7·103.
Im Kapitel Algorithmus wird unter anderem dargestellt, wie und warum das Verfahren der schriftlichen Multiplikation von Dezimalzahlen funktioniert.
Für succ(0), den Nachfolger der kleinsten natürlichen Zahl 0, haben wir die Bezeichnung „1“ hingeschrieben.
![]() V12
V12
Es gilt
n·1 = n für alle n ∈∈ ℕ.
Beweis:
Für alle n ∈∈ ℕ gilt
n·1
= n·succ(0)
= muln(succ(0))
= addn(muln(0)) wegen (M2)
= addn(0) wegen (M1)
= n + 0
= n
![]() Summe der Quadratzahlen
von 0 bis n
Summe der Quadratzahlen
von 0 bis n
Sei n ∈∈ ℕ. Dann gilt für die
Summe der ersten n+1 Quadratzahlen:
n∑k = 0k2 = n(n+1)(2n+1)6.
Beweis:
Induktionsanfang:
Die Behauptung ist für n = 0 offensichtlich richtig.
Induktionsvoraussetzung:
Sei nun angenommen, dass die Behauptung für eine beliebige natürliche
Zahl n gilt.
Induktionsschluss:
Es ist zu zeigen, dass die Behauptung für n+1 ebenfalls wahr ist.
Zunächst hat man
n+1∑k = 0k2 = n∑k = 0k2 + (n+1)2
=
n(n+1)(2n+1)6 +
(n+1)2
= (2n3+3n2+n)
+ (6n2+12n+6)6
= 2n3+9n2+13n+66
Es gilt
(n+1)((n+1) + 1)(2(n+1) + 1)
= (n+1)(n+2)(2n+3)
= 2n3 + 9n2 + 13n + 6,
womit die Behauptung folgt.
![]() Binomischer Lehrsatz
Binomischer Lehrsatz
Für beliebige Zahlen a und b und für alle natürlichen
Zahlen n gilt
(a + b)n = n∑k = 0(nk)· an−k·bk .
Hierbei ist
(nk) = n·(n−1)·(n−2)·...·(n−k+1)1·2·...·k
der Binomialkoeffizient von n über k für alle k ≥ 1. Speziellerweise wird definiert:
(n0) = 1 für alle n ∈∈ ℕ.
Man rechnet schnell nach, dass
(nk)
= n!k!(n−k)!
.
Beweis des binomischen Lehrsatzes:
Auf Grund der Definition des Binomialkoeffizienten gilt für alle natürlichen
Zahlen n und k mit k ≤ n
(nk) +
(nk + 1)
= (nk) +
(nk)· n − kk + 1
= (nk)· (1 + n − kk + 1)
= (nk)· n + 1k + 1
= (n + 1k + 1).
Hiermit hat man die wichtige Rechenregel
(nk) + (nk + 1) = (n + 1k + 1).
Mit Hilfe dieser Rechenregel kann nun der binomische Satz bewiesen werden.
Induktionsanfang:
Für die Zahl 2 ist der binomische Satz wohlbekannt: (a + b)2 = a2 + 2ab + b2.
Der
Satz ist auch für die Zahlen 1 und 0 richtig: (a + b)1 = a1b0 + b1a0 und (a + b)0 = a0b0.
Induktionsvoraussetzung:
Sei nun angenommen, dass der binomische Satz richtig
ist für irgendeine natürliche Zahl m. Das heißt, es gilt:
(a + b)m = m∑k = 0(mk)· am−k·bk .
Induktionsschluss:
Multiplikation mit (a + b) auf beiden Seiten liefert
(a + b)m+1 = (a + b) ·m∑k = 0(mk)· am−k·bk .
Ausmultiplizieren der rechten Seite ergibt den Ausdruck
am+1 +(m1)· am·b +(m2)· am−1·b2 + ...
... +(mm−1)· a2·bm−1 +(mm)· a·bm + ...
... +(m0)· am·b +(m1)· am−1· b2 + ...
... +(mm−2)· a2·bm−1 +(mm−1)· a·bm + bm+1
Unter Verwendung der obenstehenden Rechenregel lässt sich dieser Ausdruck umformen zu
m+1∑k = 0(m+1k)· am+1−k·bk,
was zu beweisen war.
Die Binomialkoeffizienten der Rechenausdrücke (a + b)0, (a + b)1, (a + b)2, (a + b)3, ... ergeben, wenn man sie in entsprechender Form hinschreibt, das sogenannte „Pascal’sche Dreieck“, welches bereits von den persischen Mathematikern Muhammad al-Karadschi (953−1029) und Omar Khayyam (1048−1131) beschrieben und untersucht wurde:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5
1
1 6 15 20 15 6 1
1 7 21 35 25 21 7 1
...
![]() Ungleichung von Bernoulli
Ungleichung von Bernoulli
Ist 1+h eine positive reelle Zahl, so gilt
(1 + h)n ≥ 1 + n·h für alle n ∈∈ ℕ*.
Beweis:
Induktionsanfang:
Es gilt (1 + h)1 = 1 + 1·h.
Induktionsvoraussetzung:
Es gelte (1 + h)m
≥ 1 + m·h für irgendeine natürliche Zahl m, die größer oder gleich 1 ist.
Induktionsschluss:
Aus der Induktionsannahme folgt durch Multiplikation mit (1 + h)
(1 + h)m+1 ≥ (1 + h)(1 + mh) = m·h2 + (m + 1)·h + 1.
Wegen m·h2 > 0 hat man (1 + h)m+1 ≥ (m + 1)·h + 1, was zu zeigen
war.
![]() Der
Turm von Hanoi
Der
Turm von Hanoi
Auf dem ersten von drei Stäben liegen n Scheiben - der Größe nach geordnet - übereinander.
Der gesamte Scheibenturm soll vom ersten auf den dritten Stab umgesetzt werden und zwar so,
dass nacheinander jede Scheibe einzeln von einem Stab auf einen anderen
gelegt wird. Das Spiel ist beendet, wenn zum Schluss der gesamte Scheibenturm in der ursprünglichen
Anordnung der Scheiben auf dem dritten Stab liegt. Es gilt zusätzlich die Regel, dass
während des Spiels eine Scheibe nur dann umgesetzt werden darf, wenn die
nach der Umsetzung unter ihr liegende Scheibe größer ist als sie selbst. Wie
groß ist die minimale Anzahl der Umsetzungen?
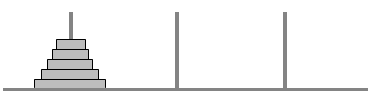
Behauptung: Die Anzahl der Umsetzungen ist mindestens gleich 2n − 1.
Beweis:
Induktionsanfang:
Falls n = 1, braucht man nur eine Umsetzung und es ist 1 = 21 − 1.
Induktionsvoraussetzung:
Sei angenommen, dass die Behauptung für m Scheiben bereits bewiesen ist,
wobei m eine beliebige, aber fest gewählte natürliche Zahl darstellt.
Induktionsschluss:
Auf dem ersten Stab sollen nun (m + 1) Scheiben liegen. Die gestellte
Aufgabe ist nur dann lösbar, wenn es während des Spiels zu folgender
Situation kommt:

Die größte Scheibe kann und muss jetzt direkt vom ersten Stab auf den
dritten Stab umgesetzt werden, und zwar nachdem die zuvor über der größten
Scheibe liegenden m anderen Scheiben vom ersten Stab auf den mittleren Stab
umgesetzt worden sind, wofür man nach der Induktionsvoraussetzung mindestens
2m − 1 Schritte gebraucht hat. Wenn die größte Scheibe auf dem
dritten Stab liegt, braucht man für die Umsetzung der m Scheiben vom
mittleren auf den dritten Stab nochmals 2m − 1 Schritte, macht
alles zusammen 2·(2m − 1)+1 Schritte. Diese Argumentation ist
völlig unabhängig von der Wahl von m!
Es gilt 2·(2m − 1) + 1 = 2m+1 − 1, womit die
Behauptung bewiesen ist.
Die Folge der 2n − 1 Spielzüge kann man automatisiert ablaufen lassen, und zwar mit Hilfe eines rekursiven Algorithmus:
if (i > 0) {
move (i−1, a, c, b);
verschiebe oberste Scheibe von a nach c;
move (i−1, b, a, c);
}
}
Das Spiel „Turm von Hanoi“ ist 1883 vom Mathematiker Edouard Lucas (1842−1891) erfunden worden und wurde von ihm damals verkauft. In der Spielbeschreibung wurde der Turm von Hanoi (mit acht Scheiben) als verkleinerte Version des Turms von Brahma im Tempel der indischen Stadt Benares ausgewiesen. Der Turm von Brahma soll aus 64 goldenen Scheiben bestanden haben, die Schritt für Schritt gemäß der oben beschriebenen Regeln durch Tempelpriester umgelegt wurden. Martin Gardner schreibt dazu in seinem Buch Mathematische Rätsel und Probleme:
Bevor sie damit beendet sein werden, so sagte man, wird der Tempel in Staub zerfallen und die Welt wird mit einem Donnerschlag verschwinden. Das Untergehen der Welt mag fraglich sein, jedoch besteht wenig Zweifel am Zerfall des Tempels. Auf Grund der Formel 264 − 1 ergibt sich nämlich die 20-stellige Zahl 18.446.744.073.709.551.615. Unter der Annahme, daß die Priester Tag und Nacht arbeiten und in jeder Sekunde eine Scheibe umlegen, würden sie viele Milliarden Jahre brauchen, um ihre Arbeit zu vollenden.
