Wahrscheinlichkeit
 Niemand wird ernsthaft erwarten, dass diese Kugel irgendwann einmal aus dem Bildschirm kullern wird. Dies ist nach unseren
bisherigen Erfahrungen ein unmögliches Ereignis, und die Wahrscheinlichkeit, die wir diesem
Ereignis zuordnen, ist gleich 0.
Niemand wird ernsthaft erwarten, dass diese Kugel irgendwann einmal aus dem Bildschirm kullern wird. Dies ist nach unseren
bisherigen Erfahrungen ein unmögliches Ereignis, und die Wahrscheinlichkeit, die wir diesem
Ereignis zuordnen, ist gleich 0.
Andererseits sind wir nach dem, was wir zumindest in unseren geografischen
Breiten bislang erlebt haben, ganz sicher, dass auch morgen früh wieder die
Sonne aufgehen wird (sicheres Ereignis) und erwarten dies
deshalb mit der Wahrscheinlichkeit 1.
Die Wahrscheinlichkeit für irgendein zukünftiges Ereignis E liegt demnach irgendwo zwischen 0 und 1.
0 ≤ P(E) ≤ 1
Wahrscheinlichkeitsaussagen beziehen sich zwar immer auf einzelne zukünftige Ereignisse als mögliche Resultate eines Zufallsexperimentes, sind aber nur dann sinnvoll, wenn sie auf Beobachtungen beruhen, die während einer sehr großen Zahl von Durchläufen des gleichen Zufallsexperimentes zuvor gemacht worden sind.
Nach dem Drücken des Buttons "Würfeln" wird eine in JavaScript geschriebene Simulation gestartet, die dem n-maligen Würfeln eines idealen Würfels entspricht (→ Quelltext). Es wird gemessen, wie oft die einzelnen Augenzahlen gewürfelt werden (absolute Häufigkeiten). Dividiert man die absoluten Häufigkeitswerte jeweils durch n (Umfang des Zufallsexperiments), so erhält man die zugehörigen relativen Häufigkeiten.
Die sich ergebenden Häufigkeitswerte (habs und hrel) werden in der Tabelle ausgegeben und anschließend in einem Häufigkeitsdiagramm veranschaulicht. Für n können Werte zwischen 1 und 999999 eingegeben werden.
Mit größer werdendem n stabilisieren sich die relativen Häufigkeiten (empirisches Gesetz der großen Zahlen). Die relative Häufigkeit einer bestimmten Augenzahl beim Würfeln eines idealen Würfels ist (unabhängig von der Augenzahl) bei sehr, sehr großem Umfang des Zufallsexperimentes (mit einer gewissen Abweichung) etwa gleich 16.
Allgemein gilt: Der zu erwartende relative Häufigkeitswert eines Ereignisses E bei sehr, sehr, sehr großem Umfang des betreffenden Zufallsexperimentes entspricht dem Wahrscheinlichkeitswert P(E) dieses Ereignisses. (Die Bezeichnung „P“ kommt vom ersten Buchstaben des englischen Wortes probability.)
Die Wahrscheinlichkeit dafür, dass beim nächsten Wurf eines idealen Würfels eine bestimmte Augenzahl gewürfelt wird, beträgt 16. Aus dieser Aussage lässt sich nicht schließen, was als nächstes tatsächlich gewürfelt wird. Es ist beispielsweise durchaus möglich, dass die Augenzahl „2“ dreimal hintereinander gewürfelt werden wird. Die Wahrscheinlichkeit hierfür ist allerdings eher klein: 16·16·16, also etwa gleich 0,0046, mit anderen Worten: Wenn ein idealer Würfel insgesamt 10000mal hintereinander zufällig gewürfelt wird, so ist hierbei zu erwarten, dass etwa 46mal die Augenzahl „2“ dreimal hintereinander gewürfelt wird.
Zu diesem Zufallsexperiment gehört die Ergebnismenge
S = {(1;1), (1;2), (1;3), ..., (2;1), (2;2), ... (6;6)}.
Alle 36 Ergebnisse dieses Zufallsexperimentes sind gleichwahrscheinlich (zumindest dann, wenn ideale Würfel verwendet und diese unter gleichen Bedingungen geworfen werden), das heißt, es ist ein sogenanntes Laplace-Experiment. (Beim Würfeln mit einem Würfel handelt es sich auch um ein Laplace-Experiment, was durch das Simulationsexperiment bestätigt werden konnte.)
Jede nichtleere Teilmenge von S entspricht einem möglichen Ereignis. Zum Beispiel gehört zum Ereignis "Ein Pasch wird gewürfelt" die Menge {(1;1), (2;2), (3;3), ... (6;6)}. Man sagt, ein bestimmtes Ereignis „ist eingetreten“, wenn das beobachtete Ergebnis ein Element der zu diesem Ereignis gehörenden Menge ist.
Die Berechnung von Wahrscheinlichkeiten im Zusammenhang von Laplace-Experimenten ist nicht schwierig. Für jedes Ereignis E eines Laplace-Experimentes gilt
P(E) = |E||S|.
Hierbei ist |E| die Anzahl der Elemente in E (d.h. die Anzahl aller günstigen Ergebnisse) und |S| die Anzahl der Elemente in S (d.h. die Anzahl aller möglichen Ergebnisse). Pierre-Simon Laplace (1749−1827) schrieb hierzu in seinem 1814 erschienenen Werk Essai philosophique sur les probabilités (Philosophischer Versuch über die Wahrscheinlichkeiten):
Der hier gegebene Begriff der Wahrscheinlichkeit setzt voraus, dass, wenn man die Zahl der günstigen Fälle und die aller möglichen Fälle in gleichem Verhältnis wachsen lässt, die Wahrscheinlichkeit dieselbe bleibt. Um sich davon zu überzeugen, stelle man sich zwei Urnen A und B vor, von denen die erste vier weisse und zwei schwarze Kugeln enthält, und die zweite nur zwei weisse und eine schwarze Kugel einschliesst. Nun denke man sich, dass die zwei schwarzen Kugeln der ersten Urne an einen Faden gebunden sind, der in dem Momente reisst, wo man die eine von ihnen ergreift, um sie herauszuziehen, und dass die vier weissen Kugeln zwei ähnliche Systeme bilden. Alle Chancen, welche bewirken, dass eine der Kugeln des schwarzen Systems ergriffen wird, werden eine schwarze Kugel herausbringen. Wenn man sich jetzt vorstellt, dass die Fäden, welche die Kugeln verbinden, nicht reissen, so ist klar, dass die Zahl aller möglichen Chancen sich ebenso wenig ändern wird als die dem Herausziehen schwarzer Kugeln günstigen Chancen; nur wird man aus der Urne zwei Kugeln auf einmal herausziehen; die Wahrscheinlichkeit, eine schwarze Kugel aus der Urne herauszuziehen, wird also dieselbe sein wie früher. Aber dann hat man augenscheinlich den Fall der Urne B mit dem einzigen Unterschiede, dass die drei Kugeln dieser letzteren Urne ersetzt sind durch drei Systeme von je zwei Kugeln, die unveränderlich mit einander verbunden sind.
Die Idee, die Wahrscheinlichkeit eines Ereignisses mit einem Bruch in der oben beschriebenen Weise anzugeben, stammt nicht von Laplace. Im von Abraham de Moivre (1667−1754) 1718 veröffentlichten Werk The DOCTRINE OF CHANCES (dem ersten Lehrbuch der Wahrscheinlichkeitstheorie überhaupt) lesen wir in der Einführung:
The Probability of an Event is greater, or less,
according to the number of Chances by which it may Happen, compar’d
with the number of all the Chances, by which it may either Happen or Fail.
Thus, If an Event has 3 Chances to Happen, and 2 to Fail; the Probability of
its Happening may be estimated to be
35, and the Probability of its Failing
25.
Therefore, if the Probability of Happening and Failing are added together,
the Sum will always be equal to Unity.
Von den in der folgenden Tabelle definierten Ereignissen A, B, C, D und S können im darunter stehenden Gitterdiagramm jeweils zwei Ereignisse dargestellt werden. Hierbei werden gleichzeitig die zugehörigen Wahrscheinlichkeitswerte berechnet und ausgegeben. (Diese Animation ist mit JavaScript programmiert.)
Die Beispiele im Gitterdiagramm führen auf weitere Regeln zur Berechnung von Wahrscheinlichkeiten. Die erste Regel (spezieller Additionssatz) lautet:
P(A∪B) = P(A) + P(B),
falls A∩B = { }
Mit A∪B wird hierbei dasjenige Ereignis bezeichnet, welches eintritt,
falls A oder B eintritt und A∩B repräsentiert
dasjenige Ereignis, das eintritt, wenn A und B eintritt. Man
kann das auch anders ausdrücken: Das Ereignis A∪B tritt genau dann ein, wenn mindestens
eines der Ereignisse A oder B eintritt, während das Ereignis A∩B genau dann eintritt, wenn sowohl A, als auch B
eintritt. Die Aussage A∩B = { }
bedeutet, dass die Ereignisse A und B kein Ergebnis gemeinsam haben. In
diesem Fall heißen die Ereignisse A und B unvereinbar.
Sind A und B nicht miteinander unvereinbar, so gilt statt des speziellen Additionssatzes allgemeiner:
P(A∪B) = P(A) + P(B) − P(A∩B).
Die anschauliche Bedeutung der Ausdrücke A∪B
und A∩B ergibt sich schon aus den Beispielen im
Gitterdiagramm, sie lässt sich aber noch allgemeiner verstehen, und zwar mit
Hilfe der sogenannten Venn-Diagramme. A und B werden hierbei als Teilmengen einer
Grundmenge S aufgefasst.
Ein Ergebnis s der Ergebnismenge S eines Zufallsexperimentes gehört genau
dann zu A∩B, wenn s zu A und zu B gehört. Zu A∪B
gehört ein Ergebnis s genau dann, wenn s zu A oder zu B gehört (das heißt,
wenn s entweder nur zu A oder nur zu B oder zu
A∩B gehört).
Der russische Mathematiker Andrei Nikolajewitsch Kolmogorow (1903−1987) hat gezeigt, dass alle Aussagen der Wahrscheinlichkeitsrechnung mathematisch streng bewiesen werden können, wenn lediglich drei Eigenschaften für die Wahrscheinlichkeit P axiomatisch festgelegt werden. Hierbei wird P verstanden als Abbildung der Potenzmenge einer vorgegebenen Ergebnismenge S auf das geschlossene Intervall [0; 1] ⊂ ℝ.
℘(S) = { A: A ⊆ S
} ist die Potenzmenge von S,
also die Menge aller
Teilmengen von S, einschließlich der leeren Menge { } und S selber. Die Definition von P lautet dann wie folgt.
Sei S die Menge aller möglichen Ergebnisse eines wohldefinierten
Zufallsexperimentes.
Dann heißt die Funktion
P:
℘(S)
→ [0; 1]
genau dann Wahrscheinlichkeit, wenn Folgendes gilt:
| (K1) | P(S) = 1 |
| (K2) | 0 ≤ P(E) ≤ 1 für alle E ⊆ S |
| (K3) |
P(A∪B) = P(A) + P(B), falls A, B ⊆ S und A∩B = { } |
S nennt man die Ergebnismenge des jeweiligen Zufallsexperimentes; die Teilmengen E der Ergebnismenge heißen Ereignismengen (oder kurz: Ereignisse).
Sei E irgendein Ereignis eines Zufallsexperimentes. Dann wird das Komplementärereignis von E, welches eintritt, wenn E nicht eintritt, mit E bezeichnet. Es gilt
P(E) = 1 − P(E).
Beweis:
Aus E∪E = S und E∩E = { } folgt wegen (K1) und (K3), dass
1 = P(S) = P(E∪E)
= P(E) + P(E).
Die Regel P(E) = 1 − P(E) ist für alle Ereignisse E ⊆ S
gültig, also auch speziell für S. Es folgt
P({ }) = 1 − P({ }) = 1 − P(S)
und man hat wegen (K1)
P( { } ) = 0.
Sind A und B Ereignismengen eines Zufallsexperimentes mit der Ergebnismenge S, so gilt
A ⊆ B ⇒ P(A) ≤ P(B)
und P(B∩A) = P(B) − P(A).
Beweis:
Wegen A ⊆
B folgt B = A ∪ (B∩A)
und es ist A ∩ (B∩A) = { }.
Unter Benutzung von (K3) folgt hieraus, dass
P(B) = P(A) + P(B∩A)
und damit P(B∩A) = P(B) − P(A).
P(A) ≤ P(B) folgt mit (K2).
Die Regel zur Berechnung der Wahrscheinlichkeiten von "Oder"-Ereignissen (allgemeiner Additionssatz),
P(A∪B) = P(A) + P(B) − P(A∩B),
ist im Rahmen von Laplace-Experimenten unmittelbar einleuchtend. Auf Grundlage der Kolmogorow’schen Axiome (K1), (K2) und (K3) kann man diesen Satz für alle möglichen Zufallsexperimente beweisen. Die Einschränkung auf Laplace-Experimente (S ist eine endliche Menge und alle Ergebnisse sind gleichwahrscheinlich) kann fallen gelassen werden.
Beweis:
Für A, B ⊆ S gilt stets A∪B = A ∪ (A∩B)
mit A ∩ (A∩B) = { }.
(K3) liefert
(●) P(A∪B) = P(A) + P(A∩B).
Aus B = (A∩B) ∪
(A∩B)
folgt wegen (A∩B) ∩ (A∩B) = { } aus demselben Grund
(●●) P(B) = P(A∩B)
+ P(A∩B).
Unter Benutzung der Gleichungen (●) und (●●) folgt
P(A∪B) = P(A) + P(B) − P(A∩B),
was zu beweisen war.
Die Regel zur Berechnung der Wahrscheinlichkeiten von "Und"-Ereignissen (Multiplikationssatz) lautet
P(A∩B)
= P(A/B)·P(B).
PB(A) = P(A/B) heißt bedingte Wahrscheinlichkeit von A unter der Bedingung B, das ist die Wahrscheinlichkeit des Ereignisses A unter der Voraussetzung, dass das Ereignis B bereits eingetreten ist. Man rechnet leicht nach, dass die durch
PB(A) = P(A∩B)P(B)
definierte bedingte Wahrscheinlichkeit PB tatsächlich eine Wahrscheinlichkeit darstellt, das heißt, dass auch für PB die Kolmogorow’schen Axiome gelten.
In dem Fall, wo A und B voneinander stochastisch unabhängig sind, vereinfacht sich der Multiplikationssatz. Ein Ereignis A heißt stochastisch unabhängig vom Ereignis B genau dann, wenn P(A/B) = P(A/B). Das bedeutet, dass die Wahrscheinlichkeit dafür, dass A eintritt, unabhängig davon ist, ob B zuvor eingetreten ist oder eben nicht eingetreten ist. Mit Hilfe dieses Begriffs lässt sich der folgende wichtige Satz formulieren:
Zwei Ereignisse A und B eines Zufallsexperimentes sind genau dann voneinander stochastisch unabhängig, wenn
P(A∩B) = P(A)·P(B)
gilt.
Der Beweis dieses Satzes ist ein sogenannter
Äquivalenzbeweis, der in zwei Schritten
geführt wird.
Zunächst wird gezeigt, dass aus der ersten Aussage (stochastische
Unabhängigkeit zweier Ereignisse A und B) die zweite Aussage (P(A∩B) = P(A)·P(B)) folgt, danach wird die Umkehrung dieser Folgerung bewiesen. Für
die Durchführung dieser zwei Schritte wird zunächst gezeigt, dass die
Aussage
P(A) = PB(A)·P(B) + PB(A)·P(B)
immer wahr ist.
Beweis:
Für A, B
⊆ S
gilt in jedem Fall A = A∩S = A ∩ (B∪B) = (A∩B) ∪ (A∩B).
Wegen (A∩B) ∩
(A∩B)
= { } folgt mit (K3), dass P(A) = P(A∩B) + P(A∩B).
Nach Definition der
bedingten Wahrscheinlichkeit gilt
sowohl P(A∩B) = PB(A)·P(B)
als auch P(A∩B) = PB(A)·P(B).
Also hat man insgesamt die Aussage (●) P(A) = PB(A)·P(B) + PB(A)·P(B).
"⇒": Seien A und B stochastisch
unabhängig voneinander,
dann gilt nach Definition
PB(A) = PB(A)
und es folgt mit (●), dass
P(A) = PB(A)·(P(B) + P(B)) = PB(A)·P(S) = PB(A).
Hieraus folgt P(A∩B) = PB(A)·P(B) = P(A)·P(B).
"⇐": Umgekehrt gelte jetzt P(A∩B) = P(A)·P(B).
Dann folgt P(A) = PB(A) und mit der Gleichung (●)
ergibt sich, dass
PB(A) = PB(A)·P(B)
+ PB(A)·P(B)
⇒
PB(A)·(1 − P(B)) = PB(A)·P(B)
⇒
PB(A) = PB(A),
was zu beweisen war.
Die Berechnung von Wahrscheinlichkeiten ist sehr häufig mit kombinatorischen Problemen verknüpft. Eine alte Frage ist die nach der Wahrscheinlichkeit, sechs Richtige im Lotto zu gewinnen. Um solche Fragen lösen zu können, muss man mindestens die folgenden drei Aussagen verstanden haben, in denen zwei von 0 verschiedene natürliche Zahlen n und k vorkommen mit der Eigenschaft, dass k immer kleiner oder gleich n ist. Die Aussagen lauten:
(1) n paarweise verschiedene Dinge kann man auf n! verschiedene Arten anordnen.
(2) Aus n paarweise verschiedenen Dingen kann man unter Berücksichtigung der Reihenfolge
k Dinge auf n·(n−1)·(n−2)·...·(n−k+1)
verschiedene Arten auswählen.
(3) Aus n paarweise verschiedenen Dingen kann man
ohne Berücksichtigung der Reihenfolge k Dinge
auf n·(n−1)·(n−2)·...·(n−k+1)k!
verschiedene Arten auswählen.
Hierbei ist der Ausdruck n! (n Fakultät) wie folgt definiert:
n! = 1, wenn n = 0;
(n+1)! = n!·(n+1) sonst
Zum Beispiel ist 3! = 1·2·3 = 6 oder 5! = 1·2·3·4·5 = 120.
Für den komplizierten Ausdruck, der in der Aussage (3) vorkommt, gibt es eine abkürzende Bezeichnung. Man nennt diesen Ausdruck Binomialkoeffizient von n über k.
(nk) = n·(n−1)·(n−2)·...·(n−k+1)1·2·...·k
Für den Fall k = 0 wird für alle natürlichen Zahlen n speziell definiert, dass Folgendes gelten soll:
(n0) = 1
Beispielsweise gilt (75) = 7·6·5·4·31·2·3·4·5 = 21.
Beweis der Aussagen (1), (2) und (3):
In der Aussage (1) geht es um folgende Fragestellung: n voneinander
unterscheidbare Objekte sollen auf n Plätze verteilt werden. Wieviele
voneinander verschiedene Möglichkeiten hat man?
Der Fall n = 1 ist einfach: Es gibt natürlich nur eine einzige
Möglichkeit.
![]()
Bei n = 2 gibt es immerhin schon 2 verschiedene Möglichkeiten:
![]()
![]()
Im Falle n = 3 haben wir für den ersten Platz drei mögliche Belegungen. Wenn der erste Platz bereits belegt ist, dann haben wir für die verbleibenden zwei Plätze noch zwei Möglichkeiten, die übrig gebliebenen zwei Objekte zu verteilen; das macht dreimal zwei Möglichkeiten, also insgesamt 6 Möglichkeiten.
![]()
![]()
![]()
Im Falle n = 4 haben wir für den ersten Platz vier mögliche Belegungen. Wenn der erste Platz bereits belegt ist, dann haben wir für die verbleibenden drei Plätze noch sechs Möglichkeiten, die übrig gebliebenen drei Objekte zu verteilen (das haben wir eben ausgerechnet). Also gibt es hier viermal sechs Möglichkeiten, also insgesamt 24 Möglichkeiten.
![]()
![]()
![]()
![]()
Für n = 1, n = 2, n = 3 und n = 4 ist also die Aussage (1) wahr. Wie geht es jetzt weiter? Schritt für Schritt genauso. Im Falle n = 5 gibt es insgesamt 120 Möglichkeiten, im Falle n = 6 sind es 720, u.s.w.
Mal angenommen, wir hätten bis zu einer gewissen Zahl m weitergemacht, dann wissen wir sicher, dass sich m Objekte auf m! verschiedene Arten auf m Plätze verteilen lassen. Im nächsten Schritt (das heißt für n = m+1) haben wir für den ersten Platz m+1 mögliche Belegungen. Wenn der erste Platz bereits belegt ist, dann haben wir für die verbleibenden m Plätze noch m! Möglichkeiten, die übrig gebliebenen m Objekte zu verteilen. Also gibt es jetzt m+1mal m! Möglichkeiten, also insgesamt (m+1)! Möglichkeiten.
Dieser Schluss von n = m auf n = m+1 ist für jede beliebige natürliche Zahl möglich, also ist hiermit die Aussage (1) bewiesen. Einen solchen Beweis nennt man in der Mathematik "Beweis mit vollständiger Induktion über n" oder kurz Induktionsbeweis. Man braucht für einen solchen Beweis einen Induktionsanfang (der im vorstehenden Beispiel bereits damit gegeben ist, dass die behauptete Aussage für n = 1 bestätigt wurde) und die Induktionsvoraussetzung (das ist die Annahme, dass die behauptete Aussage bereits für n = m bewiesen worden ist), um dann den Induktionsschluss durchzuführen (das ist der Nachweis, dass mit der Induktionsvoraussetzung die behauptete Aussage auch für n = m+1 wahr ist) (siehe auch: Das Prinzip der vollständigen Induktion).
Auch die Aussage
(2) lässt sich mit vollständiger Induktion beweisen, und zwar über k.
Der Induktionsanfang ist mit k = 1 bei einer beliebigen, aber fest
gewählten positiven natürlichen Zahl n klar: Aus n paarweise verschiedenen Objekten kann man selbstverständlich auf n
verschiedene Arten ein Objekt auswählen.
Angenommen, die Aussage (2) sei für k = m bereits bewiesen.
Dann lassen sich aus n verschiedenen Dingen unter Berücksichtigung der
Reihenfolge m Dinge auf Nm verschiedene Arten auswählen mit
Nm = n·(n−1)·(n−2)·...·(n−(m−1)),
kurz geschrieben:
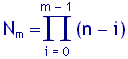
Alle Nm Kombinationsmöglichkeiten kann man darstellen in Form einer Tabelle mit Nm Zeilen und m Spalten. Jede dieser Zeilen lässt sich mit einem der (n−m) übrig gebliebenen Dinge zu einer neuen Zeile der Länge (m+1) kombinieren. Da alle Zeilen der Tabelle nach Induktionsannahme paarweise verschieden sind, gilt das Gleiche auch für die neu gebildeten Zeilen. Andererseits erhält man mit der Gesamtheit der so konstruierten neuen Zeilen alle möglichen Kombinationen von (m+1) Dingen aus insgesamt n vorhandenen Dingen. Nach Konstruktion sind dies insgesamt Nm·(n−m) Kombinationen, also folgt

und damit die Behauptung.
Aussage (3) folgt direkt aus Aussage (1) und Aussage (2).
Sei S die Ergebnismenge eines Zufallsexperimentes. Dann heißt eine Funktion
X: S → ℝ,
die jedem Ergebnis s ∈∈ S eine
reelle Zahl zuordnet, Zufallsvariable über S.
Sei xi ein Wert einer solchen Zufallsvariablen X und seien s1,
s2, ..., sk alle Ergebnisse, zu denen dieser Wert
xi gehört, dann schreibt man
P({s1, s2, ..., sk}) = P(X=xi).
Ist X eine Zufallsvariable über S, dann heißt die Funktion F, die jedem Wert xi von X den Wahrscheinlichkeitswert P(X = xi) zuordnet, Wahrscheinlichkeitsverteilung von X. Wenn X die Werte x1, x2, ..., sn annehmen kann, dann heißt die reelle Zahl E(X) mit
E(X) = x1·P(X=x1) + x2·P(X=x2) + ... + xn·P(X=xn)
der Erwartungswert von X. (Oft wird statt „E(X)“ auch „μ“ geschrieben.)
Beispiel. Anton und Bert spielen das Spiel "Eine Münze wird geworfen", und zwar dreimal hintereinander. Bert zahlt an Anton 1€, wenn höchstens einmal Wappen fällt; Anton zahlt an Bert 2€, wenn zweimal Wappen fällt; keiner von beiden zahlt, wenn dreimal Wappen fällt. Betrachten wir nun alle möglichen Spielergebnisse aus der Sicht von Anton und ordnen diesen die Geldbeträge zu, die Anton jeweils gewinnt, bzw. verliert, erhalten wir die folgende Zufallsvariable X:
Als Wahrscheinlichkeitsverteilung von X ergibt sich also:

E(X) = −0.25. Demnach wird sich das Spiel für Anton auf lange Sicht nicht lohnen, denn wegen des negativen Erwartungswertes ist das Spiel für ihn nicht fair. (Zu beachten ist, dass - wie in diesem Beispiel auch - E(X) in der Regel kein Wert von X ist.)
Endkontrolle von Computern
Von den in der Firma ElecExe hergestellten Computern sind erfahrungsgemäß
4% fehlerhaft. Bei der Endkontrolle wird ein fehlerhaftes Gerät mit der
Wahrscheinlichkeit 0,8 beanstandet. Es kommt durchaus vor, dass ein
einwandfreies Gerät beanstandet wird, und zwar mit der Wahrscheinlichkeit 0,1.
Wie groß ist die Wahrscheinlichkeit dafür, dass a) ein bei der Endkontrolle
beanstandetes Gerät auch tatsächlich fehlerhaft ist, und b) ein nicht
beanstandetes Gerät fehlerfrei ist?
Die in der Aufgabe genannten Eingangsdaten können in der folgenden mit JavaScript programmierten Tabelle verändert werden.
Lotto „6 aus 49“
Wie wahrscheinlich ist es (ohne Beachtung der Zusatzzahl) r Richtige im Lotto zu erzielen?
Lösung: Aus 49 Zahlen eines Lottofeldes kann man 6 Zahlen ohne Berücksichtigung der Reihenfolge auf N unterschiedliche Arten zum Ankreuzen auswählen mit
N = (496) = 13983816.
Das heißt, es gibt insgesamt fast vierzehn Millionen verschiedene Ankreuzmöglichkeiten. Das Ereignis "r Richtige" tritt genau dann ein, wenn r von den sechs angekreuzten Zahlen in der Glücksmaschine geworfen werden und (6−r) Zahlen nicht geworfen werden. Hierfür gibt es alles in allem
N(r) = N6,r·N43,6−r = (6r)·(436−r)
mögliche Kombinationen. Da alle 49 Zahlen mit gleicher Wahrscheinlichkeit
geworfen werden, handelt es sich beim Lottospiel um ein Laplace-Experiment.
Also ist die Wahrscheinlichkeit, bei einem Lottofeld genau r Richtige zu
erzielen, gleich
N(r)N.
Wenn mehrere Lottofelder ausgefüllt werden,
erhöht sich natürlich die Gewinnwahrscheinlichkeit. Sei z die Zahl der
ausgefüllten Lottofelder, dann ist zum Beispiel die Wahrscheinlichkeit
dafür, mindestens einmal genau r Richtige zu haben, gleich
P(r) = 1 − (1 − N(r)N)z.
Die Wahrscheinlichkeit bei z ausgefüllten Lottofeldern mindestens einmal mindestens r Richtige zu haben, beträgt
1 − (1 − N(r)+N(r+1)+...+N(6)N)z.
Diese Formeln gelten nur unter der Voraussetzung, dass alle Lottofelder unabhängig voneinander und zufällig angekreuzt werden!
Die folgenden Berechnungen (→ Quelltext) funktionieren mithilfe von JavaScript.
Die Wahrscheinlichkeit, bei einem ausgefüllten Lottofeld höchstens 3 Richtige zu erzielen, ist gleich 0,99901. Dieses Ereignis ist also fast sicher. Die Wahrscheinlichkeit, bei einem ausgefüllten Lottofeld 6 Richtige zu erzielen, ist etwa gleich 0,00000007. Dieses Ereignis ist also fast unmöglich. Immerhin erhöht sich diese Wahrscheinlichkeit auf etwa 0,0000004, wenn sechs Lottofelder zufällig und unabhängig voneinander ausgefüllt werden.
Andererseits: In Deutschland leben derzeit insgesamt ungefähr 82 Millionen Menschen. Wenn man davon ausgeht, dass hiervon jeder Dritte Lotto spielt und dass jeder Lottospieler vier Lottofelder zufällig und unabhängig voneinander ausfüllt, dann ist die Wahrscheinlichkeit dafür, dass niemand in Deutschland 6 Lottorichtige hat, etwa gleich 0,0004. Das bedeutet, dass es ziemlich sicher ist, dass bei einem Lottospiel unter den genannten Voraussetzungen irgendjemand 6 Richtige erzielen wird.
Von guten und schlechten Vasen
Beim Brennen von Vasen im Handwerksbetrieb Vaselon erhält man
erfahrungsgemäß 40% Vasen erster Wahl, 50% Vasen zweiter Wahl und 10%
Ausschuss. Wenn zwei solcher Vasen gebrannt werden sollen und davon ausgegangen
werden darf, dass der Herstellungsprozess einer Vase den einer anderen nicht
beeinflusst, kann man diesen Brennprozess als 2-stufiges
Zufallsexperiment
auffassen. Mit welcher Wahrscheinlichkeit erhält man genau eine Vase
erster Wahl?
Ein mehrstufiges Zufallsexperiment lässt sich übersichtlich mit einem Baumdiagramm darstellen, im Falle der zwei zu brennenden Vasen sieht das etwa wie folgt aus:
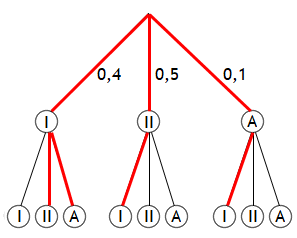
Jedes mögliche Ergebnis dieses Experimentes entspricht einem der Pfade im Baumdiagramm, es gilt also für die Ergebnismenge
S = { (I,I), (I,II), ..., (A,A) }.
Zum Ereignis "Genau eine Vase erster Wahl" gehören die Ergebnisse (I,II), (I,A), ... und damit die im Diagramm rot markierten Pfade. Mit dem Additionssatz zusammen mit dem Multiplikationssatz ergibt sich
P("Genau eine Vase erster Wahl")
= 0,4·0,6 + 0,5·0,4 + 0,1·0,4
= 0,48.
Das Nadelproblem von Buffon
Eine ebene Fläche sei mit äquidistanten Geraden durchzogen, wobei d, der
Abstand zweier benachbarter Parallelen, nicht zu groß gewählt werden darf.
Auf diese Fläche soll nun zufällig eine dünne Nadel mit der Länge l geworfen
werden. Wie groß ist − unter der Voraussetzung, dass l kleiner ist als d −
die Wahrscheinlichkeit, dass diese Nadel auf eine der Geraden trifft?
Dieses Problem wurde neben anderen wahrscheinlichkeitstheoretischen Fragen vom französischen Naturforscher Georges Louis Leclerc Comte de Buffon (1707-1788) im Jahr 1733 in einem Vortrag vor der Pariser Akademie der Wissenschaften behandelt. Mit Hilfe der Integralrechnung kann Buffon’s Problem wie folgt gelöst werden:
Wird der Abstand zwischen dem Mittelpunkt der geworfenen Nadel
und derjenigen Geraden, die der Nadel am nächsten liegt, mit x und der von
Nadel und Gerade eingeschlossene Winkel mit ξ bezeichnet,
so besteht die (unendliche) Ergebnismenge S dieses Zufallsexperimentes aus
allen Wertepaaren (ξ; x) mit 0 < ξ ≤ π
und 0 ≤ x ≤ d2.

Die geworfene Nadel schneidet oder berührt eine der Geraden genau dann,
wenn die Bedingung x ≤ l2·sin(ξ) erfüllt ist.
Deswegen entspricht dem Ereignis "Nadel trifft Gerade" die orangene Fläche A
im folgenden Diagramm; zur Ergebnismenge gehört die Fläche des Rechtecks mit der Länge π
und der Breite d2:
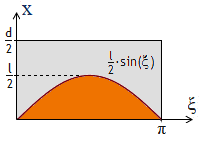
Geht man davon aus, dass es sich bei diesem Nadelexperiment um ein Laplace-Experiment handelt, dann gilt
P("Nadel trifft Gerade") = 2Aπ·d.
Wegen A = π∫0l2sin(ξ) dξ = l folgt
P("Nadel trifft Gerade") = 2 lπ d,
und damit ergibt sich die Möglichkeit, mit dem Buffon’schen Nadelexperiment die Kreiszahl π näherungsweise zu bestimmen bzw. die eben vorgestellte Theorie zu verifizieren. Ist r die relative Häufigkeit des Ereignisses "Nadel trifft Gerade", dann hat man:
π ≈ 2 lrd.
Das folgende (mit JavaScript realisierte) Programm simuliert das Nadelexperiment. Es wurde oben stillschweigend vorausgesetzt, dass die mit den parallelen Geraden durchfurchte Ebene nach oben, unten, links und rechts gleichermaßen unbegrenzt ist. Das Programm berücksichtigt dies (auf welche Weise das funktioniert, bemerkt man, wenn man nur wenige Nadeln nacheinander fallen lässt und beobachtet, was passiert). n ist die Anzahl der Nadeln, die nach dem Klicken auf „run“ nacheinander geworfen werden, Δt ist die Zeit in Millisekunden, die verstreicht, bevor die jeweils nächste Nadel fallen wird.
