Algorithmus
Ein Abakus besteht im Wesentlichen aus vertikal angeordneten Sprossen, auf denen verschiebbare Perlen befestigt sind. Beim chinesischen suan pan sitzen auf je einer Sprosse im oberen Bereich zwei Perlen; im unteren Bereich befinden sich auf jeder der Sprossen fünf Perlen. Ordnet man nun diese Perlen auf bestimmte Weise an, so lassen sich in eindeutiger Weise Zahlen darstellen. Die folgenden Beispiele zeigen, wie das geht:




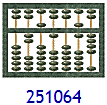
Zu jeder zulässigen Perlenanordnung gehört ein bestimmter Zahlenwert, wobei das dritte und das vierte Beispiel zeigen, dass die Umkehrung dieser Aussage nicht richtig ist. Wenn man alle Sprossenspalten von rechts nach links mit 0 bis 6 durchnummeriert, dann kann man mit einem solchen 7-sprossigen Abakus alle natürlichen Zahlen zwischen 0 und 16666665 darstellen und innerhalb dieses Zahlenraums addieren und subtrahieren, wenn folgende Regeln beachtet werden:
| Addieren von k·10i | Hochschieben von k unteren Kugeln in der i-ten Sprossenspalte |
| Subtrahieren von k·10i | Herunterschieben von k unteren Kugeln in der i-ten Sprossenspalte |
| Addieren von 5·10i | Herunterschieben einer oberen Kugel in der i-ten Sprossenspalte |
| Subtrahieren von 5·10i | Hochschieben einer oberen Kugel in der i-ten Sprossenspalte |
Normalerweise werden die Perlen eines Abakus mit Daumen und Zeigefinger verschoben. Bei dem hier mithilfe von JavaScript implementierten Abakus (→ Quelltext) muss man mit dem Mauszeiger die Perlen anklicken:
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||
| 0 |
Wahrscheinlich wurde der Abakus in dieser Form ein paar Jahrhunderte v. Chr. erfunden, nachdem zuvor beispielsweise mit Steinchen im Sand oder mit Stäbchen auf Rechenbrettern gerechnet wurde. Noch heute wird der Abakus als Rechenhilfsmittel vor allem in Asien verwendet. Selbst für das Multiplizieren und das Dividieren kann ein Abakus (mit genügend vielen Sprossen) gute Dienste leisten.
Man rechnet immer dann mit dem Abakus richtig, wenn zunächst durch entsprechendes Verschieben der Perlen die Eingangsdaten korrekt dargestellt werden, zweitens beim Bearbeiten der gestellten Rechenaufgabe die Regeln für das Verschieben der Perlen beachtet werden und drittens das Rechenergebnis vom Abakus fehlerfrei abgelesen wird.
Eine Folge von Anweisungen, nach denen man unter Vorgabe von Eingangsdaten eine bestimmte Ausgabe erhält, nennt man Algorithmus. Genauer:
Eine zur Lösung einer Klasse gleichartiger Probleme präzis formulierte Handlungsanweisung, die bei vorgegebenen Eingangsdaten eines festgelegten Typs mit Hilfe eindeutig definierter Regeln und unter Benutzung genau beschriebener Hilfsmittel unter Beachtung von Randbedingungen zu einem bestimmten Ergebnis führt, heißt Algorithmus.
Ein solcher Algorithmus, der zumeist aus einer Folge einzelner Anweisungen besteht, muss in einer Sprache verfasst sein, die der ausführende Mensch oder die ausführende Maschine verstehen und interpretieren kann.
Ein Algorithmus, der nach endlich vielen Schritten beendet ist, heißt terminierend. Wenn die Schrittfolge eines Algorithmus eindeutig festgelegt ist, so handelt es sich um einen deterministischen Algorithmus.
Ist das Ergebnis eines Algorithmus eindeutig bestimmt, so heißt dieser Algorithmus determiniert.
In der Grundschule lernt man, zwei Dezimalzahlen a und b miteinander schriftlich zu multiplizieren, und das geht so:

Dieses Multiplikationsverfahren funktioniert wegen der Rechenregeln bezüglich der Addition und der Multiplikation auf ℕ, der Menge der natürlichen Zahlen. Die erste vorgegebene Zahl a sei m-stellig, die zweite Zahl b sei n-stellig, das heißt a = a0·100 + a1·101 + ... + am−1·10m−1 und b = b0·100 + b1·101 + ... + bn−1·10n−1. Dann gilt
a·b = a·b0·100 + a·b1·101 + ... + a·bn−1·10n−1
Im Rechenbeispiel gilt a0 = 2; a1 = 8; a2 = 1; a3 = 4 bzw. b0 = 7; b1 = 3; b2 = 6 und es ist a·b0·100 = 29274; a·b1·101 = 12546 und a·b2·102 = 25092.
Jeder Summand a·bi·10i lässt sich für 0 ≤ i ≤ n−1 in die folgende Form bringen:
a·bi·10i = (bi·a0·100 + bi·a1·101 + ... + bi·am−1·10m−1)·10i
Im Rechenbeispiel sieht dies für i = 2 wie folgt aus:
4182·6·102 = (6·2·100 + 6·8·101 + 6·1·102 + 6·4·103)·102
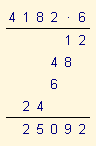
Die Aufgabe, eine m-stellige Dezimalzahl a mit einer n-stelligen Dezimalzahl b zu multiplizieren, erledigt man nach dem vorgestellten Verfahren durch n Multiplikationen der Zahl a mit 1-stelligen Dezimalzahlen, die den jeweiligen Ziffern der Zahl b entsprechen. Jede dieser n Multiplikationen führt dann zum richtigen Ergebnis, wenn man das kleine Einmaleins und das Addieren von 1-stelligen Dezimalzahlen unter Beachtung von Überträgen beherrscht. Der Wert von a·b ergibt sich schließlich durch Addition aller n Einzelergebnisse.
Für eine (mxn)Multiplikation einer m-stelligen Dezimalzahl a mit einer n-stelligen Dezimalzahl b benötigt man n (mx1)Multiplikationen mit jeweils höchstens 2m+1 elementaren Schritten (Multiplizieren bzw. Addieren zweier einstelliger Zahlen) und ungefähr m·n elementare Rechenschritte für das Addieren der n Einzelergebnisse, das sind insgesamt n·(2m+1) + m·n Schritte, also n·(3m+1) Schritte. Eine Verdoppelung der Ziffernanzahl beider Zahlen a und b ergibt demnach ungefähr eine Vervierfachung des Rechenaufwands bei der schriftlichen Multiplikation von a und b.
Der schottische Mathematiker Lord John Napier (1550−1617) hat ein Verfahren entwickelt, mit dem man unter anderem die Multiplikation einer m-stelligen Dezimalzahl mit einer 1-stelligen Dezimalzahl auf mechanische Art bewerkstelligen kann.
Auf den Napier’schen Rechenstäben sind untereinander Quadrate angeordnet, auf denen insgesamt alle Zahlen der Einmaleins-Reihen notiert sind, und zwar nach folgendem System:
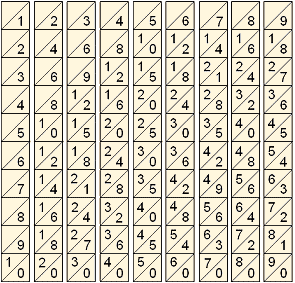
Die Funktionsweise des Napier’schen Multiplikationsverfahrens erschließt man sich am besten anhand eines Beispiels:
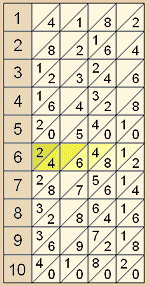 |
 |
Die Idee, Multiplikationen mithilfe diagonal
strukturierter Gittermuster durchzuführen, stammt nicht von Napier selbst,
sondern ist wesentlich älter. Zur Zeit Napiers war es üblich, zwei
mehrstellige Dezimalzahlen nach der vermutlich aus Indien stammenden Gelosia-Methode auf schriftlichem
Wege zu multiplizieren.
Ein Beispiel: 3716·297 = ?
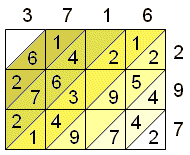
Die Ziffern des Produktwertes ergeben sich durch Addieren der entsprechenden Diagonalzahlen:
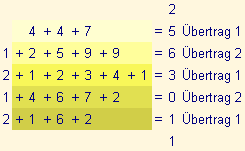
Das Endergebnis lautet: 1103652.
Unter Benutzung des Prinzips der Napier’schen Rechenstäbe hat Wilhelm Schickard (1592−1635), Professor für orientalische Sprachen und Astronomie an der Universität Tübingen, 1623 die erste mechanische Rechenmaschine konstruiert. Wesentlicher Bestandteil dieser Maschine war das Addierwerk, in das die Teilergebnisse der (mx1)Multiplikationen vom Benutzer der Maschine übertragen werden mussten.
Die Rechenmaschine von Schickard
![]()
Die von Schickard erdachte und vom Mechaniker Johann Pfister hergestellte Maschine kann wegen ihrer Funktionsweise durchaus als erster Computer der Welt bezeichnet werden: Nach der Eingabe von Daten (hier sind das die Ziffern zweier Dezimalzahlen) erfolgt - unter Mitarbeit des die Maschine bedienenden Menschen - die Verarbeitung dieser Daten im „Napier’schen Rechenwerk“; abschließend sieht man die Ausgabe des Rechenergebnisses. In einem Brief an Kepler schreibt Schickard:
aaa sind die Köpfchen senkrechter Zylinder, denen die Multiplikationen der Stellen einbeschrieben sind, die, soweit sie benötigt werden, durch die beweglichen Fenster bbb herausschauen. [Die Drehknöpfe] ddd haben innen befestigte zehnzähnige Rädchen, die so zusammengefügt sind, dass wenn irgendein rechtes sich zehnmal bewegt, das nächste linke einmal, oder wenn jenes 100 Umdrehungen macht, das dritte einmal usw. bewegt wird und zwar in derselben Richtung... Die jeweilige Zahl schaut durch die Öffnungen ccc in der mittleren Bank heraus. Auf der unteren Ebene schließlich bedeutet e Wirbel und f in ähnlicher Weise Öffnungen zur Darstellung von Zahlen, die während der Rechnung gebraucht werden.
Die Fensterchen bbb werden durch Bewegen der horizontal beweglichen Holzschieber (mit „2“ bis „9“ beschriftet) sichtbar.

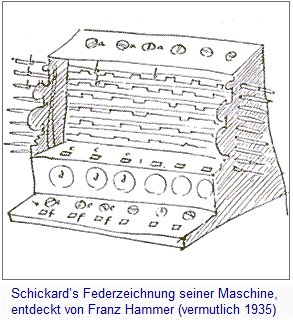
Die Abbildungen sind mit freundlicher Genehmigung von Herrn Prof.Setzler der folgenden Broschüre entnommen: Wilhelm Schickards Tübinger Rechenmaschine von 1623, Kleine Tübinger Schriften Heft 4, 2002, Kulturamt der Universitätsstadt Tübingen (Hrsg.).
Die folgende Simulation der Schickard’schen Maschine ist programmiert mit JavaScript.
|
|
a |
|
a |
|
a |
|
a |
|
a |
|
||||
| 0 | b |
0 | b |
0 | b |
0 | b |
0 | b |
0 | ||||
|
0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 |
|
|||||||
|
0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 |
|
|||||||
|
0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 |
|
|||||||
|
0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 |
|
|||||||
|
0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 |
|
|||||||
|
0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 |
|
|||||||
|
0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 |
|
|||||||
|
0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 |
|
|||||||
0 |
c | 0 |
c | 0 |
c | 0 |
c | 0 |
c | 0 |
||||
|
|
d |
|
d |
|
d |
|
d |
|
d |
|
||||
| 0 | f | 0 | f | 0 | f | 0 | f | 0 | f | 0 | ||||
|
|
e |
|
e |
|
e |
|
e |
|
e |
|
||||
Die Multiplikation zweier Dezimalzahlen mit der Schickard’schen Maschine funktioniert - sofern der Produktwert kleiner als 1000000 bleibt - folgendermaßen:
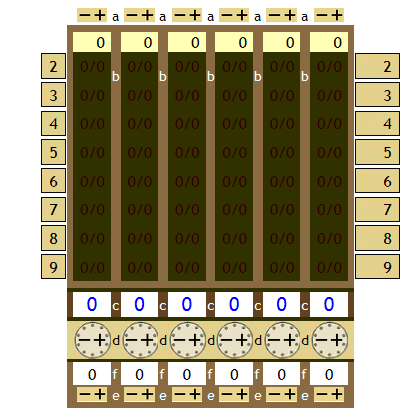
| Eingabe einer m-stelligen Zahl x | durch Drehen der Zylinderköpfchen aaa, hier: Mausklicks auf a |
| Eingabe einer n-stelligen Zahl y | durch Drehen der Wirbel eee, hier: Mausklicks auf e |
| Herausziehen des Schiebers, der der Einerziffer von y entspricht | hier: Mausklick auf den entsprechenden Schieber |
| Übertragen der „Napier'schen Zahlen" ins Addierwerk von rechts nach links ab dem Einerdrehknopf | durch Drehen der entsprechenden Knöpfe ddd, hier: Mausklicks auf d |
| Schließen aller geöffneten Fensterchen bbb | hier: Mausklick auf den entsprechenden Schieber |
| Herausziehen des Schiebers, der der Zehnerziffer von y entspricht | hier: Mausklick auf den entsprechenden Schieber |
| Übertragen der „Napier'schen Zahlen“ ins Addierwerk von rechts nach links ab dem Zehnerdrehknopf | durch Drehen der entsprechenden Knöpfe ddd, hier: Mausklicks auf d |
| u.s.w. | |
| Ablesen des Endergebnisses in den Fenstern ccc |
Ein Beispiel: 357 · 412 = ?
Der Schickard’sche Algorithmus zur Multiplikation zweier Dezimalzahlen ist aufgrund der nicht trivialen Bedienung der Drehknöpfe ddd zumindest für einen ungeübten Benutzer fehleranfällig. Die vollständig mechanische Bearbeitung von Grundrechenaufgaben war erst mit den sogenannten Vier-Spezies-Maschinen möglich. Die erste Rechenmaschine dieser Art wurde 1672 von Gottfried Wilhelm Leibniz (1646−1716) entwickelt. Wesentliche Bauteile waren die von Leibniz erfundenen Staffelwalzen. Erst ein Jahrhundert später gelang es dem schwäbischen Pfarrer Philipp Matthäus Hahn (1739−1790), die erste funktionstüchtige Staffelwalzenmaschine zu konstruieren.
Es gab im Laufe der Zeit noch Rechenmaschinen mit anderen
Konstruktionsprinzipien bis hin zur legendären Curta des Wiener
Rechenmaschinen-Fabrikanten Samuel Jacob Herzstark (1902−1988). Informationen hierzu gibt es zum Beispiel bei
Jan Meyer: Geschichte der
Rechenhilfsmittel![]() ,
W.G. Blümich:
Mechanische Rechenhilfsmittel
,
W.G. Blümich:
Mechanische Rechenhilfsmittel![]() und Harald
Schmid:
Facit-Rechenmaschinen
und Harald
Schmid:
Facit-Rechenmaschinen![]() .
.
Die Funktion aller mechanischen Rechenmaschinen beruht auf mathematisch begründbaren Rechenalgorithmen, die durch das planmäßige Ineinandergreifen mechanischer Bauteile realisiert wurden. Die Ziffern von Dezimalzahlen wurden dabei durch genau definierte Stellungen von Zahnrädern dargestellt.
Eine solche analoge Darstellung von Zahlen ist in
elektronischen Rechenmaschinen nicht möglich. Hier braucht man die
binäre Darstellung von Zahlen unter Benutzung von genau zwei
unterscheidbaren Zeichen.
Die binäre Darstellung einer natürlichen Zahl z ist zum Beispiel möglich,
indem man diese nicht - wie im Dezimalsystem - zur Basis 10 aufschreibt,
sondern zur Basis 2.
Mit Hilfe der Zweierpotenzen kann jede natürliche Zahl z ∈ ℕ wie folgt dargestellt werden:
z = z0·20 + z1·21 +...+ zn−1·2n−1.
Hierbei ist jedes der zi entweder die Zahl 0 oder die Zahl 1.
Dies lässt sich verallgemeinern:
Eine natürliche n-stellige Zahl z mit der Darstellung
z = z0·b0 + z1·b1 +...+ zn−1·bn−1
heißt Zahl zur Basis b. In abkürzender Schreibweise:
z = [zn-1...z2z1z0]b
Eine Zahl zur Basis 10 heißt Dezimalzahl, eine Zahl zur Basis 2 Dualzahl, eine Zahl zur Basis 8 Oktalzahl, eine Zahl zur Basis 16 Hexadezimalzahl.
Die im Ausdruck [zn-1...z2z1z0]b für die zi einsetzbaren Zahlzeichen heißen Ziffern des jeweiligen Stellenwertsystems. Zulässige Ziffern: 0 und 1 im Dualsystem; 0, 1, 2, 3, 4, 5, 6 und 7 im Oktalsystem; 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9 im Dezimalsystem; 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E und F im Hexadezimalsystem.
![]() Beispiel 1:
Beispiel 1:
Darstellung zweier Zahlen unter Verwendung verschiedener Basen:
3016
= 0·160 +
3·161
= 4810 = 1·24 + 1·25
=
1100002.
1A7F16
= F·160 + 7·161 + A·162 + 1·163
= 15·160 + 7·161 + 10·162 + 1·163
= 678310
![]() Beispiel 2:
Beispiel 2:
Kodieren von Farbwerten mithilfe von Hexadezimalzahlen:
| FF000016 | 00FF0016 | 0000FF16 |
| 00000016 | FFFFFF16 | FFF1D316 |
![]() Beispiel 3:
Beispiel 3:
Darstellung von Sexagesimalzahlen in der babylonischen Mathematik:
1·604 + 27·603 + 0·602 + 3·601 + 45
= ![]()
Man erkennt an diesem Beispiel, dass die Babylonier weder Ziffern (im heutigen Verständnis) noch ein Symbol für die Zahl Null verwendet haben. (→ Die babylonische Keilschrifttafel Plimpton 322)
Die automatische Umrechnung einer natürlichen Zahl zur Basis 10 in eine natürliche Zahl zu irgendeiner Basis b lässt sich mit dem folgenden hier in JavaScript implementierten Algorithmus bewerkstelligen:
// wandelt eine Dezimalzahl dnum
// in eine Zahl zur Basis b um
var z = dnum; // Integer
var bpot = b; // Integer
var code = 0; // Integer
var ziffer = ""; // String
var ergebnis = ""; // String
if ((dnum > 0) && (b > 1)) {
while (bpot <= z) bpot = bpot*b;
do {
bpot = bpot/b;
code = Math.floor (z/bpot);
a = String.fromCharCode(code+55);
b = String.fromCharCode(code+48);
ziffer = (code > 9) ? a : b;
ergebnis = ergebnis + ziffer;
z = z - code*bpot;
} while (bpot > 1);
return ergebnis;
}
else return ("nix")
}
Die einzugebende Zahl dnum darf nicht negativ und die Zahl b muss größer als 1 sein. Als Ziffern werden die in ihrer Reihenfolge eindeutig festgelegten Zeichen eines Teilbereichs der 8Bit-ASCII-Codetabelle verwendet: 0, 1, ... 9, A, B, ... Z. Insgesamt stehen also durch diese (willkürlich festgelegte) Einschränkung 36 Zeichen zur Verfügung, so dass b kleiner als 37 sein muss.
| decToAnyBase ( | , | ) | ||
| z | bpot | bpot <= z | code | ziffer | ergebnis | bpot > 1 | |
| 0 | 2005 | 16 | true | 0 | true |
Unter der Voraussetzung, dass dnum, b ∈∈ ℕ mit b > 1 und dnum ≥ 0, terminiert dieser Algorithmus immer und liefert stets ein eindeutiges und korrektes Ergebnis (→ kompletter Quelltext des Programms).
Wann ist ein Algorithmus korrekt?
![]()
Ein Algorithmus heißt genau dann korrekt, wenn er immer exakt das tut, was man von ihm erwartet. Die Korrektheit eines Algorithmus lässt sich in vielen Fällen sogar beweisen, zumindest dann, wenn er unter Verwendung einer passenden Programmiersprache auf imperative Weise implementiert ist ("decToAnyBase" ist zum Beispiel ein imperativ formulierter Algorithmus).
Eine imperative Programmierung ist vor allem gekennzeichnet durch die Hintereinanderausführung von Anweisungen und die Verwendung folgender elementarer Sprachstrukturen, die anhand des Beispiels "decToAnyBase" erläutert werden:
Die Eingabewerte werden der Funktion decToAnyBase
unter Verwendung der formalen Parameter dnum und b übergeben.
Als Ausgabewert liefert die Funktion decToAnyBase eine Zeichenkette zurück.
Der Begriff „Variable“
bedeutet hier etwas anderes als in der Mathematik. Salopp gesprochen ist
eine Variable im Sinne der Informatik so etwas wie ein Behälter für
Werte eines bestimmten Typs.
Beispielsweise ist bpot eine Variable vom Typ Integer; ziffer ist eine
Variable vom Typ String.
Beispiele für arithmetische Ausdrücke:
bpot/b,
Math.floor (z/bpot)
Beispiele für logische Ausdrücke:
(bpot <= z),
((dnum > 0) && (b > 1))
Beispiele für Zeichenketten:
"",
"nix"
Beispiele:
code = 0;
ziffer = "";
ziffer = String.fromCharCode(code + 55);
z = z - code*bpot;
Beispiele:
function, var, if, else,
do, while, return
Beispiel:
if ((dnum > 0) && (b > 1))
{ //tue etwas }
else return ("nix");
Bedeutung: Falls dnum größer als 0 ist und
b größer als
1 ist, dann tue etwas, sonst liefere "nix" zurück.
Beispiel:
while (bpot <= z) bpot = bpot*b;
Bedeutung: Solange bpot kleiner oder gleich z ist,
multipliziere den Wert der Variablen bpot mit b, ersetze den alten
Wert von bpot durch den Produktwert von bpot·b und wiederhole dies
alles.
Ein Algorithmus muss sowohl syntaktisch als auch semantisch korrekt sein.
Die Syntax beschreibt die Grammatik der Programmiersprache. Sie umfasst alle sprachlichen Regeln, denen ein in dieser Sprache geschriebener Programmquelltext genügen muss. Zur Formulierung dieser Regeln verwendet man üblicherweise Syntaxdiagramme oder den Backus-Naur-Formalismus.
Die Semantik betrifft den Sinn und die Bedeutung des Programmquelltextes. Ein syntaktisch korrekter Programmquelltext ist keineswegs automatisch auch semantisch korrekt. Beispielsweise ist die syntaktisch korrekte Programmierzeile
zahl = 3*feld[5]+1;
semantisch dann sinnlos, wenn die Arraykomponente feld[5] zuvor mit einer Zeichenkette belegt wurde und zahl der Bezeichner einer integer-Variablen ist (string und integer sind nicht miteinander verträgliche Datentypen!). Ein Programmquelltext ist insbesondere nur dann sinnvoll, wenn zum Beispiel bei Wertzuweisungen oder Vergleichen die dort verwendeten Datentypen zueinander passen.
Die im Allgemeinen schwierigste Aufgabe bei der Bewertung eines Algorithmus, der in Form eines Programmquelltextes vorliegt, ist es zu zeigen, dass dem syntaktisch korrekten und sinnvoll geschriebenen Algorithmus tatsächlich die Bedeutung zukommt, die vom Programmierer beabsichtigt war. Eine ganz andere Frage ist, ob ein gegebener Algorithmus unabhängig von der Wahl der (zulässigen) Eingabedaten immer terminiert. Schließlich ist noch sicherzustellen, dass die Maschine, die einen als korrekt erkannten Algorithmus schrittweise abarbeitet, auch fehlerfrei funktioniert.
Die von Alan Turing (1912−1954) entwickelte und nach ihm benannte Turing machine ist ein mathematisches Modell eines Universalrechners. Mit diesem Modell ist es möglich, Begriffe wie Algorithmus und Entscheidbarkeit formal zu präzisieren.
Die Turingmaschine besteht aus einem nach links und rechts unbeschränkt weit reichenden Band, das in sequentiell angeordnete Felder unterteilt ist („Turingband“). In jedes dieser Felder kann jeweils ein einzelnes Zeichen geschrieben werden; durch das Arbeitsalphabet Z wird definiert, welche Zeichen hierfür verwendet werden dürfen. In jedem Arbeitsschritt der Turingmaschine macht der Schreib-Lesekopf nacheinander die folgenden Dinge: 1. Er liest dasjenige Zeichen vom Turingband, das sich an der Position des Schreib-Lesekopfes befindet. 2. Er überschreibt dieses Zeichen entweder mit dem gleichen oder einem anderen Zeichen aus dem Arbeitsalphabet. 3. Er bewegt sich zu dem rechts- oder dem links-benachbarten Feld oder er bewegt sich garnicht. Zu Beginn kann ein (endlich langes) Eingabewort auf dem Turingband stehen; das Eingabealphabet legt fest, aus welchen Zeichen das Eingabewort bestehen darf. Alle nicht durch das Eingabewort belegten Felder sind anfangs mit einem Leerzeichen („_“) beschrieben. Für das Eingabealphabet E gilt:
E ⊆ Z \ { _ }.
Welches Zeichen im jeweiligen Arbeitsschritt auf das Turingband geschrieben wird, hängt vom aktuellen Zustand der Turingmaschine ab und wird definiert durch die Übergangsfunktion (Transitionsfunktion) τ:
τ: S x Z → S x Z x D mit D = {L, R, H}.
Hierbei bezeichnet Z die (endliche) Zustandsmenge der Turingmaschine und D beinhaltet die möglichen Bewegungsrichtungen: „L“ für „ein Schritt nach links“, „R“ für „ein Schritt nach rechts“, „H“ für „Halt“. Die Funktion τ wird üblicherweise durch eine Turingtabelle angegeben. Wenn in einer Zeile der Turingtabelle beispielsweise das 5-Tupel "1_02R" steht, dann bedeutet dies folgendes: Wird im Zustand s1 auf dem Turingband das Zeichen „_“ gelesen, so wird dieses mit dem Zeichen „0“ überschrieben, die Turingmaschine geht in den Zustand s2 über und der Schreib-Lesekopf bewegt sich einen Schritt nach rechts. Übergänge, die bei zulässigen Eingabeworten garnicht eintreten können, brauchen nicht unbedingt in der Turingtabelle berücksichtigt werden. (Man spricht dann von einer partiellen Übergangsfunktion.)
Zu Beginn befindet sich die Turingmaschine in einem bestimmten Anfangszustand, der Schreib-Lesekopf steht an der Position pos = 0; auf dem Turingband befindet sich dort das erste Zeichen des Eingabewortes.
Alles in allem wird durch eine Turingmaschine eine Funktion definiert, welche ein Eingabewort (welches durchaus eine beträchtliche Länge haben kann), auf eine Zeichenkette abbildet, die nach getaner Arbeit des Schreib-Lesekopfes auf dem Turingband steht. Voraussetzung ist hierbei erstens, dass das Ergebniswort nach endlich vielen Arbeitsschritten erreicht wird und dass zweitens für jede mögliche Konfiguration (gegeben durch die aktuelle Zeichenkette auf dem Turingband, den aktuellen Zustand der Maschine und der aktuellen Position des Schreib-Lesekopfes) ein Übergang in der Turingtabelle definiert ist.
Der folgende Emulator einer Turingmaschine ist mit JavaScript programmiert. Man kann mit den vordefinierten Turingprogrammen experimentieren, aber auch eigene Programme entwickeln und sie − sofern der verwendete Webbrowser dies unterstützt − im lokalen Speicher (localStorage) speichern.
| LOAD | |
Addieren zweier unärer Zahlen |
| LOAD | |
Verdoppeln einer unären Zahl |
| LOAD | |
Fleißiger Biber der Ordnung 4 |
| LOAD | |
Addieren zweier Dualzahlen |
| LOAD | |
Kopieren einer Zeichenkette (1) |
| LOAD | |
Kopieren einer Zeichenkette (2) |
Eine Funktion, die mit Hilfe einer Turingmaschine berechnet werden kann, wird turing-berechenbar genannt. Gemäss der Church-Turing-These, wonach die Klasse der turing-berechenbaren Funktionen mit der Klasse der intuitiv berechenbaren Funktionen übereinstimmt, kann es grundsätzlich keine Rechenmaschine geben, die rechenmächtiger ist als die Turingmaschine. Anders ausgedrückt: Alles, was überhaupt berechenbar ist, vermag auch die Turingmaschine zu berechnen und umgekehrt! Deswegen ist es möglich, die oben gegebene intuitive Algorithmusdefinition durch die folgende Definition zu ersetzen:
Ein Algorithmus ist ein Verfahren, das von einer Turingmaschine ausgeführt werden kann.
