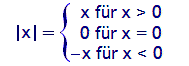Änderungsrate
 Sieht
ein Autofahrer dieses Verkehrsschild, dann heißt es
Aufpassen, denn die Straße steigt demnächst steil an. Genauer ausgedrückt: Der
Höhenunterschied beträgt 12 Meter bezogen auf 100 Meter in
horizontaler Richtung. Dies bedeutet, dass die Straße von der Seite
betrachtet so ausschaut:
Sieht
ein Autofahrer dieses Verkehrsschild, dann heißt es
Aufpassen, denn die Straße steigt demnächst steil an. Genauer ausgedrückt: Der
Höhenunterschied beträgt 12 Meter bezogen auf 100 Meter in
horizontaler Richtung. Dies bedeutet, dass die Straße von der Seite
betrachtet so ausschaut:
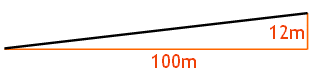
Anhand dieser Zeichnung erkennt man, dass - mathematisch gesehen - die Darstellung der ansteigenden Straße auf dem Verkehrsschild nicht korrekt ist. Die auf dem Schild dargestellte Steigung beträgt nämlich nicht nur 12100, sondern ungefähr 47, was rund 57% entspricht.

Bezeichnet man den Höhenunterschied mit ∆y und die in horizontaler Richtung zurückgelegte Strecke mit ∆x, dann gilt für die Steigung m:
m = ∆y∆x.
Das Verhältnis ∆y∆x gibt an, um wieviele Meter die Höhe bei konstant ansteigender Straße wächst, und zwar relativ zu ∆x. Bei der oben abgebildeten Straße ist m = 6m50m = 12100 = 12%.
Lässt sich die Abhängigkeit irgendeiner Größe y von einer anderen Größe x mithilfe einer Geraden beschreiben (man sagt dann: y hängt linear von x ab), dann gilt
y = m·x + c.
Der Steigungsfaktor m gibt an, wie stark
sich y in Abhängigkeit von x ändert:
Im folgenden Beispiel ist m = 47 und c = 2.
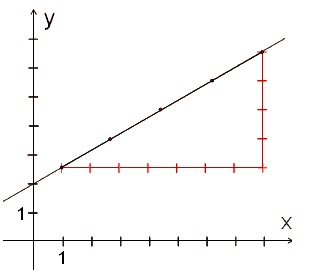
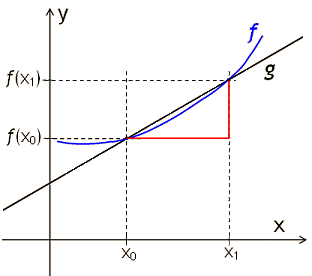
Der Begriff der Steigung lässt sich verallgemeinern:
Sei f eine auf [a, b] ⊂ ℝ
definierte Funktion.
x0,x1
∈∈ [a, b] mit
x0 < x1. Dann heißt
f(x1) − f(x0)x1 − x0
Änderungsrate (oder Differenzenquotient) von f im Intervall [x0, x1].
Diese Definition ist nur dann sinnvoll, wenn sich die Funktionswerte von f innerhalb des Intervalls [a, b] nirgendwo sprunghaft ändern. Mit anderen Worten: die Funktion muss stetig sein.
f(x1) − f(x0)x1 − x0 ist gleich der Steigung m der Geraden durch die Punkte (x0|f(x0) und (x1|f(x1). Durch diese Gerade wird eine lineare Funktion g definiert. Falls nun der Abstand zwischen x0 und x1 nicht zu groß ist, kann die Funktion f auf dem Intervall [x0, x1] durch die lineare Funktion g näherungsweise ersetzt werden. Diese Approximation ist um so besser, je kleiner (x1 − x0) gewählt wird.
Aus g(x0) = mx0 + c folgt
c = g(x0) − mx0.
Also gilt g(x) = mx + (g(x0) − mx0) = m·(x − x0) + g(x0) für x ∈∈ [x0, x1] und damit hat man
f(x) ≈ m·(x − x0) + f(x0) für x ∈∈ [x0, x1].
Für das zuletzt gezeichnete x-y-Diagramm kann man konkrete Interpretationen (er)finden. Beispielsweise lassen wir zwei Autos auf einer schnurgeraden Straße fahren, die zwei Fahrspuren hat. Beide Autos sollen zur selben Zeit x0 und an der gleichen Stelle y0 starten und später (zur Zeit x1) gleichzeitig an einer bestimmten Stelle y1 ankommen. Die folgende Zeichnung zeigt beide Autos von oben gesehen zur Startzeit.

Das blaue Auto fährt zunächst langsam los und wird dann immer schneller, das heißt, die Geschwindigkeit des blauen Autos nimmt während der Fahrt zu. Dagegen fährt das schwarze Auto während der gesamten Fahrt gleichförmig, das heißt, die Geschwindigkeit des schwarzen Autos bleibt durchgehend konstant.

Die Änderungsrate y1 − y0x1 − x0 liefert in diesem Beispiel sowohl den konstanten Wert der Geschwindigkeit des schwarzen Autos als auch den Wert der Durchschnittsgeschwindigkeit des blauen Autos auf der Fahrt von y0 nach y1. Diese Aussage bleibt auch dann richtig, wenn sich die Geschwindigkeit des blauen Autos zwischendurch sehr stark ändert. Wesentlich ist einzig und allein, dass beide Autos zusammen losfahren und zusammen ankommen.

Mit Hilfe der oben definierten Änderungsrate y1 − y0x1 − x0 kann man also in Bezug auf ein ausgewähltes Intervall [x0, x1] die durchschnittliche Änderung der Funktionswerte einer gegebenen Funktion bestimmen.
Sei irgendeine reellwertige Funktion f auf einem Intervall [a, b] ⊂ ℝ gegeben. Kann man das lokale Änderungsverhalten von f an beliebig gewählten Stellen x0 ∈∈ [a, b] berechnen? Mit anderen Worten: Gibt es eine Methode, momentane Änderungsraten von f an denjenigen Stellen zu bestimmen, wo f definiert ist?
Möglicherweise ist es besser verständlich, wenn diese Fragestellung physikalisch formuliert wird, so wie es Sir Isaac Newton (1643−1727) getan hat: Gegeben sei ein Körper, der sich nicht gleichförmig bewegt. Gibt es dann eine Methode, die momentane Geschwindigkeit des Körpers zu einem bestimmten Zeitpunkt t0 zu bestimmen?

Experimentell betrachtet ist die Sache leicht: Man nehme einen Zeitpunkt kurz vor t0 und einen Zeitpunkt kurz nach t0, messe die im Zeitintervall ∆t vom bewegten Körper zurückgelegte Strecke ∆s und hat dann mit
v = ∆s∆t
die gesuchte Geschwindigkeit zur Zeit t0, und zwar um so genauer, je kleiner ∆t gewählt wird. Dieses Messverfahren ist aber in seiner Genauigkeit begrenzt, denn man kann in der Praxis das Zeitintervall ∆t nicht beliebig klein wählen.
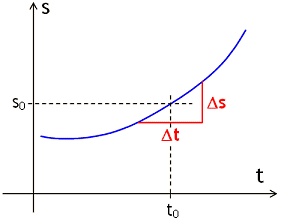
Kann der Prozess des Immer-kleiner-Werdens von ∆t bzw. von ∆s theoretisch weiter geführt werden mit dem Ziel, Momentangeschwindigkeiten nicht nur (mit einer unter Umständen kleinen, aber immer bestehenden Messungenauigkeit) zu messen, sondern (exakt) zu berechnen?
Für Gottfried Wilhelm Leibniz (1646−1716) war die Frage nach der Berechnung einer Momentangeschwindigkeit gleichbedeutend mit dem Problem, die Steigung der Tangente an einer t-s-Kurve im Punkt (t0|s0) zu bestimmen. Die nachfolgende Bildsequenz (die nur bei aktiviertem JavaScript funktioniert) zeigt auf anschauliche Weise, warum das Newton’sche Geschwindigkeitsproblem und das Leibniz’sche Tangentenproblem gleichwertig sind. Im hier dargestellten Beispiel gilt t0 = 1 und s0 = 1 (Einheiten müssen uns an dieser Stelle nicht interessieren).
Die Idee, das lokale Änderungsverhalten einer Funktion mit Hilfe eines solchen „Funktionenmikroskops“ zu untersuchen, stammt von Arnold Kirsch. Die sukzessive Vergrößerung des abgebildeten Funktionsgraphen um den Punkt (1|1) herum liefert bei genügend starker Vergrößerung fast die Tangente am Funktionsgraphen im Punkt (1|1)! Das Problem, die momentane Änderungsrate der hier gegebenen Funktion an der Stelle 1 zu bestimmen, läuft also anscheinend darauf hinaus, die Steigung der Tangente an dieser Stelle zu berechnen.
Doch der bloße Augenschein allein kann trügen! Dies zeigt das folgende Beispiel aufeinander folgender Treppenkurven, die allesamt die Länge 2 besitzen. Die Folge dieser Treppenkurve nähert sich augenscheinlich beliebig dicht der Quadratdiagonalen, deren Länge der Quadratwurzel aus 2 entspricht. Es gilt aber
![]()
Tangentensteigung und Differentialquotient
![]()
Sei eine Funktion f auf einem Intervall [a, b] ⊂ ℝ definiert und a < x0 < b. Wenn die Tangente an der durch y = f(x) definierten Kurve im Punkt P(x0|f(x0) in eindeutiger Weise existiert, dann gilt für die Steigung m dieser Tangente:
m =limx → x0
x ǂ x0
f(x) − f(x0)x − x0.
Hierbei ist Q(x1|f(x1) irgendein von P verschiedener Punkt auf dem Graphen von f. Die hier angegebene Formel besagt, dass die Tangentensteigung m, das heißt die „Steigung des Schaubildes der Funktion f an der Stelle x0“ um so genauer durch den Differenzenquotienten f(x1) − f(x0)x1 − x0 bestimmt werden kann, je näher der Punkt Q an P heranrückt.
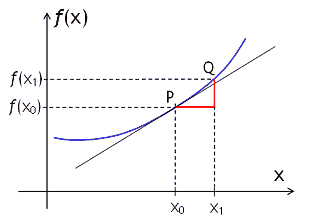
Anders ausgedrückt: Wenn x1 gegen x0 strebt, dann strebt der Differenzenquotient gegen die Tangentensteigung m. Für diesen Grenzwert, der Ableitung (oder Differentialquotient) der Funktion f an der Stelle x0 genannt wird, gibt es unterschiedliche Bezeichnungen. Heute wird meistens die erstmals von Joseph Louis Lagrange (1736−1813) vorgeschlagene Bezeichnung f’(x0) oder die von Augustin Louis Cauchy (1789−1857) eingeführte Bezeichnung Df(x0) verwendet. Leibniz benutzte für den Differentialquotienten die Abkürzung dydx (gesprochen: „dy nach dx“), die vor allem in der Physik sehr gebräuchlich ist.
Existiert die Ableitung der Funktion f an jeder Stelle x ∈∈ [a, b], kann man für alle diese x zusammenfassend schreiben:
dydx = df(x)dx = f’(x) = lim
h→0
f(x+h) − f(x)h.
Durch die Zuordnung x ↦ f’(x) für alle x ∈∈ [a, b] wird auf [a, b] die Funktion f’ definiert: die Ableitungsfunktion von f. Das Berechnen der Ableitung einer Funktion f nennt man Differenzieren von f.
Dies alles ist recht anschaulich und nachvollziehbar, doch das Ganze hat einen ganz beträchtlichen Haken: Die Begriffe „um so genauer“, „strebt gegen“, „beliebig klein“ (und so weiter) sind - so wie sie in diesem Abschnitt benutzt wurden - alles andere als präzise und definiert. Die Schlüsselbegriffe für die Präzisierung der mathematischen Grundlagen dieser Dinge in den nachfolgenden Abschnitten heißen Betrag und Folge.
Die Menge der reellen Zahlen ist mit der auf dieser Menge definierten Relation „≤“ linear geordnet. Das heißt, es gilt für alle x,y,z ∈∈ ℝ:
x ≤ y und
y ≤ z ⇒
x ≤ z
(Transitivität)
x ≤ y und
y ≤ x ⇒ x = y
(Identitivität)
x ≤ x
(Reflexivität)
x ≤ y oder y ≤ x
(Konnexität)
Im Falle dass x ≤ y und x ǂ y schreibt man x < y.
![]() B1
(Trichotomieeigenschaft der reellen Zahlen)
B1
(Trichotomieeigenschaft der reellen Zahlen)
Für zwei reelle Zahlen x und y gilt genau eine der drei
Beziehungen x < y, x = y, x > y.
Beweis:
Sei x,y ∈∈ ℝ.
Dann gilt entweder x ≤ y oder y ≤ x oder beides, also x = y.
Falls x ≤ y und x ǂ y folgt x < y; falls
y ≤ x und x ǂ y folgt
x > y.
Mit anderen Worten: Eine der drei Beziehungen gilt in jedem Fall.
Es ist noch zu zeigen, dass nur höchstens eine der drei Beziehungen gelten kann.
Mit x < y oder x > y folgt definitionsgemäß x ǂ y, das heißt es gilt nicht x = y.
Wenn also x = y gilt, dann gilt weder x < y noch x > y.
Sei nun x < y, das heißt x ≤ y und x ǂ y.
Angenommen, es gilt gleichzeitig auch y < x.
Aus der strengen Ungleichung y < x folgt die schwächere Aussage y ≤ x.
Aus x < y folgt ebenso x ≤ y.
Wegen der Identitivität in ℝ folgt x = y.
Widerspruch!
Aufgrund der Trichotomieeigenschaft der reellen Zahlen ist die folgende Definition sinnvoll:
Eine reelle Zahl x mit x > 0 heißt positiv. Ist x < 0, heißt x negativ.
Einige der für ℝ im Kapitel Zahlen bewiesenen Gesetze und Rechenregeln sollen zur besseren Übersicht hier zusammenfassend hingeschrieben werden:
Eigenschaften der reellen Zahlen
Die Eigenschaften G+, G·, D und N machen ℝ zu einem Körper.
Das Nullelement 0 und das Einselement 1 sind eindeutig bestimmt.
Das zu jedem x ∈∈ ℝ existierende x* mit x* + x = 0 ist eindeutig bestimmt und wird mit (−x) bezeichnet.
Für einen Ausdruck von der Form „x + (−y)“ verwendet man abkürzend die Schreibweise
„x − y“.
Das zu jedem x ∈∈ ℝ\{0} existierende x* mit x*·x = 1 ist eindeutig bestimmt und wird mit x−1 bezeichnet.
Aus x·y = 0 folgt x = 0 oder y = 0 (man sagt: ℝ ist nullteilerfrei).
Es gilt (−x) = (−1)·x
für alle x ∈∈ ℝ.
Hiermit folgt unter anderem: (−(xy)) = (−x)y, 0 = (−0)
und (−1)·(−1) = 1. (→ Beweis)
Für alle x,y,z ∈∈ ℝ
gilt
x > 0 und y > 0 ⇒
xy > 0 (→ Q9);
x < y ⇔ x + z < y + z (→ Q11).
ℝ ist im Gegensatz zu ℕ,
ℤ und ℚ
nicht abzählbar.(→ Q17)
|y − x| heißt Abstand zwischen x und y.
![]() B2
B2
Es gelten für alle x, y, x*, y*, z ∈∈ ℝ
folgende Regeln:
(U1) x < y ≤ z ⇒ x < z |
(U2) x ≤ y < z ⇒ x < z |
(U3) x ≤ x* und
y ≤ y* ⇒ x + y ≤ x* + y* |
(U4) x ≤ x* und
y < y* ⇒ x + y < x* + y* |
Beweis der ersten Aussage:
Sei x < y ≤ z. Dann gilt auch x ≤ y ≤ z.
Hieraus folgt wegen der Transitivität x ≤ z.
Angenommen, x = z. Dann folgt x ≤ y ≤ x und wegen der Identitivität hat man
x = y.
Nach Voraussetzung ist x < y und dies bedeutet x ǂ y.
Widerspruch! Es muss also x < z gelten.
Die zweite Aussage folgt auf analoge Art.
Beweis der dritten Aussage:
Es gilt x ≤ y ⇔ x + z ≤ y + z.
Aus x ≤ x* folgt demnach x + y ≤ x* + y.
Aus y ≤ y* folgt y + x* ≤ y* + x*.
In ℝ
gilt bezüglich „+“ das Kommutativgesetz. Also folgt die Behauptung.
Beweis der vierten Aussage:
Sei x ≤ x* und y < y*. Dann gilt auch x ≤ x* und y ≤ y*.
Es folgt x + y ≤ x* + y*.
Angenommen, x + y = x* + y*. Dann folgt
x* + y* = x + y ≤ x* + y ≤ x* + y*.
Wegen der Identitivität folgt x* + y* = x* + y und damit y = y*.
Nach Voraussetzung ist aber y < y*. Widerspruch!
Es folgt also x + y < x* + y* und damit die Behauptung.
![]() B3
B3
Eine reelle Zahl x ist genau dann positiv, wenn (−x)
negativ ist.
Ebenso ist
x genau dann negativ, wenn (−x) positiv ist.
Beweis:
zu zeigen: x > 0 ⇒ (−x) < 0.
Für eine positive reelle Zahl x gilt x > 0.
Für das Inverse dieser Zahl gilt in jedem Fall (−x) ≤ (−x).
Wegen (U4) folgt hieraus (−x) + 0 < (−x) + x.
Also gilt (−x) < 0, das heißt: (−x) ist negativ.
zu zeigen: (−x) < 0 ⇒
x > 0.
Sei (−x) eine negative reelle Zahl. Dann gilt (−x) < 0.
Mit (U4) folgt 0 = x + (−x) < x + 0
und damit x > 0.
![]() B4
B4
Für alle x ∈∈ ℝ
gilt
|x| ≥ 0.
Beweis:
x = |x| für x
≥ 0. Also gilt in diesem Fall auch |x| ≥ 0.
Wenn x negativ ist, dann ist (−x) und nach Definition
des Absolutbetrages auch |x| positiv.
Üblicherweise schreibt man für das Negative einer reellen Zahl statt (−x) nur −x.
![]() B5
B5
Sei ε eine positive reelle Zahl. Dann gilt für alle x ∈∈ ℝ
|x| ≤ ε ⇔ −ε ≤ x ≤ ε.
Beweis:
„⇒“:
Sei |x| ≤ ε.
Fall 1: x = |x|. Dann folgt x ≤ ε. Wegen ε > 0
gilt −ε < 0 ≤ |x| und damit −ε ≤ x.
Fall 2: x = −|x|. Dann folgt −x ≤ ε und somit −ε ≤ x. Wegen x = −|x|
ist x ≤ 0. Also gilt x ≤ ε.
Insgesamt folgt also in jedem Fall −ε ≤ x ≤ ε.
„⇐“: Sei −ε ≤
x
≤ ε. Dann folgt |x| ≤ ε sowohl für x = |x| als auch für x = −|x| unmittelbar.
Aus dem vorstehenden Satz folgt auch
|x| < ε ⇔ −ε < x < ε.
![]() B6
B6
Für alle x, y ∈∈ ℝ gilt
|xy| = |x|·|y| und
|x + y| ≤ |x| + |y|.
Beweis der ersten Aussage:
Zunächst sei bemerkt, dass x = −y und y = −x zwei zueinander
äquivalente Aussagen sind.
Es gilt x = |x| oder x = −|x|, bzw. y = |y|
oder y = −|y|.
Also gilt xy = |x|·|y| oder xy = −|x|·|y|.
Im ersten Fall ist xy
≥ 0 und diesem Fall gilt |xy| = xy.
Im zweiten Fall ist xy ≤ 0 und man hat |xy| = −xy = |x|·|y|.
Beweis der zweiten Aussage:
Für x = 0 oder y = 0 ist die Ungleichung offensichtlich wahr.
Unter der Voraussetzung, dass sowohl x als auch y von 0 verschieden sind,
gilt |x| + |y| > 0.
Hieraus folgt
−(|x|+|y|) ≤ x+y ≤ |x|+|y| und damit |x+y| ≤ |x|+|y|.
Eine Funktion f: ℕ → ℝ nennt man eine Zahlenfolge. Das n-te Folgenglied einer solchen Zahlenfolge wird mit „xn“, die gesamte Folge mit „(xn)“ oder genauer mit „(xn)n=0..∞“ bezeichnet.
Eine Folge reeller Zahlen (xn) heißt Cauchyfolge, falls Folgendes gilt:
Zu jedem positiven ε ∈∈ ℝ
existiert ein N ∈∈ ℕ, so dass gilt:
|xm − xn)| < ε für alle m, n ≥ N.
Eine Folge reeller Zahlen (xn) heißt konvergent, falls es eine Zahl x ∈∈ ℝ gibt, so dass (xn − x) eine Nullfolge ist, das heißt: zu jeder positiven Zahl ε ∈∈ ℝ gibt es ein N ∈∈ ℕ, so dass
|xn − x)| < ε für alle n ≥ N.
x heißt Grenzwert der Folge (xn) und man schreibt abkürzend
xn → x (n → ∞)
oder auch
lim n→∞xn = x.
![]() F1
F1
Der Grenzwert einer konvergenten Zahlenfolge ist stets eindeutig bestimmt.
Beweis:
Angenommen, eine konvergente Zahlenfolge (xn) hat
zwei voneinander verschiedene Grenzwerte x und y.
Dann gilt
|x − y|
= |(x − xn) + (xn − y)|
≤ |x − xn| + |xn − y|
→ 0 (n → ∞).
Also folgt x = y. Widerspruch zur Annahme!
Das Cauchy’sche Konvergenzkriterium besagt, dass eine reelle Zahlenfolge (xn) genau dann konvergent ist,
wenn sie eine Cauchyfolge ist (→ Beweis). Damit
wird die Menge der reellen Zahlen zu einem vollständigen metrischen Raum.
Ein metrischer Raum (M, d) heißt vollständig, wenn es zu jeder Cauchyfolge (xn) in M ein x ∈∈ M gibt, so dass (xn) gegen x konvergiert.
![]() F2 (Grenzwertsätze für Folgen)
F2 (Grenzwertsätze für Folgen)
Seien (xn) und (yn) zwei konvergente Zahlenfolgen mit xn → x und yn → y (n → ∞).
Dann sind auch die Folgen (xn + yn) und (xn·yn)
konvergent und es gilt
(i) (xn + yn)
→ x + y (n
→ ∞)
(ii)
(xn·yn) → x·y (n →
∞).
Falls xn ǂ 0 für alle n ∈∈ ℕ und x ǂ 0, so ist auch die Folge (1/xn) konvergent und es gilt
(iii) (1xn) → 1x (n → ∞).
Nimmt man in (ii) für (xn) die konstante Folge (cn) = c, c, c, ..., welche trivialerweise gegen c konvergiert, dann folgt sofort die Konvergenz der Folge (c·yn) und es ist
(iv) (c·yn) → c·y (n → ∞).
Setzt man c = −1, dann folgt aus (iv) zusammen mit (i) noch
(v) (xn − yn) → x − y (n → ∞).
Beweis der ersten Aussage:
Seien (xn) und (yn) konvergent mit xn → x und yn → y (n → ∞).
Dann gibt es zu jedem ε2 > 0 ein Nx ∈∈ ℕ bzw. ein Ny ∈∈ ℕ,
so dass
|xn − x| < ε2
für alle n ≥ Nx
und |yn − y| < ε2
für alle n ≥ Ny.
Also gilt für alle n ≥ max(Nx, Ny)
|(xn + yn) − (y + x)|
= |(xn − x) + (yn − y)|
≤ |xn − x| + |yn − y|
≤ ε2 + ε2 = ε,
was zu beweisen war.
Beweis der zweiten Aussage:
Seien (xn) und (yn) konvergent mit xn → x und yn → y (n → ∞).
Für alle n ∈∈ ℕ gilt
xn·yn − x·y
= xn·yn
− x·yn + x·yn − x·y
= (xn − x)·yn
+ x·(yn − y).
Die Folge (yn) ist konvergent und damit beschränkt.
Es lässt sich also eine reelle Zahl s finden mit |yn| < s
für
alle n ∈∈ ℕ und |x| < s.
Hieraus folgt unter Benutzung der Dreiecksungleichung für jedes n ∈∈ ℕ:
|xn·yn − x·y| ≤ |xn − x|·s + |yn − y|·s.
Nach Voraussetzung gibt es zwei natürliche Zahlen Nx und Ny,
so dass Folgendes gilt:
|xn − x| < ε2s
für alle n ≥ Nx
und |yn − y| < ε2s
für alle n ≥ Ny,
wobei die positive reelle Zahl ε beliebig gewählt werden kann.
Sei N = max(N, Ny), dann folgt
|xn·yn − x·y| ≤ s·ε2s + s·ε2s = ε für alle n ≥ N.
Beweis der dritten Aussage:
Sei (xn) konvergent mit xn → x
(n → ∞), wobei x ǂ 0 und xn ǂ 0 für alle
n ∈∈ ℕ.
Dann gibt es ein N, so dass
||xn|−|x|| ≤ |xn − x| < |x|2 für alle n ≥ N.
Die Ungleichung ||xn|−|x|| < |x|2 ist äquivalent zu der Aussage
−|x|2 < |xn|−|x| < |x|2.
Insbesondere folgt hieraus, dass |xn| > |x| −|x|2, also hat man |xn| > |x|2
für alle n ≥ N. Hiermit ergibt sich
|1xn − 1x| = |x − xn||xn|·|x| ≤ 2·|x − xn||x|2.
Sei nun ε > 0 beliebig gewählt. Dann gibt es ein N*, so dass für alle n ≥ N* gilt:
|x − xn| < min(|x|2, |x|2·ε2).
Damit hat man für alle n ≥ N*
|1xn − 1x| < |x|2·ε|x|2 = ε.
Der Begriff der Konvergenz einer Folge wird möglicherweise etwas anschaulicher mithilfe der Begriffe Umgebung und Häufungswert.
Sei ε eine positive reelle Zahl und x0 ∈∈ ℝ. Dann heißt die Menge
Uε(x0) = { x ∈∈ ℝ: |x − x0| < ε }
ε-Umgebung von x0.
Eine Menge U ⊂ ℝ heißt Umgebung von x0 ∈∈ ℝ, wenn U eine ε−Umgebung von x0 enthält. Man schreibt dann: U = U(x0).
x0 ∈∈ ℝ heißt Häufungswert (oder Häufungsstelle) der Menge M ⊂ ℝ, wenn in jeder Umgebung U(x0) unendlich viele Elemente von M liegen. x0 ∈∈ ℝ heißt Häufungswert der Zahlenfolge (xn), wenn in jeder Umgebung von x0 unendlich viele Folgenglieder dieser Folge liegen.
![]() F3
F3
Die Zahlenfolge (xn) konvergiert genau dann gegen x,
wenn in jeder Umgebung von x fast alle Glieder der Folge liegen, das
heißt: alle Folgenglieder mit höchstens endlich vielen Ausnahmen.
Beweis:
„⇒“: Sei (xn) eine konvergente
Folge mit xn → x (n → ∞) und U irgendeine Umgebung von x.
U(x) enthält nach Definition eine ε−Umgebung von x.
Für dieses ε gilt |xn − x)| < ε für alle n ≥ N
mit passend gewähltem N ∈∈ ℕ.
Damit hat man xn ∈∈ U(x)
für alle n ≥ N,
und nur höchstens n Ausnahmen liegen nicht in U(x).
„⇐“: x ∈∈ ℝ habe die Eigenschaft, dass in jeder Umgebung U(x) fast alle
Folgenglieder der Folge (xn) liegen.
Sei nun ε eine beliebige positive reelle Zahl.
Dann gibt es höchstens endlich viele xn, die außerhalb von Uε(x)
liegen. Diese Folgenglieder seien mit xm1, xm2, ..., xmt
bezeichnet. Für jedes n ∈∈ ℕ gilt dann
|xn| ≤ max(|x|+ε, |xm1|, |xm2|, ..., |xmt|).
Also ist die Zahlenfolge (xn) beschränkt.
Nach Voraussetzung ist x ein Häufungswert von (xn).
Angenommen, es gibt einen zweiten Häufungswert y von (xn)
mit y ǂ x,
dann ist d = |y − x| > 0 und für zwei ε-Umgebungen
Uε(x) und Uε(y) gilt
Uε(x) ∩ Uε(y) = { },
wenn
ε < d2 gewählt wird.
Damit liegen in Uε(x) nicht mehr fast alle Folgenglieder von (xn).
Widerspruch!
Die Folge (xn) ist somit beschränkt und hat nur einen einzigen Häufungswert, also konvergiert (xn) gegen x.
Aus F3 folgt unmittelbar
![]() F4
F4
Jede Teilfolge einer gegen x konvergenten Zahlenfolge (xn) ist ebenfalls konvergent und
strebt auch gegen x.
Wegen Q14 ist die Folge (1n)n∈∈ℕ* eine Nullfolge. Also ist 0 nach F3 Häufungswert von (1n) und zudem auch Häufungswert der Menge { 1n: n ∈∈ ℕ* }. Ein Häufungswert einer Folge (xn) muss nicht zwingend auch Häufungswert der zugehörigen Menge { xn } sein, was das Beispiel xn = (−1)n zeigt: Die so definierte Folge hat die zwei Häufungswerte 1 und −1, die zweielementige Menge { 1, −1 } hat natürlich keinen Häufungswert.
Nach dem fundamentalen Satz von Bolzano-Weierstraß (→ Beweis) enthält jede beschränkte reelle Zahlenfolge mindestens eine konvergente Teilfolge. Ist eine reelle Zahlenfolge (xn) beschränkt, so besitzt diese demnach mindestens einen Häufungswert. Enthält (xn) mehrere Häufungswerte, so heißt der größte unter ihnen Limes superior (in Zeichen: „lim sup xn“ oder „lim xn“), der kleinste Limes inferior (in Zeichen: „lim inf xn“ oder „lim xn“).
Es gilt also
![]() F5
F5
Eine Zahlenfolge (xn) ist genau dann konvergent,
wenn sie beschränkt ist und genau einen Häufungswert hat. Dieser
Häufungswert ist dann notwendigerweise der Grenzwert dieser Folge.
Stetigkeit und Differenzierbarkeit
![]()
Sei M ⊂ ℝ, x0 ein Häufungswert von M und f eine auf M definierte reellwertige Funktion. Ferner gebe es ein g ∈∈ ℝ, so dass für alle ε > 0 ein δ = δ(ε) > 0 existiert mit
|x − x0| < δ ⇒ |f(x) − g| < ε.
In diesem Fall schreibt man
f(x) → g (x → x0)
oder
lim x→x0f(x) = g
und sagt: „f(x) konvergiert gegen g für x gegen x0“.
![]() D1
D1
Sei M ⊂ ℝ und x0 ein
Häufungswert
von M, g ∈∈ ℝ
und f eine auf M definierte reellwertige Funktion.
Dann konvergiert f(x) genau dann gegen g für x gegen x0,
wenn für jede Zahlenfolge (xn), die gegen x0
konvergiert, die Folge (f(xn)) gegen g strebt.
Beweis:
„⇒“: Es sei f(x) → g (x → x0) und (xn) sei irgendeine Zahlenfolge mit xn → x0 (n → ∞).
Sei ε > 0 beliebig vorgegeben.
Dann existiert wegen der Konvergenz von f(x) ein δ = δ(ε) > 0
mit
|f(x) − g| < ε für alle x mit |x − x0| < δ.
Wegen xn → x0 (n → ∞)
gibt es eine von δ abhängige natürliche Zahl n0 mit
|xn − x0| < δ für alle n
mit n ≥ n0.
Also gilt |f(xn) − g| < ε für n ≥
n0 und damit hat man f(xn) → g (n → ∞).
„⇐“: Es gelte nun f(xn) → g
(n → ∞) für
jede Folge (xn), die gegen x0 konvergiert.
Angenommen, es gilt nicht f(x) → g (x → x0).
Dann gibt es ein ε > 0, so dass zu jedem δ > 0 ein x(δ) ∈∈ M existiert
mit
|x(δ) − x0| < δ und |f(x(δ)) − g| ≥ ε.
Mit δ = 1n hat man |x(1/n) − x0| < 1n. Hieraus folgt
x(1/n) → x0 (n → ∞)
und nach Voraussetzung gilt dann auch
f(x(1/n)) → g (n → ∞) .
Die Konvergenz von (f(x(1/n))) bedeutet nach Definition, dass
|f(x(1/n)) − g| < ε
ab einer bestimmten Indexzahl n. Dies steht im Widerspruch zur Ungleichung
|f(x(1/n)) − g| ≥ ε für n = 1, 2, 3, ...
Sei M ⊂ ℝ, x0 ∈∈ M und f eine auf M definierte reellwertige Funktion.
Dann heißt f stetig in x0, wenn es zu jedem
ε > 0 ein δ = δ(ε) > 0 gibt mit
|x − x0| < δ ⇒ |f(x) − f(x0)| < ε.
f heißt stetig auf M, wenn f stetig in x für alle x ∈∈ M ist.
Es sei hier bemerkt, dass Bernard Bolzano (1781−1848) bereits 1817 die Stetigkeit einer Funktion beschrieben hat, und zwar so: „Man versteht unter der Redensart, daß eine Function fx für alle Werthe von x, die inner- oder außerhalb gewisser Grenzen liegen, nach dem Gesetze der Stetigkeit sich ändre, nur so viel, daß, wenn x irgend ein solcher Werth ist, der Unterschied f(x+ω) − fx kleiner als jede gegebene Größe gemacht werden könne, wenn man ω so klein, als man nur immer will, annehmen kann.“
Sei M ⊂ ℝ, x0 ein Häufungswert von M und f eine auf M definierte reellwertige Funktion. Dann ist f offenbar genau dann stetig in x0, wenn f(x) → f(x0) (x → x0).
Mit dem eben bewiesenen Satz folgt unmittelbar
![]() D2 (Folgenkriterium)
D2 (Folgenkriterium)
Sei M ⊂ ℝ und f eine auf M
definierte reellwertige Funktion. Dann ist f in x0 ∈∈ M
genau dann stetig, wenn für jede Folge von Zahlen aus M,
die gegen x0 konvergiert, auch die Folge (f(xn))
gegen f(x0) konvergiert, das heißt, wenn für alle Folgen (xn)
lim n→∞f(xn) = f (lim n→∞xn )
gilt.
Die konstante Funktion fc und die Funktion fx, definiert durch fx(x) = x für alle x ∈∈ ℝ, sind nach dem Folgenkriterium trivialerweise stetig.
![]() D3
D3
Die Summe, die Differenz und das Produkt zweier stetiger Funktionen sind
wieder stetig. Der Quotient zweier stetiger Funktionen ist überall dort
stetig, wo der Nenner verschieden von 0 ist.
Beweis:
Die Aussagen folgen sofort aus dem Folgenkriterium in Verbindung mit den
Grenzwertsätzen.
Ein Term der Art
an·xn + an−1·xn−1 + ... + a1·x + a0
mit den Koeffizienten ak ∈∈ ℝ, k = 0, 1, 2, ..., n und an ǂ 0 heißt Polynom vom Grad n, kurz geschrieben:
n∑k = 0ak·xk.
Eine Funktion f, definiert durch
f(x) = n∑k = 0ak·xk für alle x ∈∈ ℝ,
wird ganzrationale Funktion (oder Polynomfunktion) genannt.
Aufgrund der Stetigkeit von fc und fx folgt mit D3 unmittelbar
![]() D4
D4
Ganzrationale Funktionen sind auf ganz ℝ
stetig.
![]() D5 (Satz vom Minimum und Maximum)
D5 (Satz vom Minimum und Maximum)
Sei f eine auf dem abgeschlossenen Intervall [a, b] definierte
Funktion. Wenn f auf [a, b] stetig ist, so besitzt f dort
einen größten und einen kleinsten Wert.
Beweis:
Angenommen, der Wertebereich
W
einer auf [a, b] definierten und dort stetigen Funktion f ist
nicht nach oben beschränkt. Dann gibt es innerhalb von [a, b] eine Folge (xn),
so dass (f(xn)), die Folge der zugehörigen
Funktionswerte, unbeschränkt wächst. Mit dem Satz von Bolzano-Weierstraß
folgt die Existenz einer Häufungsstelle x* von (xn).
In jeder noch so kleinen Umgebung von x* ∈∈ [a, b]
befinden sich also gewisse Folgenglieder xk der Folge (xn)
mit der Eigenschaft, dass |f(xk) − f(x*)|
beliebig groß wird. Das aber bedeutet die Unstetigkeit von f an der
Stelle x*, ein Widerspruch zur Voraussetzung.
Demnach ist f also nach oben beschränkt, womit W nach Q28 eine obere Grenze besitzt. Im Fall, dass sup W ∈∈ W, ist nichts mehr zu zeigen, denn dann ist sup W der größte Funktionswert von f auf [a, b].
Wenn sup W kein Element von W ist, so muss sup W ein Häufungswert von W sein. Das bedeutet, dass es dann innerhalb von [a, b] eine Folge (xn) gibt, so dass
lim n→∞f(xn) = sup
W
gilt. Aufgrund der Beschränktheit von (xn) besitzt diese Folge eine konvergente Teilfolge, etwa (tk)
mitlim k→∞tk = g.
Da in jeder Umgebung von sup W fast alle Folgenglieder der
Folge (f(xn)) liegen, trifft dies erst recht für fast
alle f(tk) zu. Demzufolge gilt
lim k→∞f(tk) = sup
W.
Andererseits ergibt sich aufgrund der Stetigkeit von f auf [a, b] wegen g ∈∈ [a, b] mit dem Folgenkriterium
lim k→∞f(tk) = f(g).
Hieraus folgt sup W = f(g) und damit der erste Teil der Behauptung. Der zweite Teil kann auf analoge Art bewiesen werden.
Das Folgenkriterium ermöglicht in Verbindung mit dem überaus nützlichen Instrument der Intervallschachtelung den folgenden wichtigen Satz zu beweisen:
![]() D6 (Nullstellensatz von Bolzano)
D6 (Nullstellensatz von Bolzano)
Ist eine reellwertige Funktion f auf einem abgeschlossenen Intervall
[a, b] ⊂ ℝ
definiert und dort überall stetig, und haben f(a) und f(b)
verschiedene Vorzeichen, dann existiert mindestens ein n ∈∈ ]a, b[ mit
f(n) = 0.
Beweis:
Sei f eine auf
[a, b] ⊂ ℝ
definierte und auf ]a, b[ überall stetige Funktion;
sei ferner ohne Beschränkung der Allgemeinheit f(a) < 0 und f(b) > 0.
Wir definieren nun induktiv eine Folge von Intervallen ([an, bn])n∈ℕ
wie folgt:
Sei zunächst a0 = a und b0 = b.
Angenommen, [ak, bk] sei bereits definiert für k ∈∈ ℕ,
dann sind für die Intervallmitte mk = ak + bk2
genau zwei Fälle zu unterscheiden:
Fall 1: f(mk) ≥ 0, dann sei
[ak+1, bk+1] = [ak, mk];
Fall 2: f(mk) < 0, dann sei [ak+1, bk+1]
= [mk, bk].
Für die so definierte Intervallfolge gilt:
Die Folge (an)n∈ℕ
ist monoton wachsend, d.h. a0 ≤ a1 ≤ a2 ≤
...
Die Folge (bn)n∈ℕ
ist monoton fallend, d.h. b0 ≥ b1 ≥ b2 ≥
...
Es gilt
an < bn für alle n ∈∈ ℕ.
bn − an = (b − a)·2−n →
0 für n → ∞,
das heißt, (bn − an)n∈ℕ
ist eine Nullfolge.
Damit ist ([an, bn])n∈ℕ eine Intervallschachtelung und die Folgen (an) und (bn) sind konvergent. Sei p der (gemäß Q26 eindeutig bestimmte) innere Punkt dieser Intervallschachtelung, dann ist p der gemeinsame Grenzwert der beiden Folgen (an) und (bn) für n → ∞.
Nun gilt entweder für mindestens ein n ∈∈ ℕ* f(bn) = 0, dann ist nichts mehr zu beweisen, oder es gilt f(bn) ǂ 0 für alle n ∈∈ ℕ*. Im letzteren Fall folgt wegen der Stetigkeit von f mit dem Folgenkriterium, dass die Folgen (f(an)) und (f(bn)) auch einen gemeinsamen Grenzwert für n → ∞ haben, nämlich f(p).
Mit f(an) ≤ 0 und f(bn) ≥ 0 für alle n ∈∈ ℕ folgt f(p) = 0, wie zu beweisen war.
Es ist leicht einzusehen, dass der eben bewiesene Nullstellensatz äquivalent ist zum Zwischenwertsatz:
![]() D7 (Zwischenwertsatz)
D7 (Zwischenwertsatz)
Ist eine reellwertige Funktion f auf einem abgeschlossenen Intervall
[a, b] ⊂ ℝ
definiert und dort überall stetig, ist ferner m irgendein
Wert zwischen f(a) und f(b), so nimmt
f den Wert m in dem Intervall mindestens einmal an.
Eine Menge M ⊂ ℝ heißt zulässig, wenn jedes x ∈∈ M Häufungswert von M ist.
Sei nun f eine auf einer zulässigen Menge M definierte
reellwertige Funktion und x0 ∈∈ M.
f heißt differenzierbar in x0, wenn es auf M eine
Funktion Δ gibt mit folgenden Eigenschaften:
| (D1) | Δ ist in x0 stetig. |
| (D2) | f(x) = f(x0) + (x−x0)·Δ(x) für x∈∈M. |
f heißt differenzierbar auf M, wenn für alle x ∈∈ M f differenzierbar in x ist.
Die Funktion Δ ist durch die Bedingungen (D1) und (D2) eindeutig bestimmt.
Beweis:
Es seien Δ1 und Δ2 zwei auf M ⊂ ℝ
definierte Funktionen mit den Eigenschaften (D1) und (D2).
Für jedes x ∈ M folgt dann (x − x0)·(Δ1(x) − Δ2(x)) = 0 wegen (D2).
Es gilt also Δ1(x) = Δ2(x) für alle x,
die verschieden sind von x0.
M ist zulässig und Δ ist in x0 stetig, also folgt auch Δ1(x0) = Δ2(x0).
Damit hat man Δ1(x) = Δ2(x) für alle x ∈∈ M.
Der Funktionswert Δ(x0) heißt Ableitung (oder Differentialquotient) von f in x0 und wird mit „f’(x0)“ bezeichnet. Vor allem in der Physik ist auch die Bezeichnung „dfdx(x0)“ üblich.
Ist eine Funktion f auf ganz M differenzierbar, dann heißt die auf M definierte Funktion f’, die jedem x ∈∈ M die Ableitung von f in x zuordnet, Ableitungsfunktion von f auf M (oder kurz: Ableitung von f).
Eine Funktion Δ, die nur die Eigenschaft (D2) hat, lässt sich immer finden. Das heißt, dass im Hinblick auf die Differenzierbarkeit einer Funktion f in x0 die Stetigkeit von Δ in x0 die wesentliche Forderung ist! So wie die Stetigkeit ist auch die Differenzierbarkeit von f eine lokale Eigenschaft. Stimmen zwei Funktionen f1 und f2 in einer Umgebung von x0 überein, so ist entweder keine der beiden in x0 differenzierbar oder aber beide sind dort differenzierbar und es gilt f1’(x0) = f2’(x0).
Falls eine Funktion Δ mit den Eigenschaften (D1) und (D2) existiert, so konvergiert der Differenzenquotient
Δ(x) = f(x) − f(x0)x − x0 mit x ǂ x0
wegen der Stetigkeit von Δ in x0 aufgrund des Folgenkriteriums gegen f’(x0), wenn x gegen x0 strebt. Als Formel geschrieben:
limx → x0
x ǂ x0
f(x) − f(x0)x − x0 = f’(x0).
Das ist die Formel, die oben bereits auf anschauliche Art vorgestellt wurde.
Ist c irgendeine konstante reelle Zahl, so ist unmittelbar klar, dass c’ = 0 und (c·x)’ = c.
![]() D8
D8
Sei M ⊂ ℝ zulässig und f eine auf M
definierte Funktion.
Wenn f in x0 ∈∈ M differenzierbar ist, dann ist f auch in x0
stetig.
Beweis:
Sei f in x0 ∈∈ M differenzierbar, dann existiert eine in x0 stetige
Funktion mit
f(x) = f(x0) + (x − x0)·Δ(x) für x ∈∈ M.
Die Aussage des Satzes ist bewiesen, wenn sowohl das Produkt als auch die Summe zweier stetiger Funktionen wieder stetig ist. Dies folgt aber unmittelbar aus dem Folgenkriterium zusammen mit den Grenzwertsätzen für Folgen.
Demzufolge kann eine in x0 nicht stetige Funktion dort auch nicht differenzierbar sein.
Aus der Differenzierbarkeit einer Funktion lässt sich auf die Stetigkeit der Funktion schließen (das wurde soeben bewiesen); die Umkehrung gilt dagegen nicht! Zum Beispiel ist die Betragsfunktion, die jeder rellen Zahl x ihren Absolutbetrag zuordnet, zwar in 0 stetig, aber dort nicht differenzierbar. Die auf einem Intervall [a, b] definierte Bolzanofunktion ist dort überall stetig, aber sogar nirgendwo differenzierbar.
Eine differenzierbare Funktion f kann oft (aber nicht immer!) mehrmals differenziert werden. Man schreibt dann
f(0) = f,
f(1) = f’,
f(2) = f’’,
...
f(n) = f(n-1)’ für n ≥ 1.
![]() D9 (Satz von Rolle)
D9 (Satz von Rolle)
Sei f eine auf [a, b] stetige und auf
(a, b) differenzierbare Funktion.
Wenn zudem f(a) = f(b) = c gilt, so gibt es
mindestens ein x0 ∈∈ (a, b)
mit f’(x0) = 0.
Beweis:
Es darf angenommen werden, dass f(x) = c
nicht für alle x ∈∈ [a, b]
gilt (andernfalls würde die Aussage des Satzes trivialerweise sofort folgen).
Nach dem Satz vom Minimum und Maximum nimmt
f auf dem Intervall [a, b] einen größten und einen kleinsten Wert an.
Fall 1: c ist nicht der
größte Funktionswert.
Dann gibt es ein x0 ∈∈ (a, b),
so dass für alle x ∈∈ [a, b] f(x0) ≥ f(x)
gilt. Wegen der Stetigkeit von f in
x0
kann man eine genügend kleine Umgebung U(x0)
so wählen, dass
für alle x ∈∈ U(x0) f(x0) − f(x) ≥ 0
gilt.
Da f in x0 nach Voraussetzung auch differenzierbar ist, existiert
sowohl der Grenzwert
mo = limx → x0
x > x0
f(x) − f(x0)x − x0
als auch der Grenzwert
mu = limx → x0
x < x0
f(x) − f(x0)x − x0
und es ist mo ≤ 0 bzw. mu ≥ 0. f’(x0) ist eindeutig bestimmt, also folgt
mo = mu = f’(x0) = 0.
Fall 2: c ist der größte Funktionswert.
Dann gibt es ein x0 ∈∈ (a, b),
so dass für alle x ∈∈ [a, b] f(x0) ≤ f(x)
gilt. Auf die gleiche Weise wie eben folgt f’(x0) = 0.
![]() D10 (Summen-,
Faktor- , Produkt- und Quotientenregel)
D10 (Summen-,
Faktor- , Produkt- und Quotientenregel)
Sei M ⊂ ℝ zulässig,
x0 ∈∈ M und k ∈∈ ℝ. f und g seien zwei auf M definierte und in
x0 differenzierbare Funktionen. Dann sind auch
f + g, k·f, f·g in x0
differenzierbar und es gilt:
(f + g)’(x0) = f’(x0)
+ g’(x0),
(k·f)’(x0) = k·f’(x0),
(f·g)’(x0) = f’(x0)·g(x0) + f(x0)·g’(x0).
Ist f(x0) ǂ 0, dann ist auch 1f in x0 differenzierbar und es gilt
(1f)’(x0) = − f’(x0)f(x0)2.
Ist g(x0) ǂ 0, dann ist auch fg in x0 differenzierbar und es gilt:
(fg)’(x0) = f’(x0)·g(x0)−f(x0)·g’(x0)g(x0)2
Beweis:
Es gibt eine in x0
stetige Funktion Δf mit
f(x) = f(x0) + (x − x0)·Δf(x) für alle
x ∈∈ M
und eine in x0
stetige Funktion Δg mit g(x) = g(x0) + (x − x0)·Δg(x) für alle
x ∈∈ M.
Damit hat man
(f + g)(x)
= f(x) + g(x)
= (f + g)(x0)
+ (x − x0)·(Δf + Δg)(x);
(Δf + Δg) ist auch stetig in x0,
also gilt die Summenregel.
Mit Δf ist auch k·Δf in x0 stetig und es gilt (k·f)(x) = (k·f)(x0) + (x − x0)·(k·Δf)(x) für alle x ∈∈ M, folglich gilt auch die zweite Ableitungsregel.
(f·g)(x)
= (f(x0) + (x − x0)·Δf(x))·(g(x0) + (x − x0)·Δg(x))
= (f·g)(x0) + (x−x0)·[f(x0)·Δg(x)
+ Δf(x)·g(x0) + (x − x0)·(Δf·Δg)(x)].
Die durch den Ausdruck in der eckigen Klammer definierte Funktion ist in x0 stetig und hat dort den Wert f(x0)·g’(x0) + f’(x0)·g(x0). Somit ist auch die Produktregel bewiesen.
Wenn f(x0) ǂ 0, dann gibt
es auf Grund der Stetigkeit von f in x0 ein ε > 0,
so dass f(x) ǂ 0 für alle
x ∈∈ M ∩
Uε(x0). Für diese x existiert 1f und es gilt
1f(x) − 1f(x0) = f(x0) − f(x)f(x)·f(x0).
Nach Voraussetzung ist f(x) − f(x0) = (x − x0)·Δf(x). Damit folgt
1f(x) = 1f(x0) + (x−x0)·Δf(x)f(x)·f(x0).
Die durch den Ausdruck Δf(x)f(x)·f(x0) definierte Funktion ist in x0 stetig und hat dort den Wert f’(x0)f(x0)2, was zu beweisen war.
Wegen fg = f · 1g folgt die Quotientenregel unmittelbar aus dem Vorhergehenden.
Seien M und N zulässige Mengen. f sei eine auf M und g eine auf N definierte Funktion. Wenn f(M) ⊂ N, dann lassen sich f und g miteinander verketten. Man definiert
(g◦f)(x) =def g(f(x)) für alle x ∈∈ M.
![]() D11
(Kettenregel)
D11
(Kettenregel)
Seien f: M → ℝ und g: N → ℝ miteinander verkettete Funktionen mit f(M) ⊂ N.
Wenn dann f in x0 ∈∈ M
und g in f(x0) ∈∈ N differenzierbar sind,
dann ist g◦f in x0 differenzierbar
und es gilt:
(g◦f)’(x0) = g’(f(x0))·f’(x0)
Beweis:
Es gibt eine in x0
stetige Funktion Δf mit
f(x) = f(x0) + (x − x0)·Δf(x) für alle x ∈∈ M
und eine in y0 = f(x0) stetige Funktion Δg mit
g(y) = g(y0) + (y − y0)·Δg(y) für alle y ∈∈ N.
Hieraus folgt
g(f(x))
= g(f(x0)) +
(f(x) − f(x0))·Δg(f(x))
= g(f(x0)) + (x − x0)·Δf(x)·Δg(f(x)).
Die auf M durch Δ(x) = Δf(x)·Δg(f(x)) definierte Funktion Δ ist stetig in x0. Es folgt die Behauptung.
![]() D12
D12
Sei f: ℝ → ℝ
eine Potenzfunktion, das heißt
f(x) = a·xn für x ∈∈ ℝ
mit a ∈∈ ℝ und n ∈∈ ℕ*. Dann gilt
f’(x) = a·n·x(n−1) für x ∈∈ ℝ.
Beweis (mit vollständiger Induktion):
Induktionsanfang:
f(x) = a·x1 = a·x ⇒
f’(x) = a ist offensichtlich richtig.
Induktionsvoraussetzung:
Angenommen, die Aussage (a·xm)’ = a·m·x(m−1)
für
x ∈∈ ℝ
sei bereits für ein m ∈∈ ℕ bewiesen.
Induktionsschluss:
(a·x(m+1))’
= (a·xm·x)’
= ((a·xm)·x)’
= a·m·x(m−1)·x + (a·xm)·1
= a·m·xm + a·xm
= a·(m+1)·xm
= a·(m+1)·x(m+1)−1, was zu beweisen war.
![]() D13 (Mittelwertsätze
der Differentialrechnung)
D13 (Mittelwertsätze
der Differentialrechnung)
(I)
Sei f eine auf [a, b] stetige und auf (a, b) differenzierbare Funktion.
Dann gibt es mindestens
ein x0 ∈∈ (a, b)
mit
f’(x0) = f(b) − f(a)b − a.
(II)
Seien f und g zwei auf [a, b] stetige und auf (a, b) differenzierbare Funktionen.
Für jedes x ∈∈ (a, b)
sei g’(x) ǂ 0. Dann
ist g(b) ǂ g(a) und es
gibt mindestens ein x0 ∈∈ (a, b)
mit
f(b) − f(a)g(b) − g(a) = f’(x0)g’(x0).
Beweis:
zu (I). Die durch
h(x) =def f(x) − f(b) − f(a)b − a·(x − a)
auf [a, b] definierte Funktion h ist wegen D3 dort überall stetig; außerdem ist h wegen D10 auf (a, b) differenzierbar und es gilt h(a) = h(b). Nach dem Satz von Rolle existiert somit ein x0 ∈∈ (a, b) mit
f’(x0) − f(b) − f(a)b − a = 0.
zu (II). Aus der Annahme g(a) = g(b)
folgt mit (I) die Existenz eines x0 ∈∈ (a, b)
mit g’(x0) = 0,
ein Widerspruch zur Voraussetzung. Demnach gilt g(b) ǂ g(a).
Die durch
H(x) =def f(x) − f(b) − f(a)g(b) − g(a)·(g(x) − g(a))
auf [a, b] definierte Funktion H erfüllt ebenso wie h die Voraussetzungen des Satzes von Rolle. Also gibt es ein x0 ∈∈ (a, b) mit
f’(x0) − f(b) − f(a)g(b) − g(a)·g’(x) = 0.
Hieraus folgt die behauptete Verhältnisgleichung.