Mathematische Begriffe
So wie Handwerker gepflegte Werkzeuge benötigen, um sinnvoll arbeiten zu können, brauchen Mathematiker sorgfältig definierte Begriffe, mit denen es möglich ist, mathematische Aussagen präzise zu formulieren und neue Gesetzmäßigkeiten herzuleiten.
Anhand ausgewählter Begriffe kann man auf diesen Seiten mathematische Arbeits- und Denkweisen studieren und grundlegende Beweisverfahren kennenlernen.
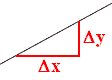 Änderungsrate
Änderungsrate
Sei f eine auf einem Intervall
[a, b] ⊂ ℝ erklärte und dort
stetige Funktion.
Sei ferner x0, x ∈∈ [a, b]
mit x ǂ x0. Dann heißt
f(x) − f(x0)x − x0
„Änderungsrate (oder Differenzenquotient) von f “. Dieser Quotient ist ein Maß für die Änderung der Funktionswerte von f zwischen x0 und x, und zwar relativ zu |x − x0|. Ist f in x0 nicht nur stetig, sondern auch differenzierbar, so strebt der Differenzenquotient für x → x0 gegen den Differentialqotienten
f’(x0) = limx → x0
x ǂ x0
f(x) − f(x0)x − x0.
Diese zentrale Formel der Differentialrechnung wird im Kapitel Änderungsrate zunächst anschaulich vorgestellt und danach mathematisch streng hergeleitet.
Stichworte: Steigungsfaktor, Durchschnittsgeschwindigkeit, Tangentenproblem, Differentialquotient, Rechnen mit Beträgen, Zahlenfolgen, Grenzwertsätze, Umgebung, Stetigkeit, Satz vom Minimum und Maximum, Zwischenwertsatz, Differenzierbarkeit, Satz von Rolle, Ableitungsregeln, Mittelwertsätze
 Äquivalenzrelation
Äquivalenzrelation
Auf der Grundlage der Menge der natürlichen Zahlen
ℕ = { 0, 1, 2, ... } lassen sich weitere
Zahlenmengen,
nämlich ℤ, ℚ, u.s.w. auf eine ganz eigentümliche Art
konstruieren. Der zentrale Begriff, mit dessen Hilfe diese Konstruktionen
möglich sind, ist der Begriff Äquivalenzrelation.
Auch in anderen Zusammenhängen ist dieser Begriff wichtig. Eine Menge M, auf der eine
Äquivalenzrelation ~ definiert
ist, zerfällt sozusagen von selbst in paarweise
disjunkte Teilmengen Mi, und zwar so,
dass für je zwei Elemente x und y einer Teilmenge Mi stets x ~ y
gilt. Das Umgekehrte ist ebenfalls richtig: Jede Zerlegung einer
Menge M induziert in natürlicher Weise eine Äquivalenzrelation auf M.
Beide Aussagen werden im Kapitel Äquivalenzrelation bewiesen.
Stichworte: Transitivität, Symmetrie, Reflexivität, Zerlegung, Quotientenmengen, Äquivalenzklassen, Repräsentant, Restklassen, Pfeilklassen
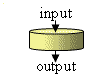 Algorithmus
Algorithmus
Ein Algorithmus besteht aus einer Folge von Anweisungen, nach denen man
unter Vorgabe von Eingangsdaten eine bestimmte Ausgabe erhält. Im Kapitel
Algorithmus findet man sowohl eine präzisere Beschreibung dieses
Begriffs als auch Beispiele solcher Anweisungsfolgen, angefangen beim Abakus
bis hin zur Schickard’schen Rechenmaschine, gefolgt von einem mit
JavaScript
programmierten Algorithmus zur Umrechnung von Zahlen. Der letzte Abschnitt
des Kapitels hat die Turingmaschine zum Gegenstand. Die von Alan Turing (1912−1954) entwickelte und nach ihm benannte
Turing machine ist ein mathematisches Modell eines Universalrechners.
Man geht davon aus, dass es grundsätzlich keine Rechenmaschine geben kann,
die rechenmächtiger ist als die Turingmaschine.
Stichworte: Abakus, Napier’sche Rechenstäbe, Gelosia-Methode, Schickard’sche Rechenmaschine, Darstellung von Zahlen, Stellenwertsystem, Imperatives Programmieren, Turingmaschine
 Ebene
Ebene
Euklid forderte mit den ersten beiden seiner fünf Postulate im I. Buch der Elemente, dass
„man von jedem Punkt nach jedem Punkt die Strecke ziehen“ und dass „man eine begrenzte gerade Linie
zusammenhängend gerade verlängern kann“. Auf Euklids Ebene, die man sich als ein flaches, unbegrenztes und nicht
gekrümmtes Gebilde vorstellen kann, lassen sich aufgrund gewisser Regeln geometrische Objekte zeichnen und
konstruieren. Dagegen haben die Axiome von David Hilbert (1862−1943), die
grundlegend für die Geometrie sind und im Kapitel Ebene der Reihe
nach vorgestellt werden, nicht von vornherein einen anschaulichen Bezug.
Jede geometrische Aussage darf nicht ad hoc (weil man es „so sieht“)
akzeptiert, sondern muss auf axiomatischer Basis bewiesen werden.
Stichworte: Ebene Inzidenzaxiome, Lineare Anordnungsaxiome, Axiom von Pasch, Satz von Moore, Lineare Kongruenzaxiome, Ebene Kongruenzaxiome, Nebenwinkel, Kongruenzsätze, Crossbar-Theorem, Basiswinkelsatz, Hilbertebene, Satz vom Außenwinkel, Parallelen, Streckenlängen, Winkelweiten, Strahlensätze, Kreise, Die kartesische Ebene
 Fläche
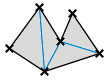
Fläche
Die Formel zur Bestimmung des Flächeninhalts eines Rechtecks mit der Breite
a und der Höhe b ist einfach: A = a·b.
Nicht ganz so einfach ist es, zu beweisen, dass diese Formel für alle
Rechtecke gültig ist. Um die Flächeninhalte von irgendwelchen (einfachen) Polygonen
bestimmen zu können, wird eine Abbildung benötigt, die jedem Polygon bzw. dessen Fläche eine positive reelle Zahl
eindeutig zuordnet. Im Kapitel Fläche geht
es unter anderem um diese Abbildung (dem so genannten Flächenmaß) und
deren Eigenschaften. Ein Flächenmaß setzt voraus, dass
man Streckenlängen messen kann. Es ist allerdings sinnvoll, auch ohne
die Messbarkeit von Längen von dem Inhalt von Flächen zu sprechen. Die
zentralen Begriffe sind dann Zerlegungsgleichheit
und Inhaltsgleichheit von Polygonflächen.
Stichworte: Rechteckflächen, Flächen- und Längeneinheiten, Der Meter, Einfache Polygone, Zwei-Ohren-Theorem, Polygonflächen, Flächenmaß, Fläche eines Dreiecks, Fläche eines Parallelogramms, Isometrien, Zerlegungsgleichheit und Inhaltsgleichheit, Satz von Bolyai-Gerwien, Satz des Pythagoras
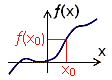 Funktion
Funktion
Leonhard Euler (1707−1783) verstand unter einer
Funktion einer veränderlichen Größe einen analytischen Ausdruck, der
irgendwie aus der veränderlichen Göße und aus Zahlen oder konstanten Größen
zusammengesetzt ist. Wenn man dieses in die heutige mathematische Sprache
übersetzt, denkt man am ehesten an Funktionsterme wie beispielsweise 2·π·r
für den Umfang eines Kreises in Abhängigkeit vom Kreisradius r. Johann Peter Gustav Lejeune Dirichlet (1805−1859) gab die
Vorstellung von zwei unbedingt gesetzmäßig miteinander verknüpften
Größen ganz auf und sprach von einer Funktion bereits
dann, wenn zu jedem Wert einer veränderlichen Größe x innerhalb eines
bestimmten Intervalls genau ein endlicher Wert von y gehört. An der Dirichlet’schen Auffassung des Funktionsbegriffs hat sich von der
Idee her nichts geändert. Dem entsprechend werden die Begriffe „Abbildung“
und „Funktion“ im Kapitel Funktion in heute üblicher Weise definiert.
Stichworte: Schaubild, Proportionalität, Funktionsgleichung, Quadratische Funktion, Exponentielle Funktion, Parameter, Polarkoordinaten, Abbildung, Plimpton 322, Umkehrfunktionen
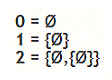 Menge
Menge
Wenn gewisse Objekte x eine gemeinsame Eigenschaft E haben,
liegt es nahe, all diese einzelnen Objekte zu einer „Menge“
zusammenzufassen. In formaler Schreibweise:
ME =def { x | E trifft zu auf x }.
Diesen Vorgang der Mengenbildung nennt man Komprehension. Das sogenannte Komprehensionsprinzip, welches besagt, dass man diese Art der Mengenbildung immer vornehmen kann, führt in der „naiven“ Mengenlehre zu logischen Widersprüchen. Ernst Zermelo (1871−1953) hat eine axiomatisch begründete Theorie entwickelt mit dem Ziel, diese Widersprüche auszuschließen. Spätere Ergänzungen von Zermelos Prinzipien führten schließlich zum Zermelo-Fraenkel’schen Axiomensystem mit Auswahlaxiom (Axiom of Choice), in der mathematischen Literatur abgekürzt mit ZFC. Das Kapitel Menge ist eine Einführung in die Grundlagen der Mengenlehre auf der Basis von ZFC.
Stichworte: Nicht-axiomatische Mengenlehre, Verknüpfungstafeln, Antinomien, Zermelo-Fraenkel’sche Axiome, Relationen und Funktionen, vonNeumann’sche Zahlen, Rekursionssatz für ω, Endliche Mengen, Fundierte Strukturen, Ordinalzahlen, Satz von Hartogs, Wohlordnungssatz, vonNeumann’sche Hierarchie, Mächtigkeiten, Kardinalzahlen
 Reihe
Reihe
Im vom indischen Mathematiker und Astronom Nīlakaṇṭha Somayājī um 1500 geschriebenen Werk Tantrasaṅgraha
findet sich eine von Mādhava etwa 100 Jahre zuvor entdeckte Anleitung zur Berechnung der
Kreiszahl π, in heutiger Schreibweise:
π4 = 1 − 13
+ 15
− 17
+ 19
− 111 + −...
Es ist eine der verblüffendsten und schönsten Formeln der Mathematik: π
ist nach dieser Formel darstellbar mit einer alternierenden und nicht
abbrechenden Summe aller Bruchzahlen mit ungeraden Nennern. Der Beweis der
Formel von Mādhava setzt Kenntnisse voraus, die im Kapitel Reihe vermittelt werden.
Stichworte: Mādhava-Leibniz-Reihe, Summenfolge, Geometrische Reihe, Euler'sche Reihe, Exponentialreihe, Konvergenzkriterien, Gleichmäßige Konvergenz, Potenzreihen, Taylorpolynome und Taylorreihen, Nicht-algebraische elementare Funktionen
 Rückkopplung
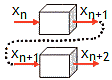
Rückkopplung
Man nimmt eine Figur, steckt sie in eine
Verkleinerungsmaschine und erhält eine um den Faktor k
verkleinerte Figur; man nimmt die um den Faktor k verkleinerte Figur,
steckt sie in dieselbe Verkleinerungsmaschine und erhält so durch eine
einfache Rückkopplung ein recht einfaches und eher langweiliges Resultat:

eine Folge von gleichmäßig kleiner werdenden selbstähnlichen Figuren. Hieraus kann jedoch nicht der Schluß gezogen werden, dass ein einfacher Rückkopplungsprozess („was hinten rauskommt, wird vorn wieder reingesteckt“) immer einfache Ergebnisse liefert. Das Kapitel Rückkopplung bietet einen kurzen Einblick in einige interessante Rückkopplungsprozesse.
Stichworte: Chaos im Reellen, Chaos im Komplexen, Mandelbrotfolgen
 Vektor
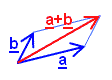
Vektor
Die physikalischen Größen Geschwindigkeit, Kraft, Beschleunigung, Impuls und viele andere
gehören zu den „gerichteten Größen“, die durch Betrag und Richtung
charakterisiert sind. Gerichtete Größen können als Vektoren aufgefasst
werden, die in anschaulicher Weise durch Pfeile repräsentiert werden. Im
allgemeinen Sinne sind Vektoren Elemente eines Vektorraumes über einem
Körper K. Ist (V,+) eine Abel’sche
Gruppe mit
einer additiven Verknüpfung „+“: VxV → V,
so versteht man unter einem K-Vektorraum eine
algebraische Struktur (V,K,·)
mit einer äußeren multiplikativen Verknüpfung
„·“: KxV → V, für
die bestimmte Rechenregeln gelten. Das Kapitel Vektor
vermittelt einige grundlegende Kenntnisse über das Rechnen mit Vektoren und deren Anwendung.
Stichworte: Skalare Größen, Gerichtete Größen, Pfeilklassen, K-Vektorräume, Ortsvektoren, Skalarprodukt, Normalenvektor, Euklidische Vektorräume, Kreuzprodukt, Skalare Felder, Vektorfelder
 Verhältnis
Verhältnis
Bildet man den Quotienten aus zwei Zahlenwerten oder aus zwei Größen, um vergleichbare Dinge zueinander in Beziehung
zu setzen, so nennt man diesen Quotienten „Verhältnis“. Viele physikalische Größen sind definiert als
Verhältnis zweier verschiedener Größen, so zum Beispiel die Dichte
ρ als Verhältnis der Masse eines homogenen Körpers zu seinem Volumen. Setzt
man zwei Verhältnisse einander gleich, so erhält man eine
Verhältnisgleichung. Solche, etwa für die Prozentrechnung, innerhalb der
Geometrie oder in der Physik wichtigen Verhältnisgleichungen
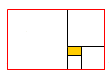
sind Gegenstand des Kapitels Verhältnis. Das vielleicht schönste Verhältnis
wird von der den goldenen Schnitt charakterisierenden Verhältnisgleichung geliefert.
Stichworte: Säulendiagramme, Prozentrechnung, Brechungsgesetz von Snellius, Harmonische Punkte, Musikalische Intervalle, Proportionen, Der goldene Schnitt, Pentagramm, Lucas-Folgen, Kettenbrüche
 Vollständige Induktion
Vollständige Induktion
Der wesentliche Inhalt des Kapitels Vollständige Induktion
besteht im Beweis aller Rechenregeln, die in der Menge der natürlichen
Zahlen (ℕ) gelten, sowie dem Beweis,
dass ℕ
wohlgeordnet ist. Allen diesen Beweisen
liegt das Prinzip der vollständigen Induktion zugrunde. Sei mit „E(n)“ irgendeine Aussage bezeichnet, die in
Abhängigkeit von n ∈∈ ℕ
formuliert werden kann. Wenn „ℰ(n)“
die Abkürzung für „Die Aussage E(n) ist wahr“ bedeutet, dann lautet das Induktionsprinzip wie folgt:
Gilt für m ∈∈ ℕ
(i) ℰ(0) und
(ii) ℰ(m) ⇒ ℰ(succ(m)),
so folgt: ℰ(n) für alle n ∈∈ ℕ.
Stichworte: Peano’sche Axiome, Prinzip der vollständigen Induktion, Kette, Geordnete Mengen, 2-stellige Operation, Addieren und Multiplizieren natürlicher Zahlen, Dezimalzahlen, Binomischer Lehrsatz, Ungleichung von Bernoulli, Turm von Hanoi
 Wahrscheinlichkeit
Wahrscheinlichkeit
Wahrscheinlichkeitsaussagen beziehen sich zwar immer auf einzelne
zukünftige Ereignisse als mögliche Resultate eines Zufallsexperimentes,
sind aber nur dann sinnvoll, wenn sie auf Beobachtungen beruhen, die während
einer sehr großen Zahl von Durchläufen des gleichen Zufallsexperimentes zuvor gemacht worden sind.
Das Kapitel Wahrscheinlichkeit beinhaltet die Regeln, nach
denen Wahrscheinlichkeitswerte berechnet werden können. Die Grundformel zur Berechnung von Wahrscheinlichkeiten im Zusammenhang von
Laplace-Experimenten ist besonders einfach. Für jedes
Ereignis E eines solchen Experimentes gilt
P(E) = |E||S|.
Hierbei ist |E| die Anzahl der Elemente in der Ereignismenge E und |S| die Anzahl der Elemente in der Ergebnismenge S.
Stichworte: Ereignis, Häufigkeit, Zufallsexperiment, Venn-Diagramme, Kolmogorow'sche Axiome, Additionssätze, Multiplikationssatz, Kombinatorik, Binomialkoeffizient, Lotto, Zufallsvariablen, Baumdiagramm, Nadelproblem von Buffon
 Zahlen
Zahlen
Wir können Zahlen in verschiedensten Zusammenhängen nutzen, wir können sie
auf unterschiedliche Weise darstellen und wir können unter Beachtung von
Rechenregeln Eigenschaften von Zahlen auf logische Art schlussfolgern, ohne
zu wissen, was Zahlen „eigentlich“ sind. Wenn man bei einer Zahl von ihrer
Bedeutung, von ihren Eigenschaften und von ihrer Darstellung absieht, was
bleibt dann? Alle, die sich um den Begriff der Zahl Gedanken gemacht haben, starten zunächst mit der Frage: Was ist
eine natürliche Zahl? Oder in alter Sprechweise: Was ist eine „ganze“ Zahl?
Richard Dedekind (1831−1916)
war der Erste, dem es gelang, die Gesamtheit der natürlichen Zahlen
durch die Aufstellung von vier Bedingungen vollständig zu charakterisieren.
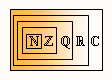
Im Kapitel Zahlen wird gezeigt, wie Schritt für Schritt und
aufeinander aufbauend die Zahlenmengen ℕ,
ℤ, ℚ,
ℝ und ℂ
definiert werden können. Im Kapitel Menge
kann man darüber hinaus lernen, dass und wie der Begriff der Zahl mittels der
vonNeumann’schen Zahlen auf den Mengenbegriff zurückgeführt werden kann.
Stichworte: Natürliche Zahlen, Ganze Zahlen, Irrationale Zahlen, Algebraische Struktur, Rationale Zahlen, Trichotomie, Absolutbetrag, Reelle Zahlen, Cauchyfolge, Metrischer Raum, Archimedisch angeordnete Körper, Vollständigkeit, Satz von Bolzano-Weierstraß, Intervallschachtelung, Transzendente Zahlen, Komplexe Zahlen
Fast alle Kapitel beginnen mit einer anschaulich gehaltenen Einführung in das jeweilige Thema. Der Schwierigkeitsgrad der einzelnen Seiten ist sehr unterschiedlich: das Kapitel Wahrscheinlichkeit ist vielleicht das anschaulichste von allen; die Kapitel Zahlen und Menge sind sicherlich am anspruchsvollsten.
Die Herleitungen und Beweise sind kleinschrittig ausformuliert, so dass
auch AnfängerInnen der Mathematik - Geduld und Hartnäckigkeit vorausgesetzt -
alles gut nachvollziehen und verstehen können. Wo es sich anbietet, finden
sich historische Bezüge und es gibt an den entsprechenden Stellen Verweise auf
mathematische Originalliteratur.
Wenn die folgende Liste lesbar
dargestellt wird, dann werden auch alle anderen Seiten korrekt angezeigt.
| ℕ | Menge der natürlichen Zahlen |
| ℤ | Menge der ganzen Zahlen |
| ℚ | Menge der rationalen Zahlen |
| ℝ | Menge der reellen Zahlen |
| ℂ | Menge der komplexen Zahlen |
| ∈∈ | ist Element von Beispiel: 0 ∈∈ ℕ |
| ∉∉ | ist kein Element von Beispiel: 12 ∉∉ ℤ |
| ⊂ | ist eine echte Teilmenge von Beispiel: {0,1,2} ⊂ ℕ |
| ∪ | vereinigt mit Beispiel: {0,1} ∪ {1,2} = {0,1,2} |
| ∩ | geschnitten mit Beispiel: {a,b,c} ∩ {b,d} = {b} |
| \ | ohne Beispiel: ℕ \ {0} = ℕ* |
| =def | wird definiert als Beispiel: 1 =def succ(0) |
| = | gleich Beispiel: 3! = 1·2·3 = 6 |
| ǂ | ungleich Beispiel: 13 ǂ 0,3 |
| ≈ | ungefähr gleich Beispiel: π ≈ 355113 |
| < | kleiner als Beispiel: 15 < 14 |
| > | größer als Beispiel: 0 > −1 |
| ≤ | kleiner als oder gleich Beispiel: (−∞, 0] = {x ∈∈ ℝ: x ≤ 0} |
| ≥ | größer als oder gleich Beispiel: [0, ∞) = {x ∈∈ ℝ: x ≥ 0} |
| | | ist Teiler von Beispiel: 2 | 6 |
∤ |
ist kein Teiler von Beispiel: 2 ∤ 7 |
∧ |
und |
∨ |
oder |
| ⇒ | daraus folgt Beispiel: x < −2 ⇒ x2 > 4 |
| ⇔ | ist äquivalent zu Beispiel: |x| = 1 ⇔ (x = 1 ∨ x = −1) |
| → | strebt gegen Beispiel: 1n → 0 (n → ∞) |
| ↦ | wird abgebildet auf Beispiel: x ↦ f(x) |
