Maple-Worksheet: Lissajous

Einführung in Maple Anwendungen

Physik

Lissajousfiguren

>	restart; with (plots): Warning, the name changecoords has been redefined

Fall 1: Zwei zueinander senkrecht stehende Schwingungen mit
Phasendifferenz Ф und gleichgroßer Kreisfrequenz ω:

>	glx:= x = x[0]cos(omegat): glx; gly:= y = y[0]cos(omegat + phi): gly;

Eliminieren von t liefert:

>	eliminate ({glx, gly}, {t});

Es ergibt sich eine Gleichung in x und y :

>	gl:= op (1,op (2, %))= 0: gl;

Umformen dieser Gleichung:

>	gl:= expand (gl/(x[0]^2*y[0]^2)): gl; gl:= sort(gl): gl;

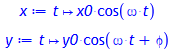
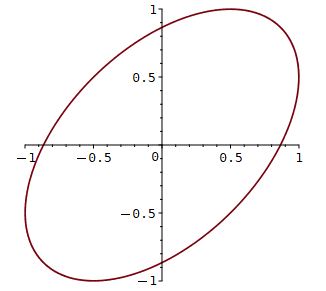
Zahlenbeispiel mit Schaubild:

>	x[0]:= 1: y[0]:= 1: phi:= Pi/3: gl; implicitplot (gl, x = -2..2, y = -2..2, color = red);

Lissajousfigur

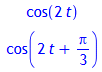
Fall 2: Zwei zueinander senkrecht stehende Schwingungen mit
Phasendifferenz Ф und unterschiedlichen Kreisfrequenzen:

>	restart; with (plots): x:= t -> x0cos(omegat); y:= t -> y0sin(komega*t + phi);

Warning, the name changecoords has been redefined

Zahlenbeispiel mit Schaubild:

>	x0:= 1: y0:= 1: omega:= 2: k:= 2/3: phi:= Pi/4: x(t); y(t); plot ([x(t), y(t), t = 0..4*Pi]);

Lissajousfigur

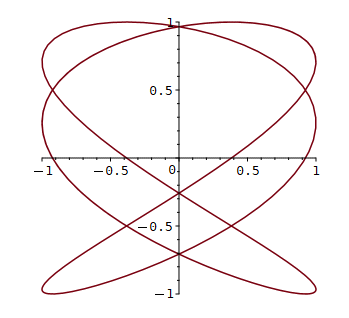
"Oszilloskopbild" bei variierender Phasenverschiebung Ф:

>	phi:= 'phi': animate ([x(t), y(t), t = 0..4Pi], phi = 0..2Pi, frames = 80, numpoints = 1000, axes = NONE, color = magenta);