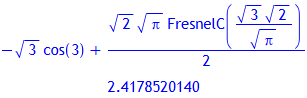Das Simpsonverfahren
> restart;
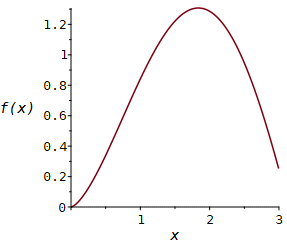
Definition einer Funktion:
> f:= x -> sqrt(x)*sin(x);
plot(f(x), x = 0..3,
font = [Courier, 10],
labelfont = [Courier, 12],
labels = [x, "f(x)"],
size =[300, 250]);
font = [Courier, 10],
labelfont = [Courier, 12],
labels = [x, "f(x)"],
size =[300, 250]);
![]()
Das Integral A soll numerisch, und zwar mit Hilfe der Simpsonformel, berechnet werden:
> A:= Int (f(x), x = 0..3);
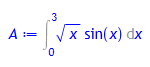
> Simpson:= proc(a, b, n)
local i, j, h, fx, s:
h:= (b-a)/n;
for i from 0 to n do
fx[i]:= evalf(f(a + i*h));
od:
s:= fx[0] + fx[n]:
s:= s + 2*sum(fx[2*j], j = 1..(n/2-1)):
s:= s + 4*sum(fx[2*j+1], j = 0..(n/2-1)):
1/3*s*h:
end:
Simpson(0, 3, 10);
Simpson(0, 3, 100);
Simpson(0, 3, 1000);
h:= (b-a)/n;
for i from 0 to n do
fx[i]:= evalf(f(a + i*h));
od:
s:= fx[0] + fx[n]:
s:= s + 2*sum(fx[2*j], j = 1..(n/2-1)):
s:= s + 4*sum(fx[2*j+1], j = 0..(n/2-1)):
1/3*s*h:
end:
Simpson(0, 3, 10);
Simpson(0, 3, 100);
Simpson(0, 3, 1000);
![]()
![]()
![]()
Die Lösung des gegebenen Integrals durch Maple:
> value(A);
evalf(%);