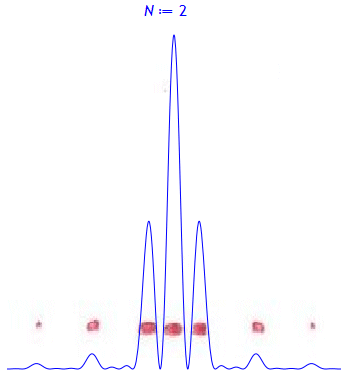
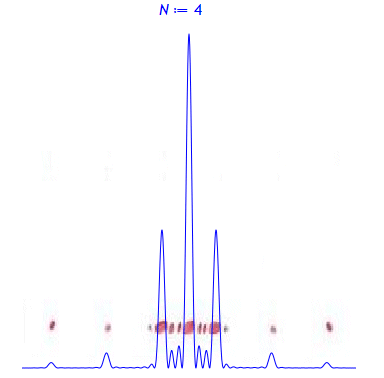
Lichtbeugung am Mehrfachspalt
> restart; with(plots):
interface(displayprecision = 3):
N = Anzahl der Spalte im Mehrfachspalt:
b = Spaltbreite in m:
g = Abstand benachbarter Spalte in m :
λ = Wellenlänge des benutzten Lichtes in m:
Gangunterschied benachbarter Wellenzüge bei einem optischen Gitter:
> Delta[Gitter]:= g*sin(phi);
![Delta[Gitter] := g*sin(phi)](images-beugung/beugung2.gif){kind=small}
Die zugehörige Phasendifferenz:
> delta[Gitter]:= 2*Pi*Delta[Gitter]/lambda;
Normierte Intensitätsverteilung hinter dem Gitter:
> J[Gitter]:= (sin(N*delta[Gitter]/2)/(sin(delta[Gitter]/2)))^2;
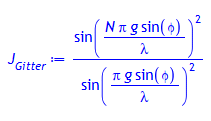
Normierte Intensitätsverteilung hinter einem Spalt:
> J[Spalt]:= sin(Pi*b*sin(phi)/lambda)^2/(Pi*b/N*sin(phi)/lambda)^2;
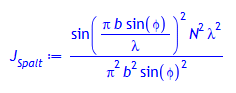
Normierte Intensitätsverteilung hinter einem Mehrfachspalt:
> J[Mehrfachspalt]:= J[Spalt]*J[Gitter];
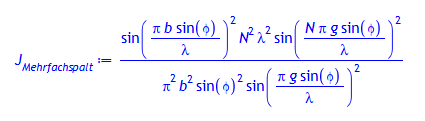
Intensitätsverteilung von Beugungsbildern auf einem 3m entfernt stehenden ebenen Schirm:
J:= unapply(%, [N, b, g, lambda]);
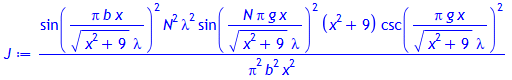
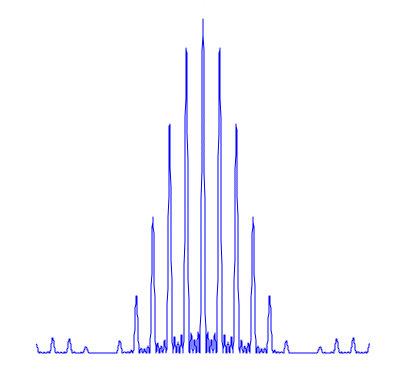
Zeichnen eines Beugungsbildes:
(The
adaptive option was updated in Maple 2022.)
opts:= 'x = -xMax..xMax,
color = blue,
thickness = 0,
size = [350, 350],
adaptive = true,
axes = none':
plot (J(5, 0.05E-3, 0.3E-3, 500E-9), opts);
Reale Experimente mit rotem Laserlicht (λ = 632,8nm, b =
0,05mm, g = 0,1mm):
g:= 0.1E-3;
lambda:= 632.8E-9;
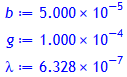
Einbinden zweier Beugungsbilder (..\Maple 2024\data\images\*.jpg):
img2 := FileTools:-JoinPath([ddir, "images","laser4.jpg"]):
Die Beugungsbilder im Vergleich mit den berechneten Intensitätsverteilungen:
