Verhältnis
ausführlich behandelt im Kapitel Mathematische Begriffe/Verhältnis
Bildet man den Quotienten aus zwei Zahlenwerten oder aus zwei Größen, um vergleichbare Dinge zueinander in Beziehung zu setzen, so nennt man diesen Quotienten Verhältnis.
Setzt man zwei Verhältnisse einander gleich, so erhält man eine Verhältnisgleichung.
Viele physikalische Größen sind definiert als Verhältnis zweier verschiedener Größen, so zum Beispiel die Dichte ρ als Verhältnis der Masse eines homogenen Körpers zu seinem Volumen, oder die Geschwindigkeit v eines sich gleichförmig bewegenden Körpers als Verhältnis zwischen dem zurück gelegten Weg und der dafür benötigten Zeit, oder die Kapazität eines Kondensators als Verhältnis der Kondensatorladung zur angelegten elektrischen Spannung.
Verhältnisgleichungen sind grundlegend wichtig, etwa für die Prozentrechnung, innerhalb der Geometrie (Beispiel: Strahlensätze) oder in der Physik (Beispiel: Snellius’sches Brechungsgesetz).
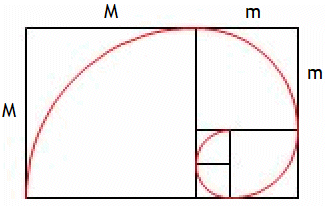
Das vielleicht schönste Verhältnis liefert die den goldenen Schnitt charakterisierende Verhältnisgleichung
Mm = M+mM.
Das Verhältnis Mm wird üblicherweise mit Φ (Phi) bezeichnet und goldene Zahl genannt. Es gilt
Φ = 1 + 1Φ = 1+√52 ≈ 1,618.
Ist die Länge eines Rechtecks exakt Φ-mal so groß wie seine Breite, so nennt man es ein goldenes Rechteck. Bei der Konstruktion der Fibonaccipirale entsteht auf natürliche Weise gleichzeitig eine Folge von goldenen Rechtecken:
→ Index
