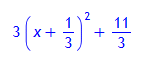Termumformungen
> restart;
assume(a, positive):
interface(showassumed = 0):
interface(showassumed = 0):
Zusammenfassen von Termen:
> combine((x^b)^2);
combine(2^x*2^y);
combine(sqrt(3*a)*sqrt(7*a^3));
combine(exp(b+ln(c))*exp(d));
combine(sqrt(3*a)*sqrt(7*a^3));
combine(exp(b+ln(c))*exp(d));
![]()
![]()
![]()
![]()
Vereinfachen von Termen:
> simplify(4^(1/2)*3*b);
simplify(sqrt(a*c)*sqrt(a*b), power);
![]()
![]()
> 5*sqrt(a)*sqrt(b) - 2*sqrt(a*b);
simplify(%, symbolic);
simplify(sqrt(x^2)) assuming (x > 0);
simplify(sqrt(x^2)) assuming (x < 0);
simplify(sqrt(x^2)) assuming (x > 0);
simplify(sqrt(x^2)) assuming (x < 0);
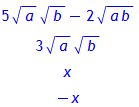
Ausmultiplizieren:
> expand((5+x)^2*(x^2 - 8));
![]()
Ausklammern:
> factor(3*x*y^2 - 9*y*x^3);
collect(b*sqrt(x)-sqrt(x)*b^2, sqrt(x));
![]()
![]()
Faktorisieren von Polynomen:
> factor(x^9 - x^3);
factor(x^2 - 1);
factor(x^2 - 2); # !
factor(x^2 - 2.0);
factor(x^2 - b^2);
factor(x^2 - 2); # !
factor(x^2 - 2.0);
factor(x^2 - b^2);
![]()
![]()
![]()
![]()
![]()
Faktorisieren von ( x2 − c):
> factor(x^2 - c);
lgn:= solve(x^2 - c, x);
factor(x^2 - c, lgn[1]);
factor(x^2 - c, lgn[1]);
![]()
![]()
![]()
Prüfen zweier Terme auf Äquivalenz:
> verify(x^2-y^2, (x+y)*(x-y), equal);
verify(sqrt(x+y), sqrt(x)+sqrt(y), equal);
![]()
![]()
Umformen des Terms q:
> q:= 3*x^2 + 2*x + 4;
Student[Precalculus][CompleteSquare](q);
![]()
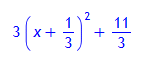
Abkürzen bzw. Umbenennen von Prozeduraufrufen:
> macro(quadrErg = Student[Precalculus][CompleteSquare]):
quadrErg(q);