Packages
(ausgewählte Prozeduren)
combinat
Kombinatorische Funktionen
with(combinat):
berechnet den Binomialkoeffizienten (n über k).
35
berechnet alle Kombinationen von k Elementen aus einer n-elementigen Menge.
choose(3, 2);
[[1, 2], [1, 3], [2, 3]
berechnet alle Listen mit k Zahlen, deren Summe jeweils n ergeben.
{ [2, 1, 1], [1, 2, 1], [1, 1, 2] }
berechnet die Anzahl aller k-elementigen Kombinationen aus einer n-elementigen Menge.
45
berechnet die Anzahl aller Partitionen einer integer-Zahl n.
5
berechnet die Anzahl aller k-elementigen Permutationen aus einer n-elementigen Menge.
90
berechnet alle Partitionen einer integer-Zahl z.
berechnet alle k-elementigen Permutationen aus einer n-elementigen Menge.
permute([a, b, c], 2);
berechnet eine Zufallsfolge von k Zahlen zwischen 0 und n.
berechnet eine zufällig gewählte Partition einer integer-Zahl z.
![]() Eigenschaften einer Binomialverteilung
Eigenschaften einer Binomialverteilung
geometry
![]()
2-dimensionale euklidische Geometrie
with(geometry):
definiert einen Kreis K durch drei Punkte P, Q und R.
point(Q, [2,3]):
point(R, [3,5]):
circle(K, [P,Q,R]);
K
definiert einen Kreis K durch seinen Mittelpunkt M und seinen Radius r.
circle(K, [M,2.3], [x,y]);
K
definiert eine Gerade g durch zwei Punkte P und Q.
g
definiert eine Gerade g durch eine Gleichung.
g
point (P, x, y);
definiert einen Punkt P durch seine ebenen Koordinaten.
P
definiert ein Quadrat Q durch vier Punkte.
point(S, [0,1]):
point(T, [1,1]):
point(U, [1,0]):
square(Q, [R,S,T,U]);
Q
definiert ein Dreieck T durch drei Punkte.
T
definiert ein Dreieck T durch drei Seitenlängen.
T
liefert die Koordinatenwerte eines Punktes M.
[-2, 0]
informiert über das geometrische Objekt Obj.

liefert die Koordinatengleichung eines Objekts.
berechnet die Fläche einer ebenen Figur.
ermittelt den Mittelpunkt eines Kreises.
M
ermittelt den Schwerpunkt C eines Vielecks.
point(Q,1,3):
point(R,-2,7):
point(S,-4,2):
centroid(C, [P,Q,R,S]):
coordinates(C);
berechnet den Abstand zweier geometrischer Objekte Obj1 und Obj2.
point(M, [-2,0]):
distance(P, M);
line(g, y = 3*x + 1, [x,y]):
distance(P, g);
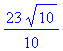
berechnet den Winkel zwischen Obj1 und Obj2 im Bogenmaß.
evalf(FindAngle(g, h), 4);
1.571
berechnet den Schnitt von zwei Objekten.
detail(S);
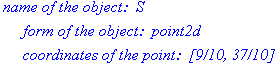
berechnet den Mittelpunkt M der Strecke AB.
point(B,1,3):
midpoint(M, A, B):
coordinates(M);
berechnet den Radius eines Kreises.
radius(K);
2.3
berechnet die Steigung einer Geraden.
slope(g);
3
liefert den Inkreis k eines Dreiecks T.
incircle(Inkreis, T):
radius(Inkreis);
liefert den Umkreis k eines Dreiecks T.
coordinates(center(Umkreis));
prüft, ob zwei Objekte Obj1 und Obj2 parallel zueinander sind oder nicht.
line(h, y = -1/3*x + 4, [x,y]):
AreParallel(g, h);
false
prüft, ob zwei Objekte O1 und O2 senkrecht aufeinander stehen oder nicht.
true
prüft, ob zwei Objekte Obj1 und Obj2 ähnlich zueinander sind oder nicht.
triangle(T2, [16,30,34]):
AreSimilar(T1, T2);
true
prüft, ob ein Punkt P oder eine Liste von Punkten auf einer Geraden g liegt.
IsOnLine(P, g);
false
prüft, ob ein Punkt A oder eine Liste von Punkten auf einem Kreis K liegt.
false
prüft, ob ein Dreieck T rechtwinklig ist.
true
![]() Das
Sierpinski-Dreieck
Das
Sierpinski-Dreieck
![]() Die
Eulergerade
Die
Eulergerade
geom3d
![]()
3-dimensionale euklidische Geometrie
with(geom3d):
definiert eine Gerade g durch zwei Punkte P und Q.
g
definiert eine Gerade g durch einen Punkt und einen Richtungsvektor.
g
definiert einen Punkt P durch seine Koordinaten.
P
definiert eine Ebene E durch eine Koordinatengleichung.
E
definiert eine Ebene E durch drei Punkte.
point(B, [5,-7,3]):
point(C, [1,6,4]) :
plane(E, [A,B,C]);
E
definiert eine Kugel K durch ihren Mittelpunkt M und ihren Radius r.
sphere(K, [M,2.3]);
K
definiert ein Dreieck T durch drei Punkte.
T
liefert die Koordinatenwerte eines Punktes P.
[-1,3,2]
informiert über das geometrische Objekt Obj.

liefert die Koordinatengleichung eines Objekts.
berechnet die Fläche eines Dreiecks oder einer Kugel.

berechnet den Mittelpunkt einer Kugel.
[-2,7,5]
berechnet den Abstand zweier geometrischer Objekte Obj1 und Obj2.
line(g, [point(P, [1,3,1]), [5,2,2]]):
evalf(distance(g, A));
1.749458790
berechnet den Winkel zwischen Obj1 und Obj2 im Bogenmaß.
plane(E, 2*x+3*y+z = 1, [x,y,z]);
evalf(FindAngle(g, E), 5);
0.99256
berechnet den Schnitt von zwei oder drei Objekten.
detail(S);
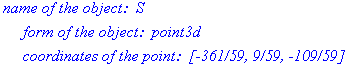
berechnet den Mittelpunkt M der Strecke AB.
point(B, [5,-7,3]):
midpoint(M, A, B):
coordinates(M);
berechnet den Radius einer Kugel.
2.3
berechnet das Volumen einer Kugel (und auch anderer Körper).
testet auf Kollinearität dreier Punkte.
point(B, [5,-7,3]):
point(C, [1,6,4]) :
AreCollinear(A, B, C);
false
testet auf Koplanarität von vier Punkten.
AreCoplanar(A, B, C, M);
false
prüft, ob zwei Objekte Obj1 und Obj2 parallel zueinander sind oder nicht.
false
prüft, ob zwei Objekte Obj1 und Obj2 senkrecht aufeinander stehen oder nicht.
ArePerpendicular(E, n);
true
prüft, ob ein Punkt A oder eine Liste von Punkten auf Obj liegt.
true
![]() Punkte im Raum
Punkte im Raum
![]() Relative
Lage von Geraden
Relative
Lage von Geraden
![]() Punkte,
Geraden und Ebenen
Punkte,
Geraden und Ebenen
![]() Der Schnitt
von Ebenen
Der Schnitt
von Ebenen
![]() Kugeln,
Ebenen und Geraden
Kugeln,
Ebenen und Geraden
LinearAlgebra
![]()
Lineare Algebra
with(LinearAlgebra):
definiert einen dreidimensionalen Zeilenvektor.
w:= <3| -2| 1/2>;
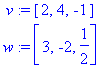
definiert einen dreidimensionalen Spaltenvektor.
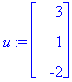
definiert eine mxn - Matrix.
M:= Matrix(3, 3, koeff);
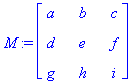
definiert eine mxn - Matrix.
M:= Matrix(3, 3, koeff);
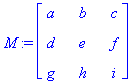
berechnet das Kreuzprodukt von v und w.
[0, -4, -16]
löscht Spalten der Matrix M.
löscht Zeilen der Matrix M.
berechnet die Determinante der Matrix M.
berechnet das Skalarprodukt von v und w.
addiert zwei Matrizen.
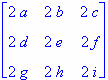
berechnet die inverse Matrix von M.
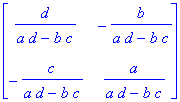
multipliziert zwei Matrizen miteinander.
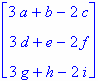
transponiert die Matrix M.

addiert zwei Vektoren mit gleicher Orientierung.
berechnet den Winkel zwischen v und w im Bogenmaß.
1.7
berechnet die 2-Norm (den "Betrag") eines Vektors.
VectorNorm(v, 2);
![]() Rechnen mit Vektoren
Rechnen mit Vektoren
![]() Rechnen mit Matrizen
Rechnen mit Matrizen
plots
![]()
Grafik
with(plots):
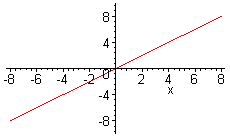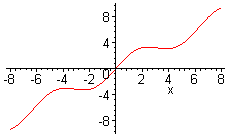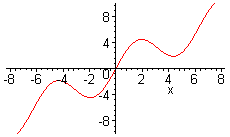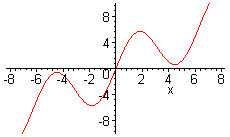
definiert eine Animationsfolge von Schaubildern einer Funktionenschar.
Hierbei ist t der Scharparameter; der frames-Wert gibt die Anzahl der zu zeichnenden Schaubilder an.
animate(f(t,x),
x = -8..8,
t = 0..4,
view = -10..10,
frames = 50);
arrow (v, Optionen);
definieren jeweils einen Vektor in einem dreidimensionalen Koordinatensystem.
color = red,
thickness = 2,
orientation = [-39, 63],
axes = normal);
view = [-5..5, -5..5],
grid = [3, 3],
color = grey,
linestyle = [SOLID, SOLID]):
display(KoordSys);
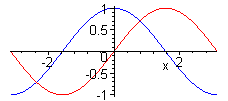
zeichnet Plot1, Plot2, usw. in ein gemeinsames Diagramm.
Plot2:= plot(cos(x), x = -Pi..Pi, color = blue):
display([Plot1, Plot2]);
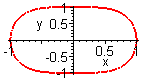
zeichnet gemäß der Gleichung Gl ein zweidimensionales Diagramm.
x = -1..1,
y = -1..1,
numpoints = 6000);
zeichnet die Punkte P1, P2, usw. in ein zweidimensionales Diagramm.
pointplot(Pkte, view = [0..5, 0..2]);
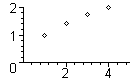
zeichnet ein Polygon, bzw. mehrere Polygone.
polygonplot(Fig, view = [0..5, 0..5]);
schreibt den Text Txt an der Position [x,y] in ein Koordinatensystem.
view = [0..2, 0..2],
align = BELOW);
zeichnet eine dreidimensionale Schlauchgrafik.
radius = t^2 + 1],
[0, 0, t, t = 0..1,
radius = 1 - t^2]},
view = [-2..2, -2..2, -1..1],
orientation = [112, 107],
numpoints = 10,
tubepoints = 30);
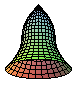
![]() Funktionen und Funktionsterme
Funktionen und Funktionsterme
![]() Konvergenz einer Folge
Konvergenz einer Folge
![]() Darstellungen einer Funktionenschar
Darstellungen einer Funktionenschar
![]() Funktionen von zwei Veränderlichen
Funktionen von zwei Veränderlichen
![]() Die Addition von Vektoren
Die Addition von Vektoren
![]() Flächen im Raum
Flächen im Raum
plottools
![]()
Elementare Grafikobjekte
with(plots):
with(plottools):
KoordSys ist ein mit plots[coordplot] definiertes Koordinatensystem.
definiert einen Kreisbogen mit dem Mittelpunkt M und dem Radius r.
a ist der Anfangs-, b ist der Endwinkel im Bogenmaß.
display({KoordSys, bg});
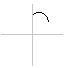
definiert einen Kreis mit dem Mittelpunkt M und dem Radius r.
display({KoordSys, kr});
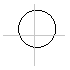
definiert eine farbige Kreisfläche mit dem Mittelpunkt M und dem Radius r.
kf2:= disk([1.9,0.9], .3, color = blue):
display({KoordSys, kf1, kf2});
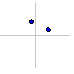
definiert eine Ellipse mit dem Mittelpunkt M;
rx und ry sind die Längen der Halbachsen.
el:= rotate(el, 2*Pi - 0.43):
display({KoordSys, el});
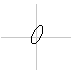
definiert eine Strecke mit dem Anfangspunkt (xa|ya) und dem Endpunkt (xb|yb).
display({KoordSys, li});

definiert ein Rechteck mit dem linken oberen Eckpunkt (x1|y1) und dem rechten unteren Eckpunkt (x2|y2).
display({KoordSys, rt});
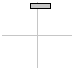

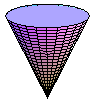
definiert einen Kegel mit dem Grundkreismittelpunkt M, dem Grundkreisradius r und der Höhe h.
cn:= cone(M, 2, 4):
display(cn, orientation = -44,74);
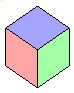
definiert einen Würfel.
P und Q sind die Endpunkte einer Raumdiagonalen des Würfels.
display(wf, style = patch);
definiert einen Zylinder.
M ist der Grundkreismittelpunkt, r der Grundkreisradius und h die Höhe des Zylinders.
zy:= cylinder (M, 2, 3):
display(zy,
style = patch,
scaling = CONSTRAINED,
orientation = [-170,65]);

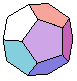
definiert einen Dodekaeder mit dem Mittelpunkt M.
display(dh, scaling = CONSTRAINED);
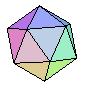
definiert einen Ikosaeder mit dem Mittelpunkt M.
display(ic, scaling = CONSTRAINED);
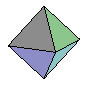
definiert einen Oktaeder mit dem Mittelpunkt M.
display(oc, scaling = CONSTRAINED
orientation = [18,-106]);
definiert eine Kugel mit dem Mittelpunkt M und dem Radius r.
display(kg, scaling = CONSTRAINED);

definiert einen Tetraeder mit dem Mittelpunkt M.
display(tr, scaling = CONSTRAINED);

student
![]()
Spezielle Prozeduren für den Mathematikunterricht;
inzwischen ersetzt durch das Package Student.
with(plots):
with(student):
rechnet das gegebene Polynom um in einen Ausdruck der Form a(x+b)2+ c.
completesquare(pol);
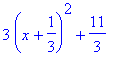
gibt den entsprechenden Ausdruck in mathematisch üblicher Schreibweise aus.
value(%);
gibt den entsprechenden Ausdruck in mathematisch üblicher Schreibweise aus.
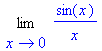
value(%);
1
Limit (cos(x)/x, x = 0);
undefined
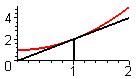
zeichnet das Schaubild von f und die Tangente an das Schaubild an der Stelle x0.
color = [black,red],
thickness = 2);
berechnet das Integral von f(x) in den Grenzen a und b nach der Simpsonregel.
n ist die Anzahl der benutzten Rechtecke.
evalf(%, 4);
2.418
berechnet das Integral von f(x) in den Grenzen a und b nach der Trapezregel.
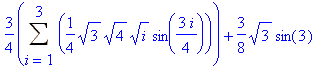
evalf (%, 4);
2.326
definiert eine Folge von n Rechtecken, deren linke obere Eckpunkte auf dem Schaubild einer Funktion f liegen.
Schaubild:= plot(x^2, x = 0..1):
display(Schaubild, LB);
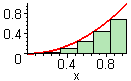
definiert eine Folge von n Rechtecken, bei denen die oberen Endpunkte ihrer Mittellinien auf dem Schaubild einer Funktion f liegen.
Schaubild:= plot(x^2, x = 0..1):
display(Schaubild, MB);
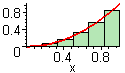
definiert eine Folge von n Rechtecken, deren rechte obere Eckpunkte auf dem Schaubild einer Funktion f liegen.
Schaubild:= plot(x^2, x = 0..1):
display(Schaubild, RB);
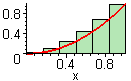
liefert die Summe der Flächeninhalte aller durch leftbox (f(x), x = a..b, n) gegebenen Rechtecke.
0.256
liefert die Summe der Flächeninhalte aller durch middlebox (f(x), x = a..b, n) gegebenen Rechtecke.
0.332
liefert die Summe der Flächeninhalte aller durch rightbox (f(x), x = a..b, n) gegebenen Rechtecke.
0.423
![]() Näherungsweise Bestimmung von Pi
Näherungsweise Bestimmung von Pi
![]() Das Simpsonverfahren
Das Simpsonverfahren
Student
![]()
Spezielle Prozeduren für den Mathematikunterricht
with(Student[Precalculus]):
rechnet das gegebene Polynom um in einen Ausdruck der Form a(x+b)2+ c.
CompleteSquare(pol);
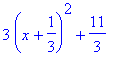
berechnet den Schwerpunkt eines Punktensembles.
CenterOfMass(pkte);
berechnet den Abstand zwischen den Punkten (a|b) und (c|d).
Line ([a,b], m);
liefert die zugehörige Geradengleichung, den Steigungsfaktor, den y- und den x-Achsenabschnitt.
Line([1,2], 3/2);
berechnet den Mittelpunkt zwischen den Punkten (a|b) und (c|d).
[3,4]
berechnet die Steigung der Geraden durch die Punkte (a|b) und (c|d).
5
with(Student[Calculus1]):
berechnet das Integral von f(x) in den Grenzen a und b nach dem angegebenen Verfahren (lower, upper, trapezoid, simpson, boole und andere).
Mögliche Werte für output: value, sum, plot, animation.
ApproximateInt(f(x),
x= 0..3,
method = simpson):
evalf(%, 4);
2.417
ApproximateInt(f(x),
x = 0..3,
method = trapezoid,
output = sum,
partition = 4):
simplify(%);
evalf(%, 4);
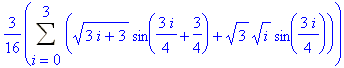
2.325
zeichnet das Schaubild von f und f ’.
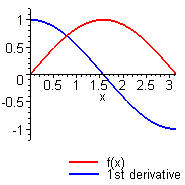
liefert den Mittelwert einer Funktion auf dem Intervall [a,b].
![]()
zeichnet das Schaubild von f unter Berücksichtigung besonderer Eigenschaften von f.
x = -3..3,
title = "",
slope = color(blue, red),
concavity = [],
pointoptions = [symbolsize = 15, color = black]);
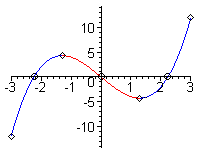
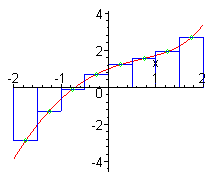
berechnet Riemannsummen bzw. zeichnet die zugehörigen Diagramme.
x = -2..2,
method = midpoint,
output = plot,
partition = 8,
title = "",
showarea = false);
![]() Numerische Berechnung eines Integrals
Numerische Berechnung eines Integrals
