dh-Materialien
Maple   Übungen

Die Fibonacci-Zahlen

> restart; with(plots):

Definition der Folge der Fibonacci-Zahlen mit Hilfe der Prozedur fib:

> fib:= proc(j)
  if j < 2 then j else fib(j-1) + fib(j-2) fi
end:

Berechnung und Ausgabe der ersten zwölf Fibonacci-Zahlen:

> fibonacci:= array(1..12):
for j to 12 do fibonacci[j]:= fib(j) od:
print(fibonacci);

fibonacc1 

Definition der Folge (fn ) der Fibonacci-Brüche:

> f:= n -> fib(n+1)/fib(n);

> print(seq(f(n), n = 1..12));

Definition der Differenzenfolge (dn ):

> d:= n -> f(n+1) - f(n);

> print(seq(d(n), n = 1..12));

(dn ) ist dem Anschein nach eine oszillierende, stark konvergierende Nullfolge:

> plot([seq ([n,d(n)], n = 1..12)], 
  color  = red,
  style  = point,
  symbol = circle,
  font   = [COURIER, 12],
  size   = [350, 350]);

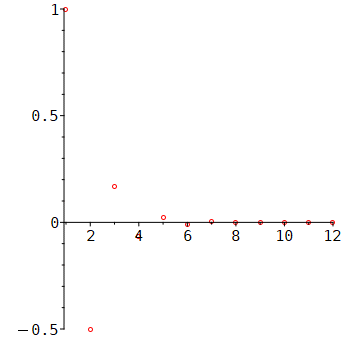
Unter der nahe liegenden Annahme, dass  (fn)  konvergent ist und den von 0 verschiedenen Grenzwert g besitzt, lässt sich wie folgt rechnen:

(fn) = (..., N/Z−N, Z/N, N + Z/Z, ... )  mit  limn→∞fn = g   und

> gl:= Z/N + (N+Z)/Z = 2*g;

gl := Z/N+(N+Z)/Z = 2*g

> gl:= expand(gl, Z/N);

gl := Z/N+1/Z*N+1 = 2*g

> gl:= subs(Z/N = g, N/Z = 1/g, gl);

gl := g+1/g+1 = 2*g

> gl:= factor(gl);

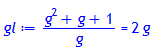
gl := (g^2+1+g)/g = 2*g

> gl:= (gl*g);

gl := g^2+1+g = 2*g^2

> gl:= lhs(gl) - g^2 = rhs(gl) - g^2;

gl := 1+g = g^2

> lgn:= solve(gl, g);

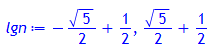
fibonacc22 

lgn[1] ist negativ, also:

> g:= lgn[2];

fibonacc23 

Die Folge (fn ) konvergiert also gegen die goldene Zahl (→ Mathematische Begriffe, Kapitel Verhältnis, Abschnitt Der goldene Schnitt).