Umkehrfunktion
definiert in: Funktion/ Umkehrfunktionen
Sei D eine Teilmenge von ℝ und f eine injektive Funktion von D nach ℝ. Dann gibt es zu jedem y ∈∈ f(D) ein x ∈∈ D mit f(x) = y und dieses x ist eindeutig bestimmt. Aus diesem Grund lässt sich die folgende Definition formulieren:
Sei D eine Teilmenge von ℝ und f eine injektive Funktion von D nach ℝ. Dann heißt die Funktion von f(D) nach D, welche jedem y ∈∈ f(D) das x ∈∈ D mit f(x) = y zuordnet, die Umkehrfunktion von f (oder die zu f gehörige inverse Funktion). Die Umkehrfunktion von f wird mit f−1 bezeichnet.
Die Umkehrfunktion einer Funktion f ist offenbar injektiv und es gilt (f−1)−1 = f sowie (f−1◦f)(x) = x und (f◦f−1)(y) = y für jedes x ∈∈ D bzw. jedes y ∈∈ f(D). Hierbei bedeuten f−1◦f und f◦f−1 die Verkettung von f mit f−1 bzw. von f−1 mit f.
Die Funktion f von ℝ+ nach ℝ mit f(x) = x2 ist streng monoton wachsend, also injektiv. f(ℝ+) = ℝ+. Ihre Umkehrfunktion f−1 ist für y ∈∈ ℝ+ gegeben durch f−1(y) = +√y. Das Schaubild einer solchen Umkehrfunktion erhält man durch Spiegelung des Schaubildes der Ursprungsfunktion an der Geraden y = x, sofern die Koordinatenachsen identisch skaliert sind:
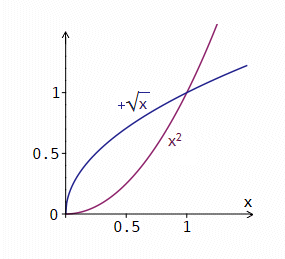
→ stetig → differenzierbar → Index
