Konstanten und Umgebungsvariablen
Folge von Bezeichnern aller von Maple vorgegebenen symbolischen Konstanten.
> constants;
Als Maple-Inputs geschrieben: false, gamma, infinity, true, Catalan, FAIL, Pi
Symbolische Konstante, die den Wahrheitswert true repräsentiert.
> type(true, symbol);
true
Symbolische Konstante, die den Wahrheitswert false repräsentiert.
> type(false, symbol);
true
Symbolische Konstante innerhalb der 3-wertigen Logik neben true und false.
> type(FAIL, symbol);
true
Rechenanweisungen, die zwar syntaktisch korrekt, aber mathematisch sinnlos sind, werden mit der Maple-Ausgabe
FAIL quittiert:
> degree(2^x, x);
FAIL
Wahrheitsfunktionen
Ausdruck vom Typ extended_numeric als Maple-Ausgabe bei
Rechenanweisungen, die zwar syntaktisch korrekt, aber aus mathematischen
Gründen kein Ergebnis liefern können.
> whattype(undefined);
extended_numeric
> with(RealDomain):
sqrt(-1);
undefined
Umgebungsvariable, die bestimmt, mit welcher Genauigkeit Maple
Berechnungen mit Gleitkommazahlen durchführt. Voreingestellter Wert für
die Integer-Variable Digits ist 10.
> type(Digits, integer);
true
Umgebungsvariable, die bestimmt, bis zu welcher Ordnung
Reihenentwicklungen berechnet werden. Voreingestellter Wert für die
Integer-Variable Order ist 6.
> type(Order, integer);
true
> series(sin(x), x = 0);
> Order:= 8;
series(exp(x), x = 0);
Es ist auch möglich, den Grad der Reihenentwicklung beim Aufruf der
Funktion series als Parameterwert anzugeben. Die entsprechende
Rechenanweisung würde für das letzte Beispiel wie folgt aussehen:
> series (exp(x), x = 0, 8);
Taylorreihen
Symbolische Konstante zur Darstellung der Kreiszahl
π.
> type(Pi, symbol);
true
Archimedes (287−212 v.Chr.) fand bei der Approximation des Kreises durch
ein 96-Eck den Näherungswert 3+10/71 mit einem Fehler von etwa 0,024%.
> evalf(100*(Pi - (3+ 10/71))/Pi);
0.02379633779
Von dem chinesischen Astronomen Ch’ung Chi Tsu (5. Jh. n. Chr.) stammt der
Näherungswert 355/113. Die Rechnung, die zu diesem Wert führte, ist bis heute unbekannt.
> evalf(100*(Pi - (355/113))/Pi);
Der holländische Mathematiker Ludolf van Ceulen (1540−1610) berechnete
die zunächst nach ihm benannte Ludolf’sche Zahl nach dem
Verfahren von Archimedes bis auf 35 Stellen genau.
> evalf(Pi, 35);
Vom englischen Mathematiker John Wallis (1616−1703) stammt folgende Formel:
> wallis:= n ->
4*Product(((2*i+1)^2-1)/(2*i+1)^2, i=1..n);
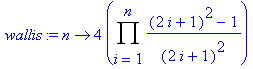
> wallis(100000);
3.141600508
Gottfried Wilhelm Leibniz (1646−1716) hat
π mit Hilfe einer Reihe berechnet:
> leibniz:= n -> 4*Sum((-1)^(i+1)/(2*i-1), i=1..n);
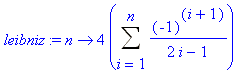
> value(leibniz(infinity)));
> evalf(leibniz(100000));
3.141582654
Von Leonhard Euler (1707−1783) ist die folgende 1736 gefundene Formel überliefert:
> pi[Euler]:= n -> sqrt(6*Sum(1/i^2, i = 1..n));
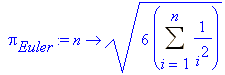
> evalf (pi[Euler](100000));
3.141583105
1882 wurde von Carl Louis Ferdinand von Lindemann (1852−1939) bewiesen, dass
π
nicht nur eine irrationale Zahl, sondern eine transzendente Zahl ist.
Das bedeutet: es gibt keine algebraische Gleichung mit rationalen
Koeffizienten und mit
π als Lösung.
Mit dem Computer ENIAC war es 1949 möglich,
π mit einer
Genauigkeit von 2000 Stellen zu berechnen (Rechenzeit: 70 Stunden). Die
Brüder Gregory und David Chudnovsky brachen 1989 in New
York die Milliardengrenze: 1001196691 Nachkommastellen von
π (Rechenzeit: 3 Tage mit der Maschine
IBM-ES/3090).
Yasumasa Kanada (Universität
von Tokio) veröffentlichte Ende 1999 seine mit der CPU HITACHI SR8000 in
37,5 Stunden berechneten
206.158.430.000 Dezimalstellen der Kreiszahl
π.
Am 31.12.2009 berechnete
Fabrice Bellard
mit einem einzelnen Desktop-PC in mehr als hundert Tagen über 2,7·1012 Dezimalstellen der
Kreiszahl.
Ein neuer Weltrekord wurde am 2. August 2010 von Alexander J. Yee und
Shigeru Kondo aufgestellt:
5 Trillion Digits of Pi
- fünf Billionen Dezimalstellen in 90 Tagen! Yee schrieb hierfür das Programm, Kondo baute den zugehörigen Rechner.
Im Dezember 2013 haben Yee und Kondo ihren eigenen Rekord noch übertroffen:
12.1 Trillion Digits of Pi.
Für ihren Algorithmus zur Berechnung der Nachkommastellen von haben Yee
und Kondo die Formel von Chudnovski verwendet:
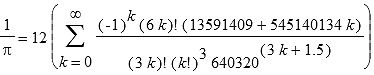
> evalf(Pi, 1000);
Symbolische Konstante zur Darstellung der Euler'schen Konstante.
> type(gamma, symbol);
true
Die Euler’sche Konstante (nicht zu verwechseln mit der Euler’schen Zahl e und üblicherweise auch mit
C bezeichnet) wird wie folgt berechnet:
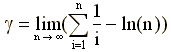
> evalf(limit(sum(1/i, i = 1..n) - ln(n), n = infinity));
0.5772156649
> evalf(gamma, 40);
Im Gegensatz zu e oder
π gibt es für
γ außer der oben hingeschriebenen Definitionsgleichung keine anderen
Darstellungen in einfacher Form.
Eine Verallgemeinerung der Definitionsgleichung für
γ liefert
Die Werte
γ(1),γ(2),
γ(3), ... stehen unter Maple als gamma(1), gamma(2), gamma(3), ... als Konstanten
zur Verfügung.
> type(gamma(1), constant);
true
> evalf(gamma, 1);
-0.07281584548
Symbolische Konstante zur Darstellung der Catalan’schen Konstante
> type(Catalan, symbol);
true
Die nach Eugène Charles Catalan (1814−1894) benannte Konstante Catalan ist wie folgt definiert:
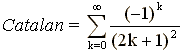
Es ist bis heute nicht bekannt, ob die Catalan’sche Konstante eine rationale oder eine irrationale Zahl ist.
> C:= Sum((-1)^k/(2*k+1)^2, k = 0..infinity):
evalf(C, 50);
evalf(Catalan, 50);
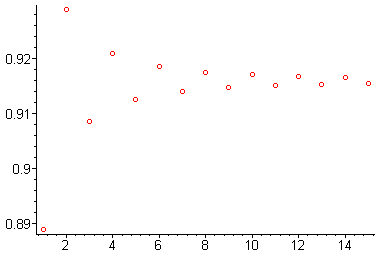
> C[n]:= Sum((-1)^k/(2*k+1)^2, k = 0..n):
for i from 1 to 15 do
print(evalf(subs(n = i, C[n])));
od:
> plot([seq([i, evalf(subs(n = i,
C[n]))], i = 1..15)],
style = point,
symbol = circle,
thickness = 3);
Konstante zur Darstellung der von Euler 1777 eingeführten komplexen Zahl i
(imaginäre Einheit).
> Complex(1);
I
> whattype(I);
complex(extended_numeric)
> solve(x^2 + 1 = 0, x);
I, -I
> exp(I*Pi);
-1
Rechnen mit komplexen Zahlen
Symbolische Konstante, die assoziiert ist mit dem mathematischen Begriff unendlich.
> type(infinity, symbol);
true
> infinity;
Eigenschaften der Konstanten infinity
NULL
Folge ohne Folgenglieder. Die Folge NULL vom Typ exprseq entspricht der leeren Menge
{ } vom Typ
set bzw. der leeren Liste [ ] vom Typ list.
> whattype(NULL);
exprseq
> folge:= NULL, a1, a2;
