Leonhard Euler

Leonhard Euler, geboren 1707 in Basel, gestorben 1783 in St. Petersburg.

Mit dem Namen dieses großen Mathematikers sind zahllose mathematische Dinge verbunden: der Euler’sche Polyedersatz, die Entdeckung des quadratischen Reziprozitätsgesetzes, die Herleitung der Exponentialreihe und der logarithmischen Reihe aus der binomischen Reihe, Methoden zur Lösung von Differentialgleichungen, die Euler’schen Kreiselgleichungen, ....

In seinen Arbeiten zur Differential- und Integralrechnung hat Euler Bezeichnungen und Symbole benutzt, die seitdem bis heute üblich sind: „π“ für die Kreiszahl, „e“ für die Euler’sche Zahl, „i“ für die imaginäre Einheit, „f(x)“ als Symbol für einen Funktionsterm, „Σ“ als Summenzeichen. Im 1748 erschienenen Werk Introductio in analysin infinitorum hat Euler die Formel veröffentlicht, die heute als Euler’sche Formel bezeichnet wird:

e^iφ= cos(φ) + i·sin(φ) für alle φ ∈∈ ℝ

Setzt man φ = π, so ergibt sich hieraus eine der schönsten mathematischen Gleichungen:

e^iπ+ 1 = 0.

Mit Hilfe der Euler’schen Formel ist es möglich, trigonometrische Funktionen als Linearkombination komplexer Exponentialfunktionen darzustellen.

Anwendung:
Jede lineare harmonische Schwingung genügt der Gleichung x(t) = A·cos(ωt + θ).
t steht hierbei für die Zeit, x(t) für die Elongation in Abhängigkeit von t, ω ist die Kreisfrequenz, A die Schwingungsamplitude, θ die Phasenverschiebung.

Unter Benutzung des Additionstheorems der Trigonometrie folgt
x(t)
= A·[cos(ωt)cos(θ) − sin(ωt)sin(θ)]
= A·cos(θ)·cos(ωt) + (−A·sin(θ))·sin(ωt).

Aufgrund der Euler’schen Formel ergibt sich mit a = A/2 unter Beachtung von i² = −1

x(t) = a·(e^iθ·e^iωt + e^−iθ·e^−iωt).

Rechentechnisch sind solche Exponentialfunktionsterme erheblich einfacher und übersichtlicher zu handhaben als trigonometrische Terme.

Eines der unzähligen Probleme, mit denen Euler sich beschäftigt hat, ist als Königsberger Brückenproblem bekannt: Gibt es einen Weg über die sieben Brücken in Königsberg derart, dass man auf diesem Weg jede der Brücken genau einmal überquert und genau dort wieder ankommt, wo man losgelaufen ist?

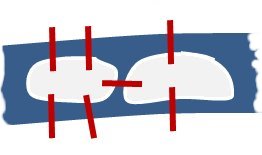
Sieben Brücken

Einen Weg mit den eben genannten Eigenschaften nennt man heute einen Euler’schen Weg und Euler hat 1736 bewiesen, dass es einen solchen Weg im hier dargestellten Beispiel nicht gibt.

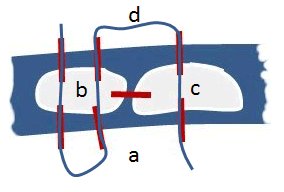
Wenn man die Gebiete, die durch die Brücken miteinander verbunden werden, mit a, b, c und d bezeichnet, dann definiert der Ausdruck [dbbaabbddcca] einen Weg, auf dem keine Brücke zweimal betreten wird, allerdings wird eine der Brücken garnicht betreten, also ist [dbbaabbddcca] ein unvollständiger Weg:

Sieben Brücken

Auch der Weg [abbddcca] ist unvollständig, aber geschlossen in dem Sinne, dass man in dem Gebiet endet, in welchem der Weg begonnen wurde:

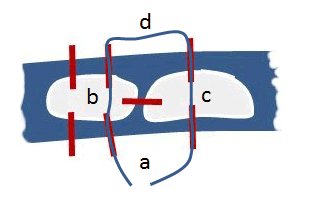
Sieben Brücken

Sowohl [dbbaabbddcca] als auch [abbddcca] sind jedenfalls zulässige Wege, was bedeutet, dass die jeweils nächste Brücke innerhalb eines Weges in genau dem Gebiet beginnt, in welchem die zuletzt benutzte Brücke geendet hat. Wenn ein Weg zulässig ist, dann kommen höchstens 2 der Bezeichner a, b, c und d in diesem Weg in ungerader Anzahl vor (dies sind diejenigen Bezeichner, die zum Startgebiet bzw. zum Zielgebiet gehören).

Angenommen, es gibt einen zulässigen und vollständigen Weg W über alle Königsberger Brücken, dann folgt zwingend wegen der Vollständigkeit von W, dass a 3 mal, b 5 mal, c 3 mal und d 3 mal in diesem Weg vorkommen müssen, das bedeutet, dass sogar alle 4 Bezeichner in W in ungerader Anzahl vorkommen. Hieraus folgt, dass W kein zulässiger Weg ist. Widerspruch!

Es existiert also kein zulässiger vollständiger Königsberger Weg und erst recht nicht ein zulässiger, vollständiger und geschlossener Weg.

1707	Euler wird am 15. April in Basel geboren.
1720	Immatrikulation an der philosophischen Fakultät der Universität Basel.
1724	Euler erhält die philosophische Magisterwürde.
1730	Physikprofessur an der Universität Sankt Petersburg (bis 1733).
1733	Mathematikprofessur an der Universität Sankt Petersburg (bis 1741).
1735	Anstellung im Geographischen Departement für kartographische Arbeiten.
1736	Euler entwickelt Newton’s Dynamik neu mit Methoden der damals neuen Differential- und Integralrechnung. Veröffentlichung von Mechanica sive motus scientia analytice exposita.
1741	Berufung von Euler an die Königliche Akademie der Wissenschaften in Berlin.
1744	Ernennung zum Direktor der mathematischen Klasse der Berliner Akademie. Lehrbuch zur Theorie der Bewegungen der Planeten und Kometen. Erste zusammenfassende Darstellung der Variationsrechnung.
1748	Veröffentlichung von Intraductio in analysis infinitesimorum (Einführung in die Analysis des Unendlichen).
1755	Veröffentlichung von Institutiones calculi differentialis (Darstellung der Differentialrechnung).
1760	Lettres à une princesse d'Allmagne (234 Briefe an die Brandenburgische Prinzessin Friederike, 1760−1762).
1766	Rückkehr nach Sankt Petersburg.
1768	Abhandlungen zur Integralrechnung: Institutiones calculi integralis.
1770	Lehrbuch der Algebra in deutscher Sprache: Vollständige Anleitung zur Algebra.
1783	Euler stirbt am 18. September.

Wikipedia: Leonhard Euler